К.ф.-м.н.,
доцент Габасова О.Р.
Белорусский
национальный технический университет
Об условиях ε-оптимальности программных управлений в задаче
оптимального управления одним типом гибридных систем
Рассмотрим линейную задачу оптимального
управления гибридных систем:
![]() , (1)
, (1)
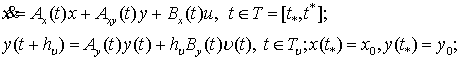 (2)
(2)
![]() , (3)
, (3)
![]() (4)
(4)
Здесь ![]() – промежуток
управления
– промежуток
управления ![]() ,
, ![]() фиксированы,
фиксированы, ![]() ,
, ![]() – периоды квантования
времени,
– периоды квантования
времени, ![]() – заданные натуральные числа
– заданные натуральные числа ![]() ,
, ![]() ;
; ![]() - заданные матрицы,
- заданные матрицы, ![]() ;
; ![]()
![]() ;
; ![]()
![]() ;
; ![]() ,
, ![]() – заданные матрицы и векторы;
– заданные матрицы и векторы; ![]() ,
, ![]()
![]()
![]() – заданные кусочно-непрерывные матричные функции.
– заданные кусочно-непрерывные матричные функции.
Определение.
Функция ![]() называется дискретной
в прямом (обратном) времени с периодом
называется дискретной
в прямом (обратном) времени с периодом ![]() заданное натуральное число), если
заданное натуральное число), если ![]()
![]()
![]()
Пусть ![]() ,
, ![]() ,
, ![]() – заданные дискретные матричные функции в прямом времени с
периодом квантования
– заданные дискретные матричные функции в прямом времени с
периодом квантования ![]() ;
; ![]() – дискретная функция в прямом времени с периодом квантования
– дискретная функция в прямом времени с периодом квантования ![]() ;
;![]() – состояние непрерывной части системы в момент времени
– состояние непрерывной части системы в момент времени ![]() ,
, ![]() – состояние дискретной части системы.
– состояние дискретной части системы.
Для задачи (1) – (4) справедлива следующая
формула Коши [1]:
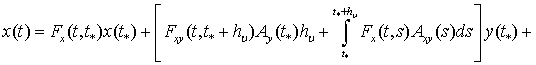
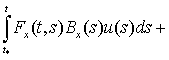
![]() (5)
(5)
![]()
![]() .
.
Здесь функции ![]()
![]() удовлетворяют
следующим условиям:
удовлетворяют
следующим условиям:
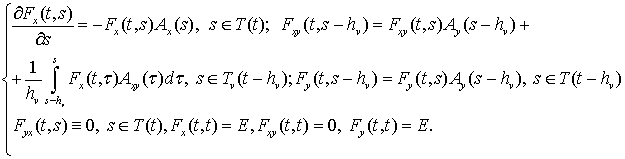 При построении
алгоритмов вычисления оптимальных программ большую роль играет оценка
субоптимальности
При построении
алгоритмов вычисления оптимальных программ большую роль играет оценка
субоптимальности ![]() , которая зависит от программы
, которая зависит от программы ![]() и опоры. Известно,
что при оптимальном управлении объектами, поведение которых описывается
обыкновенными дифференциальными уравнениями
и опоры. Известно,
что при оптимальном управлении объектами, поведение которых описывается
обыкновенными дифференциальными уравнениями
![]()
![]() , (6)
, (6)
оценка субоптимальности ![]() допускает разложение
допускает разложение
![]() ,
,
где ![]() -мера неоптимальности допустимой программы
-мера неоптимальности допустимой программы ![]() ,
, ![]()
![]() - мера неоптимальности опоры
- мера неоптимальности опоры ![]()
![]() - оптимальная программа, двойственная по отношению к задаче (5).
- оптимальная программа, двойственная по отношению к задаче (5).
Теорема 2. Оценка субоптимальности
опорного управления![]() допускает представление
допускает представление
![]()
![]()
![]() .
.
Доказательство.
Принимая во внимание результаты работы [3], запишем оценку субоптимальности
опорной программы для исходной задачи (1) – (4). Имеем
![]()
![]() . (7)
. (7)
Преобразуем (7):
![]()
![]()
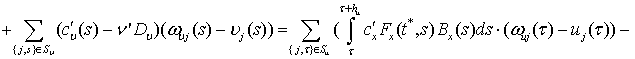
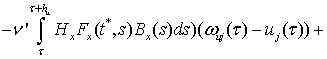 (8)
(8)
![]()
![]()
![]() .
.
Используя (5), получаем
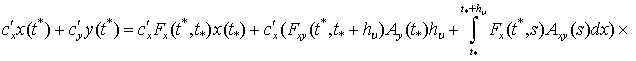
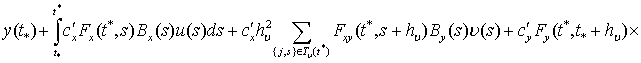
![]() (9)
(9)
Аналогично,
![]() æu
æu![]() +
+![]() æv
æv![]()
![]()
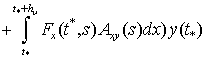
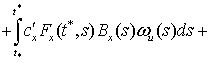 (10)
(10)
![]()
![]()
![]() .
.
Вычитая (9) из (10), получим
![]() æu
æu![]() +
+![]() æv
æv![]()
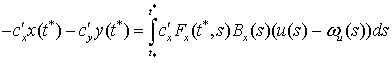 + (11)
+ (11)
![]()
![]() .
.
Проведем аналогичные преобразования ограничений (3)
![]()
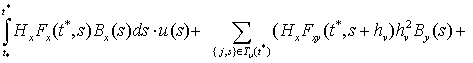
![]() (12)
(12)
![]()
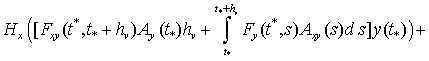
![]() .
.
![]() æu
æu![]() +
+![]() æv
æv![]() =
=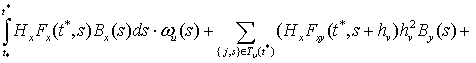
![]()
Сравнивая (12), (11) и (7) получаем
![]()
=![]() æu
æu![]() +
+![]() æv
æv![]()
![]() .
.
Теорема доказана.
Теорема 2
(критерий субоптимальности). При ![]() для
для ![]() -оптимальности программы
-оптимальности программы ![]() необходимо и достаточно существование такой опоры
необходимо и достаточно существование такой опоры ![]() , при которой на опорной программе
, при которой на опорной программе ![]() и соответствующих ей
траекториях
и соответствующих ей
траекториях ![]() ,
, ![]() прямой и сопряженной систем и котраектории
выполняются соотношения
прямой и сопряженной систем и котраектории
выполняются соотношения
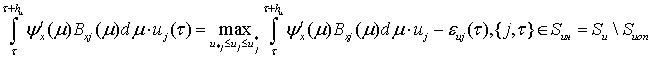
![]() ;
;
![]() .
.
Литература
1.Габасова О.Р.
Оптимизация линейных гибридных систем управления // Вестник БНТУ. –2007. – №
2. – С. 71 – 75.
2.
Альсевич В.В. Оптимизация линейных экономических моделей. Статические задачи:
учебное пособие / В.В. Альсевич, Р. Габасов, В.С. Глушенков– Мн.: БГУ, 2000. –
210 с.
3.
Конструктивные методы оптимизации в 5 ч. / Габасов Р. [и др.] Мн.: Университетское.
1984 – 1998. – Ч.1. Линейные задачи. Р.
Габасов, Ф.М. Кириллова, А.И. Тятюшкин – 1983. – 214 с.