Мустахаева
В.М., Акишев Г.
Институт
прикладной математики КН МОН РК, г. Караганда
Обобщение теоремы Марцинкевича-Зигмунда и неравенство разных метрик
Пусть 
и числа 
Через 
обозначим
пространство измеримых по Лебегу функций 
определенных на 
, для которых
,
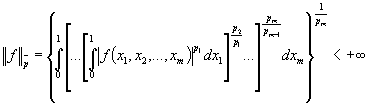где 
(см.[1], [2]).
Пусть 
. Рассматривается
ортогональная система 
удовлетворяющая условию
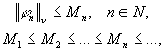
Рассмотрим кратную систему 
и ряд Фурь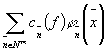е 
, где 
- коэффициенты
Фурье функции 
по кратной
ортогональной системе 
. Через 
обозначим
положительную величину зависыщий от указанных параметров.
Для функции одной переменной
Марцинкевичем и Зигмундом [3] доказаны следующие утверждения.
Теорема А ([3]). Пусть 
и 
. Тогда для функции 
справедливо
неравенство
.
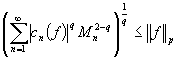Теорема
Б([3]). Пусть 
. Если ряды
, 
сходятся, то существует функция 
такая, что 
будут
коэффициентами Фурье по системе 
и
.
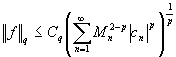Обобщение теорем А и Б на пространства
Орлича доказал Маслов А.В [4]. Усиление этих теорем установил В.И.Коляда [5].
Докажем двумерный вариант
теорем А и Б в пространстве 
со смешанной
нормой.
Теорема 1. Пусть
ортогональная система 
удовлетворяет
условию 
. Пусть 
, 
и 
, 
. Тогда
.
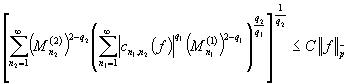Доказательство. Положим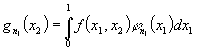 
. Тогда
.
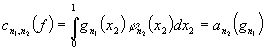При фиксированном 
применяя
теорему А получим
.
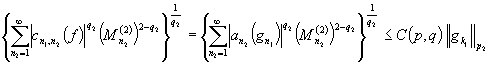Далее , пользуясь этой оценкой
имеем
. 
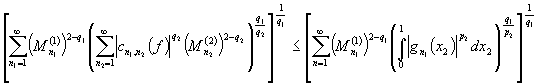По условию 
, а из этого следует, что 
. Таким образом 
.Поэтому в силу обобщенного неравенства Минковского
(см.[1], [2]) справедливо неравенство
.
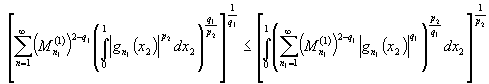Следовательно , из неравенства 
получим
. 
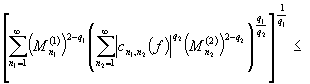
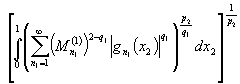Теперь снова пользуясь теоремой А
имеем
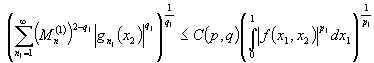
при фиксированном 
. Из неравенств 
и 
следует , что
. 
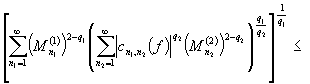
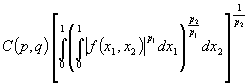Если 
, то 
. Поэтому пользуясь обобщенным неравенством Минковского
(см.[1], [2]) получим
.
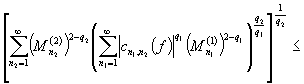
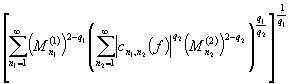Поэтому из оценки 
получим
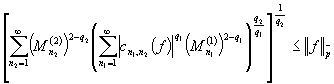
в случае
.Теорема доказана.
Теорема 2.
Пусть ортогональная система 
удовлетворяет
условию 
и 
, 
, 
, 
. Если ряды
,
,
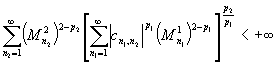то
существует 
такая, что
числа 
будут её
коэффициентами Фурье по системе 
и
.
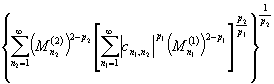Доказательство.
Пусть 
, 
ортонормированная система и выполняется
условие 
. Тогда по теореме Рисса-Фишера существует 
такая, что
числа 
будут
коэффициентами Фурье этой функции по системе 
.
Известно, что для функции 
справедливо
равенство
, 
, 
.
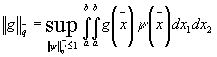Далее, пользуясь этим
равенством и теоремой 1, учитывая условия (6) можно убедиться в справедливости
утверждения теоремы 2.
Используя теоремы 1 и 2
докажем неравенство разных метрик для
полинома 
.
Неравенство
разных метрик для тригонометрических полиномов в пространстве 
доказано С.М.Никольским [1]. В дальнейшем оно обобщено различным авторами (см.
библиографию в [6] – [10] ).
Теорема 3. Пусть ортонормированная 
удовлетворяет
условию 
и 
или 
. Тогда для любого полинома 
выполняется неравенство
.
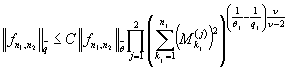Доказательство. По теореме 2 имеем
. 
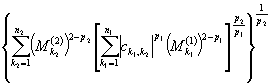Так как 
, то 
. Поэтому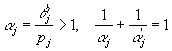 
. Теперь применяя неравенство Гельдера из формулы из
формулы 
получим
.
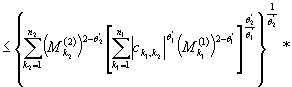
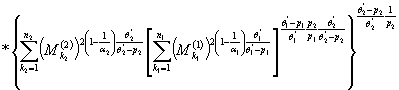Поскольку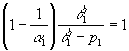 
, 
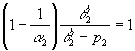и пользуясь теоремой
1 отсюда получим
.
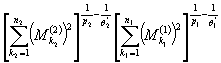Так как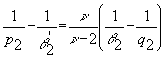 
, 
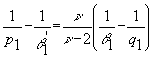, то из последнего неравенства получим утверждение
теоремы в случае 
т.е.
.
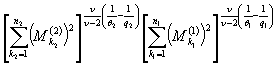Пусть 
Тогда 
. Теперь применяя равенство Парсеваля, неравенство
Гельдера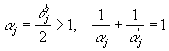 
и теорему 1 будем иметь
.
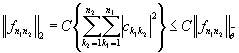
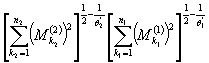Так как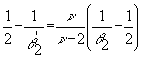 
, 
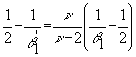, то
. 
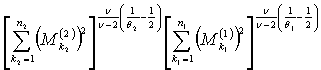Этим теорема доказана в случае 
Пусть 
. Тогда воспользуемся известным неравенством ([11],
стр. 176)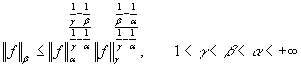 
. В этом неравенстве полагая 
будем иметь
.
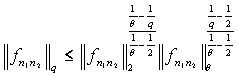Теперь пользуясь неравенством 
при 
получим
.
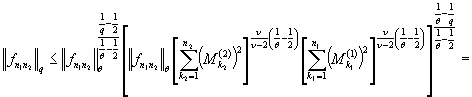
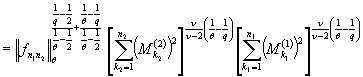Теорема доказана.
Замечание.
В одномерном случае аналог теоремы 3 доказан в [12].
Литература:
1.
Никольский
С.М. Приближение функций многих переменных и теоремы вложения, Наука, М., 1977
2.
Аманов Т.И.
Пространства дифференцируемых функций с доминирующей смешанной производной.
Алма- Ата, 1976, 224 с.
3. Marcinkiewicz
J., Zygmund A. Some theorems on orthogonal systems // Fund. math., 1937,
vol.28, p. 309-335
4.
Маслов А.В.
К вопросу об окончательности оценок для коэффициентов Фурье по общим
ортонормированным системам // Изв. вузов. Матем. 1985, №8, С.23-34.
5. Коляда В.И. О некоторых обобщениях теоремы
Харди – Литлльвуда – Пэли. Матем. заметки , 1992, т. 51, № 3, С.24 – 34.
6.
Nessel R.J., Wilmes G. Nikol’skii type inequalities
for trigonometric polynomials and entire functions exponential type. Journal Austral. Math. Soc., ser. A, 1978, v. 25, № 1, P. 7 – 18.
7.
Смаилов Е.С.
О влиянии гоеметрических свойств спектра многочлена на неравенства разных
метрик С.М. Никольского. Сиб.мат.журнал 1998, т.39, №5, С.1157-1163.
8.
Унинский
А.П. Неравенства в смешанной норме для тригонометрических полиномов и целых
функций конечной степени. Труды
всесоюзного симпозиума по теоремам вложения. , Баку , 1966, с. 212 – 218.
9.
Акишев Г.
Неравенства разных метрик для полиномов в пространстве Лоренца со смешанной
нормой. Материалы международной научной конференции «Первые Ержановские
чтения», Павлодар, 2004, т. 2, С. 211 – 215.
10. Нурсултанов Е. Д. Неравенства разных метрик С.М. Никольского и
свойства последовательностей норм сумм Фурье функции из пространства Лоренца.
Труды математического института им. В.А. Стеклова – 2006 – Т. 255 – С. 1 – 18.
11. Харди Г. Г., Литтльвуд Д.Е., Полиа Г.. Неравенства. М. 1948. 456
с.
12.
Мустахаева В.М., Акишев Г. Неравенство разных
метрик для полиномов по ортонормированным системам. Материалы 2-ой
республиканской научно-практической конференции «Молодежь и наука в современном
мире», Талдыкорган, 2010, С. 95-97.