Ткаченко О.С.

Загальноосвітня школа І-ІІІ ступенів № 4 м.Красноармійська, Україна

Застосування показникової функції, чи «Оди експоненті» .

Більшість процесів у житті пов’язано із залежністю між величинами. Наприклад, кількість виконаної роботи залежить від її обсягу та складності самої роботи, рівень знань учня від рівня його інтелектуального розвитку вартість покупки від кількості купленого товару і цін. Одна залежність носить випадковий характер, інші постійні. Розглянемо різноманітні процеси, які проходять в природі.

Радіоактивний розпад. Під час радіоактивного розпаду маса m речовини змінюється на протязі часу t по закону: m =m₀ a^kx , де m ─ маса речовини через t років після початку розпаду; m₀ ─ початкова маса речовини; k и a ─ постійні величини для даної речовини.

Приріст населення. Кількість y жителів міста З мільйонним населенням через x років обчислюється за формулою y = 1 000 000 • 1,02^x (при умові, що кожного року спостерігається приріст населення на 2%).

Зміна температури. Температура Т 100 г піску, нагрітого до 100ºС, зміняються при 0ºС в залежності від часу t за формулою: Т = 100 • 0,8 ^{t .}

Зміна рівня рідини. Під час витікання рідини з циліндричної посудини через тонку трубку, розміщену в основі циліндра, висота h рівня рідини із зміною часу t змінюється по формулі: h=h₀ а^t, де h₀ ─ початковий рівень рідини ; a ─ постійна, яка залежить від діаметра трубки.

Зміна атмосферного тиску. Атмосферний тиск змінюється в залежності від висоти h над рівнем моря за законом p = p₀ a^h ,де p ₀ ─ атмосферний тиск над рівнем моря; a ─ постійна величина.

Розмноження бактерій. Розмноження бактерій в деякому середовищі проходить так, що їх кількість Ν зміняється з часом за законом Ν = Ν ₀ a^kt, де N ₀ ─ початкова кількість бактерій при t = 0; a і k ─ постійні величини.

Приріст деревини. Дерево росте так, що кількість деревини з часом збільшується по закону М = М₀ a^kt , де М – кількість деревини у даний момент, м³; М₀ ─ початкова кількість деревини; t - час (в роках ), який відлічується з моменту, коли об`єм деревини був М₀; k ─ деяка постійна

Застусування показникової функції в фізиці.

Знання про показникові функцію є основою при вивченні таких тем, як "похідна exponential", " "термодинаміка", "Електромагнетизм", "Коливання".

При падінні тіл у безповітряному просторі їх швидкість рівномірно збільшується. Інакше відбувається падіння в повітрі. Вважаємо, що сила опору повітря пропорційна швидкості падіння, тобто (знак „мінус” показує, що напрям сили опору повітря направлений вбік, протилежний напряму падіння). Через t секунд після початку падіння швидкість , де m – маса парашутиста. Коли t збільшується, то зменшується і прямує до 0, вираз у дужках прямує до 1, , тобто падіння стане рівномірним; k залежить від густини повітря, площі поверхні тіла, що падає, тощо.

Наприклад, при падінні з парашутом цей коефіцієнт доволі великий, і тому швидкість приземлення парашутиста порівняно мала — 5 м/с. Ясно, що швидкість падіння пушинки буде меншою, ніж швидкість падіння свинцевої кульки, що має ту саму масу, бо пушинка має більшу площу поверхні і тому більше значення k. Саме тому пушинка так повільно опускається вниз і так легко підхоплюється потоком повітря. Аристотель у своїх міркуваннях не враховував опору повітря і вважав, що важкі тіла у стільки разів падають швидше за легкі, у скільки разів вони важчі за них. Галілей експериментально заперечив це твердження, кидаючи кулі з похилої Пізанської башти.

ЗАДАЧА: Розглянемо завдання про падіння парашутиста. Якщо вважати, що сила опору повітря пропорційна швидкості падіння парашутиста, тобто що F=kv , то через t секунд швидкість падіння дорівнюватиме: v=mg/k(1-e^-kt/m), де m - маса парашутиста. Через деякий проміжок часу е^-kt/m стане дуже малим числом, і падіння стане майже рівномірним. Коефіцієнт пропорційності k залежить від розмірів парашута. Дана формула придатна не тільки для вивчення падіння парашутиста, але і для вивчення падіння краплі дощової води, пушинки і т.д.

ЗАДАЧА: Якщо при коливаннях маятника, гирі, що гойдається на пружині, не нехтувати опором повітря, то амплітуда коливань стає все менше, коливання затухають. Відхилення точки, що здійснює загасаючі коливання, виражається формулою: s=Ae^{-ktsin(хt+х)}. Так як множник е^-kt зменшується з часом, то розмах коливань стає все менше і менше.

ЗАДАЧА. Радіоактивний розпад речовини задається формулою

m=m₀(),, де m і m₀ маса радіоактивної речовини у момент часу t і в початковий момент часу t=0; T - період напіврозпаду(проміжок часу, за який первинна кількість речовини зменшується удвічі). Коли радіоактивна речовина розпадається, його кількість зменшується. Через деякий час залишається половина первинної кількості речовини. Чим більше періоду напіврозпаду, тим повільніше розпадається речовина.

Завдання 1.

Період напіврозпаду плутонію Т=140 добам. Який стане маса m плутонію через 10 років, якщо його початкова маса m₀=8г?

  В даній задачі t=10365 (враховуємо, що в році 365 днів), =. За формулою радіоактивного розпаду, за допомогою калькулятора знаходимо m=8()1,1345 ^. 10^-7 .

Відповідь.

Через 10 років плутонія залишиться 1 вари.13 ^. 10^-7 г.

Завдання 2. При радіоактивному розпаді кількість деякої речовини зменшується вдвічі за добу. Скільки речовини залишиться від 250 г через : а) 1,5 діб; б) 3,5 діб?

а) m₀₌250г T=1 діб t=1,5 діб

m=m_{0 ()}^{1,5 .}m=250 *0,5=250 =25088,4(г).

б) m₀₌250г T=1 діб  t=3, 5 діб

m=m_{0 ()}^3,5. m=250 ∙0,5^7/2=250 = 250 ∙ 0 ,25 22,1(г).

Явище радіоактивного розпаду використовується для визначення віку археологічних знахідок, наприклад, визначений зразковий вік Землі(близько 5,5 млрд. років).

ЗАДАЧА. Зміна атмосферного тиску p залежно від висоти h над рівнем моря описується формулою p=p₀ a^k, де p₀- атмосферний тиск над рівнем моря, а - деяка постійна.

ЗАДАЧА. Усі, напевно, помічали, що якщо зняти киплячий чайник з вогню, то спочатку він швидко остигає, а потім охолодження йде набагато повільніше. Річ у тому, що швидкість охолодження пропорційна різниці між температурою чайника і температурою довкілля. Чим менше стає ця різниця, тим повільніше остигає чайник. Якщо спочатку температура чайника дорівнювала Т₀, а температура повітря Т₁, то через t сeкунд температура Т чайника виразиться формулою: Т = (Т₁-Т₀) е^{- кt} + Т₁, де до - число, залежне від форми чайника, матеріалу, з якого він зроблений, і кількості води, яка в ньому знаходиться.

ЗАДАЧА. При падінні тіл у безповітряному просторі швидкість їх безперервно зростає. При падінні тіл в повітрі швидкість падіння теж збільшується, але не може перевершити певної величини

ЗАДАЧА. Площа перерізу тросу пов’язана з опором розриву також за показниковим законом.

Зараз багато морів та океанів борознять дослідницькі кораблі. У заздалегідь встановлених місцях вони зупиняються і опускають за борт трос, на кінці якого знаходяться прилади. Їх опускають на дно, а потім піднімають вгору і записують показники. Але іноді відбувається неприємна подія - трос розривається і всі цінні прилади опиняються назавжди на дні моря.

Здавалось, що цієї проблеми можна було б уникнути, якщо зробити трос товщим. Але тут виникає нове ускладнення – верхні частини троса повинні утримувати не тільки прилади, які занурюють, але й нижню частину троса, тому при потовщенні троса на верхню частину ляже дуже велике навантаження.

Тому доцільно робити нижню частину тросу тоншою, ніж верхню. Виникає питання: як повинна змінюватись товщина тросу для того, щоб в будь якому перерізі його на 1 см² приходилась одне й те ж саме навантаження?

Досліди цього питання показали, що площа перерізу тросу повинна змінюватись за законом: , де

S₀ – площа нижнього перерізу,

S – площа перерізу на висоті х від нижнього перерізу,

γ – питома вага матеріалу, із якого зроблено трос,

Р – вага в воді вантажу, який опускають.

Такий трос називають тросом рівного опору розриву. Він має найменшу масу, ніж трос постійного перерізу, який розрахований на таке ж навантаження.

Показникова функція в теорії міжпланетних подорожей

Багато складних задач доводиться розв'язувати в теорії міжпланетних подорожей. Однією з них є задача про визначення кількості палива, необхідного для того, щоб надати ракеті швидкість υ₁, потрібну для досягнення Місяця, Венери, Марса або якоїсь іншої планети. Ця кількість залежить від маси m₀ самої ракети (без палива) і від швидкості υ_о, з якою продукти згоряння витікають із сопла ракетного двигуна.

К. Е. Ціолковський розглянув задачу про паливо, нехтуючи опором повітря і притяганням Землі.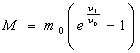

Для ракети масою 1,5 т щоб надати швидкість 8000 м/с, треба при швидкості закінчення газів 2000 м/с взяти приблизно 80 т палива.
Вихід знайшов С. Корольов, запропонувавши багатоступінчасті ракети.

До речі, вам цікаво буде знати, що всі названі четверо генеральних конструкторів ракетно-космічної техніки (С. Корольов, М. Янгель, В. Челемей і В. Глушко) — українці, а К. Ціолковський — прямий нащадок Северина Наливайка; його батько, Едуард Ціолковськлй, що мав подвійне прізвище Ціолковський-Наливайко, народився на Рівненщині, у селі Коростятин, мав родичів у Львові.

Показникові функція в банківській справі

Ще за стародавніх часів було широко поширене лихварство — віддавання грошей у позику під відсотки. Селянин у разі неврожаю, ремісник, майно якого знищила пожежа, розорений торгівець змушені були йти до лихваря, обіцяючи наступного року повернути суму значно більшу, ніж узята в позику. Наприклад, у Давньому Вавилоні лихварі брали по 20 % лихви на рік. При цьому, якщо боржник не міг повернути борг наступного року, йому треба було платити відсотки не тільки з позиченого капіталу, а й з відсотків, що виросли за рік. Тому через 2 роки слід було заплатити не 40 %, а 44 % лихви, адже 1,2² = 1,44. За 5 років сума боргу збільшувалася в 1,2⁵ разів, тобто майже в 2,5 рази, а за 10 – років більш ніж у 6 разів. Зрозуміло, що більшість боржників були не в змозі повернути борг і, давно виплативши основну суму боргу, були змушені все життя працювати на те, щоб виплатити все зростаючі відсотки. Нарешті зубожілі боржники ставали рабами хижого лихваря.

У XIV—XV ст. у Західній Європі почали з'являтися банки (від фр. banque — лава, контора) — установи, які давали гроші в позику князям та купцям, фінансували за великі відсотки далекі мандрівки та завойовницькі походи. Щоб полегшити розрахунки складних відсотків, склали таблиці, за якими відразу можна було дізнатися, яку суму треба виплатити через п років, якщо була взята сума а під p% річних. Легко підрахувати, що сума, яку треба заплатити, виражається формулою:

Якщо р — стале, то S є функцією від п. Такі таблиці давали значення показникової функції при різних значеннях основи і натуральних значеннях п.

Останнє обмеження було не дуже зручним: іноді гроші бралися в борг не на ціле число років, а, наприклад, на 2 чи 6 місяців. Так виникла ідея степеня з дробовим показником. Ця ідея належала ще Архімеду, але вона не була зрозумілою його сучасникам. І лише через 1,5 тисячоліття почали розглядати піднесення чисел до степеня з дробовим показником.

Показникова функція та інформаційний бум

Нині багато говорять про інформаційний бум. Стверджують, що кількість інформації подвоюється кожні десять років. Зобразимо цей процес у вигляді графіка деякої функції.

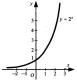
Візьмемо обсяг інформації в деякий початковий рік за 1. Удвічі більший відрізок поставимо над одиничною оцінкою, вважаючи, що оцінка відповідає першому десятку років. Удвічі більший відрізок відповідає другому десятку років, ще вдвічі більший — третьому і т.д. Обрані нами значення аргументу є елементами арифметичної прогресії: 1, 2, З, ... . У той самий час значення функції зростають за законом геометричної професії: 2, 4, 8, ... . Подивимося, який був обсяг інформації до року, прийнятого за початковий. По осі абсцис уліво від початку координат відкладатимемо значення функції в порядку зменшення — у 2 рази менше з кожним кроком. Сполучимо всі побудовані точки плавною лінією. Перед нами графік показникової функції. Головна особливість графіка цієї функції — її крутизна. Показникова функція зустрічається в описі процесів, у яких швидкість зміни величини пропорційна до самої величини.

Показникова функція у літературі

У романі Жуля Верна „Матіас Шандор” виведено образ силача Матіфу, який здійснив багато подвигів. Ось один із них.

Готувався спуск на воду корабля. І саме в цей момент до гавані влетіла яхта, яка неминуче врізалася б у корабель, якби з натовпу не вибіг чоловік, який з усієї сили вперся в землю ногами і вчепився в трос, що утримував корабель, щоб затримати спуск. Поблизу стояла гармата. Сміливець швидко накинув на неї трос і з нелюдським зусиллям утримував його 10 секунд, поки трос не лопнув. Але цих 10 секунд було досить, щоб яхта проскочила повз корабель — зіткнення не сталося. Звичайно, ви здогадалися, що сміливий незнайомець — це Матіфу.

Але чи потрібна нелюдська сила, щоб утримати корабель?

„Чи може людина втримати корабель?”

Згадаємо, як відбувається швартування корабля. З нього кидають канат на берег. Людина, що стоїть на пристані, обмотує кілька разів канат навколо стовпа. Сила тертя між канатом і стовпом і утримує судно.

Якщо F₀ — прикладена сила, F— сила, що утримує корабель, то маємо:

1 виток: F= F₀ • k;

2 витки: F= F₀ • к²,

3 витки: F= F₀ • k³,

..................................

x квитків: F= F₀ • k^x;

k залежить від матеріалу, з якого зроблено канат і стовп. Наприклад, коли канат —з конопель, а стовп залізний, то . Тобто, обернувши канат 3 рази, силою 22 Н можна утримувати 40 т

Показникова функція в біології

Розглянемо, як зростає популяція бактерій у відповідності з простим життєвим циклом. При цьому час між моментом поділу материнської клітини (народження нової) і моментом, коли вона сама ділиться, називається періодом поділу, або часом генерації.

ЗАДАЧА. Нехай число бактерій у культурі становить А₀. За час однієї генерації всі ці А₀ бактерій поділяться навпіл і утвориться 2А₀ бактерій. Через дві генерації їх стане 2 • 2А₀, через три — 2 • 2 • 2А₀ і т.д. Через р генерацій А = 2^Р • А₀.

Нехай час однієї генерації Т, тоді , де t час з початку розподілу. .

Бачимо, що популяція росте за показниковим законом, або, як кажуть, експоненціально (лат. exponense — той, хто показує).

Саме здатність бактерій до швидкого розмноження забезпечує їх кількісну перевагу серед живих форм. Якби не було природних причин, що заважали б вибухам кількості бактерій, сумарна маса яких становила б декілька десятків тисяч тонн, а за дві доби показникового зростання маса однієї бактерії перевищила б у декілька разів масу Земної кулі. Наша планета, проте, не перетворилася на суцільну масу мікробів. І це не тільки тому, що бактерії вичерпують поживні речовини, які підтримують їх зростання, а й тому, що при зростанні вони виділяють велику кількість продуктів, токсичних для них самих.

З відкриттям англійським мікробіологом Флемінгом пеніциліну і народженням нової промисловості знати кількість грибків, утворених у процесі розвитку, стало важливо і можливо при використанні виведеної раніше формули.

Звичайно, показниковий закон виконується дуже приблизно в біологічних системах, бо ми маємо тут справу з дуже складними системами.

ЗАДАЧА. За законом показникової функції розмножувалося б все живе на Землі, якби для цього були сприятливі умови, тобто не було природних ворогів і було вдосталь їжі. Доказ тому-поширення Австралії кроликів, яких там раніше не було. Досить було випустити пару особин, як через деякий час їх потомство стало національним лихом.

ЗАДАЧА. Якби всі макові зерна давали сходи, то через 5 років число "нащадків" однієї рослини дорівнювало б 243 • 10¹⁵ або приблизно 2000 рослин на 1 м суші.

ЗАДАЧА. Потомство кімнатних мух за літо тільки від однієї самки може скласти 8 • 10¹⁴. Ці мухи важили б кілька мільйонів тонн, а вибудувані в один ланцюжок, вони склали б відстань, більшу, ніж відстань від Землі до Сонця. Потомство пари мух за 2 роки мало б масу, що перевищує масу земної кулі. І тільки завдяки спільноті тварин і рослин, коли збільшення одного виду тягне за собою зростання кількості його ворогів, встановлюється динамічна рівновага в природі.

Показникова функція в медицині

Коли людина лякається, в кров виділяється адреналін, який потім руйнується, причому швидкість руйнування пропорційна кількості цієї речовини, що ще залишилася в крові.

При діагностиці хвороб нирок часто визначають здатність нирок виводити з крові радіоактивні ізотопи, причому їх кількість спадає за показниковим законом.

ЗАДАЧА. Швидкість зміни кількості ліків у організмі пропорційна їх кількості. Якщо А(t) — кількість ліків у тілі через час t, R₀ -швидкість надходження ліків до організму (стала — відома величина), k — коефіцієнт пропорційності (стала, що характеризує швидкість виведення ліків з організму), то

ЗАДАЧА. При відновленні концентрації гемоглобіну в крові донора або пораненого за показниковим законом спадає різниця між нормальним вмістом гемоглобіну і наявною кількістю цієї речовини. Як і при радіоактивному розпаді, лікарі розглядають період, за який розпадається або відновлюється половина речовини. Для адреналіну — частки секунди, для ізотопів — хвилини, для гемоглобіну — дні.

Звичайно, показниковий закон виконується дуже приблизно в біологічних системах, бо ми маємо тут справу з дуже складними системами.

ЗАДАЧА. Реакції організму на два види ліків як функції часу t (час виражено у годинах) складають r₁(t) =t_e^-t і r₂ (t) =t^-2 е^-t. У якого з видів ліків максимальна реакція вища? Ліки якого виду діють повільніше?

Про диференціювавши функції r₁(t) і r₂ (t), що визначені і неперервні на проміжку (0; ), і розв’язавши рівняння е^-t (1-t) = 0 і е^-t (2-t) = 0, з’ясуємо, що ці функції на вказаному проміжку мають по одній стаціонарній точці t₀₁=1; t₀₂=2. Оскільки в кожному з випадків при переході через стаціонарну точку знак похідної змінюється з “+” на “-“, то на підставі достатньої умови існування екстремуму в точці робимо висновок, що точка t₀₁=1 є точкою максимуму функції r₁(t), а точка t₀₂=2 є точкою максимуму функції r₂ (t).

Знайшовши максимуми функції r₁ (1)= 1/е0,37 і r₂ (t)=4/е² 0,54, з’ясуємо, що у другого виду ліків максимальна реакція вища і вони діють повільніше.

Дана задача, складена на підставі необхідної і достатньої умов існування екстремумів функції, може бути застосована для повторення або закріплення знань і формування вмінь використовувати ці теореми в нових умовах, що створюються прикладним змістом навчальної задачі. До того ж ця задача є прикладом одного з видів задач про знаходження найбільшого значення функцій.

Показникова функція в хімії

Ви усі чули про ланцюгові реакції, теорію яких в 20-х роках описав молодий хімік Н.Н. Семенов, а потім розвинули учені-атомники. Як управляти цим процесів в мирних цілях? На це питання можна відповісти тільки за допомогою знань про показову функцію.

ЗАДАЧА. Тиск атмосфери, виражений в міліметрах ртутного стовпа міняється згідно із законом: , де h - висота точки над рівнем моря(у м). Цю формулу використовують геодезисти для барометричного інвелірування, тобто для визначення різниці висот над рівнем моря двох точок на земній поверхні.

ЗАДАЧА . При проходженні світла через каламутне середовище кожен шар цього середовища поглинає строго певну частину світу, що падає на нього. Сила світла I визначається по формулі: I = I₀e^-ks, где: s - товщина шару, k - деякий коефіцієнт, що характеризує каламутне середовище. Подібний же закон характеризуватиме процес поглинання газу відповідним середовищем, зміну швидкості вітру і тому подібне.

ЗАДАЧА. Закон охолодження. Нехай Т₁ - температура тіла, Т₀ - температура довкілля, де Т₁>Т₀, Тоді температура тіла Т мінятиметься згідно із законом: Т = Т₀ + (Т₁ - Т₀) е^{- kt}, де k - деякий коефіцієнт, залежний від природи охолоджувального тіла. Приклад, процес охолодження розплавленого парафіну. Якщо коефіцієнт буде не відомий, то необхідно досвідченим шляхом упізнати температуру Т₂ в який-небудь момент часу t₂. Тоді: Т₂ = Т₀ + (Т₁ – Т₀)е^-kt, звідси знайдемо: 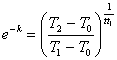Тоді: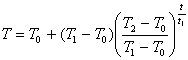

Ми ще раз переконалися, що математика — це всеосяжна наука, без знання якої неможливо ні пізнати оточуючий нас світ, ні забезпечити науково-технічний прогрес. Як казав великий Ейнштейн : „Природа – це реалізація найпростіших математичних ідей”.

Різноманітні застосування показникової (чи її ще називають, експоненціальною) функції надихнули англійського поета Елмера Голила на написання "Оди експоненті", уривок з якої свідчить:

"Нею породжено багато що з того, що "гідно згадки",

Як говорили наші англосакські предки.

Могутність її породжень

Заздалегідь обумовлено її власною красою і силою,

Бо вони суть фізичне втілення

Абстрактної ідеї є.

Англійські моряки люблять і знають її

Під ім'ям " Гунтер".

Дві шкали Гунтера - ось диво винахідливості.

Експонентою породжена логарифмічна лінійка: у інженера і астронома не було

Інструменту корисніше, ніж вона.

Навіть витончені мистецтва живляться нею.

Хіба музична гамма не є набір неперових логарифмів?

І таким чином щось абстрактне красиве стало предком одного з найбільших людських досягнень" 

Література:

1. Виленкин Н. Я. „Функции в природе и технике”, М., „Просвещение”,М.,1978.

2. Клейнер Г. М., Клейнер Л. М. Математическая и научная картина мира. — К..: Рад. шк., 1984.

3. Петрик М., Баб’юк М. Основи математичного моделювання та застосування математичних методів у наукових дослідженнях. —Тернопіль: Підручники і посібники, 1998.