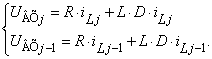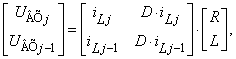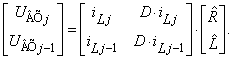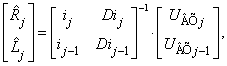Идентификация параметров динамического объекта первого порядка на основе разностных схем

Боловин Е.В.

Студент, Кафедра Электропривода и Электрооборудования, Национальный Исследовательский Томский Политехнический Университет, Томск, Россия

Реферат

В данной статье представлен метод идентификации динамических объектов первого порядка, разработанного на основе разностных схем.

Ключевые слова: динамический объект первого порядка, идентификация параметров, разностные схемы.

Введение

Современное производство не может обойтись без электропривода. В данных приводах применяются различные двигатели, как по структуре и назначению, так и по возрастной категории. Эффективное управление данными двигателями возможно лишь, если известны текущие значения их параметров. Но, зачастую определить параметры либо невозможно, либо крайне сложно. Это связано и с новыми импортными двигателями, где указана лишь мощность и частота вращения, и со старыми, проработавшими десяток лет, у которых паспортные данные, либо были потеряны, либо двигатель проходил не однократные ремонты. Соответственно, остро встает вопрос об идентификации их параметров.

Идентификация параметров динамического объекта первого порядка

Рассмотрим динамический объект первого порядка RL-цепь

Составим уравнение равновесия:

(1)

Произведем алгебраизацию дифференциального уравнения (1)

(2)

где – оператор дифференцирования.

Произведем дискретизацию уравнения (2), при этом значения входного напряжения и тока RL-цепи будут определены в моменты времени

(3)

где – интервал дискретизации или шаг по времени, j – номер шага по времени или при постоянстве это аргумент разностного уравнения, получаемого из (2)

(4)

Для идентификации двух параметров RL-цепи (сопротивление и индуктивность) составим систему линейных алгебраических уравнений (СЛАУ) на основе (4), состоящая из первого уравнения, когда и из второго уравнения при

(5)

Для реализации процедур идентификации параметров RL-цепи СЛАУ (5) необходимо представить в матричной форме следующего вида

(6)

здесь 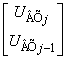– вектор входных в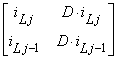еличин, – матрица выходных величин, – вектор параметров.

Составим математическую модель объекта, включающую оценки искомых параметров

(7)

Найдем оценки параметров по методу обратной матрицы

(8)

учитывая что – вектор оценки параметров на j-ом шаге, – первая левая разность на j-ом шаге, - время одного шага.

Заключение

Представлена процедура составления разностных уравнений для идентификации параметров динамических объектов первого порядка. Данная процедура может быть применена к двигателям с DSP-контроллерами.