УДК 628.218
ИДЕНТИФИКАЦИЯ ДИНАМИЧЕСКИХ ХАРАКТЕИСТИК ТЕПЛОГЕНЕРИРУЮЩИХ
ОБЪЕКТОВ ПО СЛУЧАЙНЫМ ВХОДНЫМ СИГНАЛАМ
Кулешова Э.И., д.т.н.,
проф. Гусенцова Я.А., Гущин А.А.
Луганский национальный
аграрный университет
к.т. н., проф. Коваленко
А.А.
Восточноукраинский
национальный университет им. В. Даля
Идентификация динамических объектов в общем
случае состоит в определении их структуры и параметров по наблюдаемым данным -
входному воздействию и выходным величинам.
При этом входное воздействие чаще всего представляет одно из стандартных
возмущений – единичное (ступенчатое), импульсное или гармоническое. Однако во
многих случаях возмущения, действующие на другие каналы объекта, не удается
стабилизировать или хотя бы измерить и их влияние. Это может существенно исказить
результаты эксперимента. Кроме того, на некоторых объектах крайне нежелательным
является подача специальных возмущений.
В этих
случаях для определения динамических характеристик могут быть использованы
статистические характеристики сигналов на входе и выходе объекта, имеющих место
в процессе его нормальной эксплуатации, так называемый пассивный эксперимент.
В этом случае для идентификации объектов производится сбор и анализ информации
о состоянии технологических параметров без специального изменения входных
параметров процесса.
Достоинством
данного метода является то, что практически полностью отсутствуют затраты на
эксперимент. Недостатки - в нормальных условиях эксплуатации колебания
технологического режима невелики и поэтому экспериментальные точки близки друг
к другу. В этих условиях на точность описания могут сильно повлиять случайные
ошибки. Необходимо иметь достаточно большое количество экспериментальных
данных.
Таким
образом, задача разбивается на два
этапа:
1.Определение статистических
характеристик случайных процессов, действующих на объект.
2. Вычисление по ним характеристики
исследуемого объекта.
Статистические характеристики случайного
процесса находятся посредством усреднения значений случайных величин, зависящих
от ординат процесса. Такое усреднение может быть проведено по времени, если
имеется лишь одна реализация процесса, и по множеству для фиксированного
момента времени, когда в распоряжении исследователя имеется множество
независимых реализаций. Случайный процесс, для которого результаты осреднения,
проведенного тем и другим способом, оказываются одинаковыми, обладает
свойством эргодичности [1]. К такому классу относятся
теплогенерирующие объекты, поэтому ниже будем рассматривать стационарные,
эргодические случайные процессы.
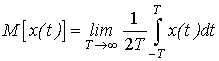 (1)
(1)
Среднее значение
такого процесса постоянно. При вычислении других статистических характеристик
случайного процесса обычно удобно предварительно центрировать его, т. е.
вычесть из ординат процесса его среднее значение.
Вся
необходимая для расчетов линейных систем статистическая информация для
стационарных процессов содержится в их корреляционной
функции, вычисляемой по формуле
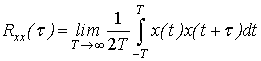 (2)
(2)
При управлении теплогенерирующим
объектом он всегда оказывается охваченным обратной связью, которая может
осуществляться либо через автоматический регулятор [2], либо посредством
человека-оператора, если регулирование производится вручную (рис.1).
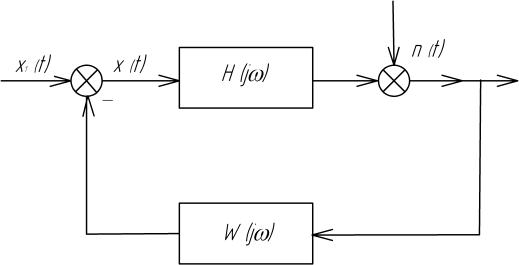
Рис. 1. Структурная схема объекта, охваченного обратной связью
В этом случае входной случайный процесс оказывается коррелированным
через обратную связь с шумом n(t) и уравнением (3) пользоваться нельзя.
Если имеется
такое входное воздействие, которое коррелированно с сигналом на входе регулятора у и не коррелировало с n(t) (на рис. 1 таким воздействием является x1(t)), то импульсную функцию объекта можно найти из
уравнения (3)
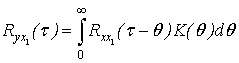 (3)
(3)
методом
преобразования Фурье.
Таким
образом, имея статистические характеристики
входного и выходного сигналов и математическую модель исследуемого объекта, он может быть полностью идентифицирован. При
этом для определения коэффициентов математической модели может быть
использована одна и программ оптимизации [3, 4].
Литература
1.
Булинский А.В. Теория случайных процессов / Булинский А.В., Ширяев
А.Н. -
М.: Машиностроение. - 2005. - 408 с.
2.
Акимов
П.Н. Модели тепломассопереноса в котельных установках /
Акимов П.Н., Андрийчук Н.Д., Гусенцова Я.А. - Луганск: вид.
СНУ
ім.
В. Даля, 2011. – 148 с.
3.
Коваленко А.О. Планування та обробка результатів випробувань
гідропневмосистем/ Коваленко А.О., Сьомін Д.О., Роговий А,С., Пілавов М.В.-
Луганськ: Вид-во СНУ ім.. В Даля, 2011. – 216 с.
4.
Б.
Банди. Методы оптимизации/ Б.Банди. – М.: Радио и связь, 1988. – 128 с.