УДК 519.85
РЕШЕНИЕ ОДНОГО КЛАССА
ЗАДАЧ НАЗНАЧЕНИЯ ГЕОМЕТРИЧЕСКИХ ОБЪЕКТОВ
Е.Ю.Стоян, И.Ю.Тарасов
Харьковский государственный университет питания
и торговли
г. Харьков, ул
Клочковская,333, тел: 330-05 94
Пусть
имеется область размещения ![]() и n геометрических объектов
и n геометрических объектов ![]() ,
, ![]() , с заданными
формами и метрическими характеристиками. Каждому объекту соответствует
внутренняя точка, которую назовем полюсом объекта. Области размещения
принадлежат n точек
, с заданными
формами и метрическими характеристиками. Каждому объекту соответствует
внутренняя точка, которую назовем полюсом объекта. Области размещения
принадлежат n точек ![]() . Требуется таким
образом разместить объекты
. Требуется таким
образом разместить объекты ![]()
![]() , в области
, в области ![]() , совмещая их
полюса с точками
, совмещая их
полюса с точками ![]() , чтобы суммарная
площадь попарных пересечений объектов и площадь той
части объектов, которые не принадлежат
, чтобы суммарная
площадь попарных пересечений объектов и площадь той
части объектов, которые не принадлежат ![]() , была минимальной. В
дальнейшем объект
, была минимальной. В
дальнейшем объект ![]() , установленный на
место
, установленный на
место ![]() , обозначим через
, обозначим через ![]() .
.
Рассмотрим математическую
постановку описанной задачи. Введем булевы переменные:

Для каждого объекта ![]() и каждого места
и каждого места ![]() определим меру
(площадь) части объекта
определим меру
(площадь) части объекта ![]() , не
принадлежащей области
, не
принадлежащей области ![]() :
:
![]() .
.
Кроме того, для объекта ![]() , назначенного на место
, назначенного на место
![]() , и объекта
, и объекта ![]() , назначенного на место
, назначенного на место
![]() , определим меру их
пересечения:
, определим меру их
пересечения:
![]()
![]() .
.
Объекты на места будем назначать
таким образом, чтобы минимизировать следующую функцию:
![]() (1)
(1)
при следующих ограничениях на переменные;
![]() 2J (2)
2J (2)
Смысл этих ограничений
заключается в том, что на каждое место назначается только один объект и каждый
объект может быть установлен только на одно место.
Для простоты дальнейшего
изложения метода решения задачи (1)-(2) осуществим следующие преобразования.
Вместо переменных ![]()
![]() , будем рассматривать
вектор
, будем рассматривать
вектор ![]()
![]() - целая часть числа t . Множество всех таких векторов
обозначим
- целая часть числа t . Множество всех таких векторов
обозначим ![]() . Очевидно, что
все точки множества
. Очевидно, что
все точки множества ![]() и только они
удовлетворяют системе
и только они
удовлетворяют системе

В результате проведенных
преобразований можно сформулировать следующую задачу:
![]() (5)
(5)
![]() (6)
(6)
![]() J (7)
J (7)
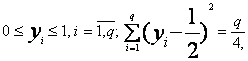 (8)
(8)
где
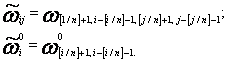 (9)
(9)
Представляет интерес
преобразование целевой функции ![]() к выпуклому
виду, т.е. построение такой выпуклой функции
к выпуклому
виду, т.е. построение такой выпуклой функции ![]() , которая в
точках множества
, которая в
точках множества ![]() совпадает с
совпадает с ![]() . Такое преобразование дня квадратичной функции может быть
проведено на основе следующих справедливых для точек и множества соотношений:
. Такое преобразование дня квадратичной функции может быть
проведено на основе следующих справедливых для точек и множества соотношений:
![]() (10)
(10)
![]() (11)
(11)
Очевидно, что в правых частях
приведенных соотношении - выпуклые
функции. Тогда целевая функция вида (5)
при замене (10)-(11) после преобразований также выпукла. Заметим, что в функции
вида (5)
коэффициенты ![]() , в связи, с чем при
преобразовании к выпуклому виду используется лишь соотношение (10). Однако для преобразования к выпуклому
виду квадратичной функции общего вида необходимы оба соотношения (10) и (11).
, в связи, с чем при
преобразовании к выпуклому виду используется лишь соотношение (10). Однако для преобразования к выпуклому
виду квадратичной функции общего вида необходимы оба соотношения (10) и (11).
Целевая функция (5) может быть записана в следующей форме:
![]() ,
,
где ![]() - симметричная матрица квадратичной
части функции
- симметричная матрица квадратичной
части функции ![]() ;
; ![]() - вектор линейной части функции
- вектор линейной части функции ![]() • Осуществим
преобразование
• Осуществим
преобразование ![]() к выпуклому виду. Имеем
к выпуклому виду. Имеем
![]()
При пересечении гиперплоскостей (6), (7) с n-сферой (9) образуется гиперсфера размерностью S=q-2n-1. Опишем способ проведения вышеупомянутой
редукции размерности задачи. Обозначим

Осуществив ортогонализацию матрицы ![]() , получим матрицу V . Обозначим
, получим матрицу V . Обозначим
![]() .
.
В результате проведенного
преобразования булевы векторы имеют размерность S=q-2n-1, а ограничения
(6)-(7) исключаются.
Перенесем центр сферы S в начало
координат евклидова пространства. Для этого проведем замену переменных задачи.
Обозначим ![]() . В результате последних преобразований математическая
постановка задачи будет иметь следующий вид:
. В результате последних преобразований математическая
постановка задачи будет иметь следующий вид:
![]() (12)
(12)
![]() (13)
(13)
![]() (14)
(14)
где A - положительно определенная симметричная
матрица ![]()
Опишем метод решения задачи (12)-(14). Определим вначале минимум функции F(Z) на сфере s , задаваемой теперь соотношением (14).
Составим функцию Лагранжа задачи (12)-(13):
![]()
Минимум F(z) на сфере может быть найден из следующей
системы:
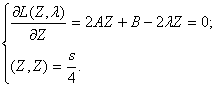
Из первого уравнения системы имеем
![]()
Пусть ![]() - собственные
значения, а
- собственные
значения, а ![]() - соответствующие им
собственные векторы. Тогда если
- соответствующие им
собственные векторы. Тогда если ![]() не принадлежит спектру
матрицы A , то
не принадлежит спектру
матрицы A , то
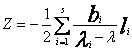 (15)
(15)
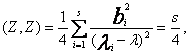 (16)
(16)
где ![]()
Соотношение (16) представляет собой уравнение с одним
неизвестным ![]() . Нетрудно видеть, что на каждом из промежутков
. Нетрудно видеть, что на каждом из промежутков ![]() функция
функция 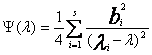 выпукла. Решив уравнение (16) на каждом из промежутков
выпукла. Решив уравнение (16) на каждом из промежутков ![]() одним из
известных численных методов,
получим не более 2S корней
одним из
известных численных методов,
получим не более 2S корней ![]() . При этом
. При этом

Вычислив функцию F(Z) при каждом ![]() , определим минимальное
значение функции и корень
, определим минимальное
значение функции и корень ![]() , при котором
оно достигается. Подставив
, при котором
оно достигается. Подставив ![]() в (13), определим
в (13), определим
![]() . Таким образом, F(Z) достигает
минимума на сфере S в точке
. Таким образом, F(Z) достигает
минимума на сфере S в точке ![]() . Рассмотрим
компоненты вектора
. Рассмотрим
компоненты вектора ![]() . Среди них
выберем те
. Среди них
выберем те ![]() , для которых не
выполняются ограничения -неравенства
задачи (12). (Заметим, что если все
удовлетворяют ограничениям - неравенствам
задачи (12), то
, для которых не
выполняются ограничения -неравенства
задачи (12). (Заметим, что если все
удовлетворяют ограничениям - неравенствам
задачи (12), то ![]() - ее решение). Зафиксировав
переменные, мы тем самым понизим размерность задачи на число зафиксированных
компонент. После преобразования функции цели и ограничений в соответствии с
проведенным понижением размерности задачи мы получаем задачу, аналогичную (12), в пространстве меньшей размерности.
Понижая таким образом на каждом шаге размерность задачи, ми не более чем за. s шагов получим
вектор
- ее решение). Зафиксировав
переменные, мы тем самым понизим размерность задачи на число зафиксированных
компонент. После преобразования функции цели и ограничений в соответствии с
проведенным понижением размерности задачи мы получаем задачу, аналогичную (12), в пространстве меньшей размерности.
Понижая таким образом на каждом шаге размерность задачи, ми не более чем за. s шагов получим
вектор ![]() , дающий
приближенное решение задачи (12).
Осуществив обратное преобразование, найдем
, дающий
приближенное решение задачи (12).
Осуществив обратное преобразование, найдем ![]() где
где ![]() . Таким образом,
. Таким образом, ![]() - приближенное решение
задачи о назначении указанных объектов на зафиксированные места.
- приближенное решение
задачи о назначении указанных объектов на зафиксированные места.
Был
проведен вычислительный эксперимент, в ходе которого при решении различных
задач описанным методом в большинстве случаев было получено оптимальное
решение.