А.П.Мустафаев

Семипалатинский государственный университет имени Шакарима

Об одном методе решения задачи Коши для волнового уравнения

Многие задачи техники и физики позволяет к исследованию дифференциальных уравнений с частными производными второго порядка. Их подробное изучение дает возможность построить теорию широкого круга физических и технических задач.

В основном встречающихся в практике уравнения с частными производным имеют целые семейство решений.

В заданной области изменения переменных и при соответствующих выборе постоянных возможно решить любую задачу Коши для дифференциального уравнения п-го порядка. А для уравнения с частными производными дело обстоит сложнее. Однако и здесь можно ставить вопрос об общем решения зависящейся от произвольных постоянных, значение которых можно определить используя начальные данные.

Рассмотрим волновое уравнение

(1)

с начальным условием

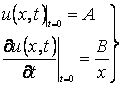(2)

где А и В – заданные действительные числа.

Вводя в место x, t новую переменную зависящая от характеристик

(3)

уравнении (1) приводится к дифференциальному уравнению вида

(4)

Решая полученные уравнения и перехода к старым переменным, получим общее решения уравнения (1) зависящие от произвольных постоянных и , т.е.

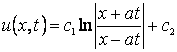(5)

Используя начальные условия получим решение задачи Коши, а именно

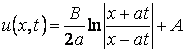(6)

Рассмотрим снова задачу Коши для волнового уравнения (1) при начальных условиях

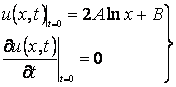(7)

пологая, получим дифференциальное уравнение, общее решение которого имеет вид

Таким образом

Применяя теперь во внимание начальные условия (7) получим решения задачи Коши для уравнения (1)

Нетрудно проверить непосредственным дифференцированием или с использованием формулы Даламбера, что полученные для есть действительно решения волнового уравнения (1) удовлетворяющее соответственно начальным условиям (2) и (7).