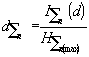S.Sh. Kazhikenova
Karaganda University, Karaganda, Kazakstan
About information estimation of
technological
products quality
Entropy
is a concept, which played a central role in a number of science fields,
namely, in statistical mechanics and theory of information. Using the apparatus
of probability theory permitted in the recent years to clear up the connections
between various usages of entropy. The exact concepts of entropy and mathematics
which appeared at the end of the 40-s and became stable first in the applied
fields, namely, in the communication theory and cybernetics, were immediately
subjected to a thorough mathematical processing and developed in some new
fields of science. Fast, almost momentary introducing these concepts into
different branches of mathematical, technical, social disciplines was
conditioned by the fact that the corresponding mathematical apparatus for their
analysis had already been prepared and, which is principal, there were problems
which were waiting for the concept of entropy in one or another form, and
solved with its help soon. In this
connection on the basis of Shannon information
entropy we have worked out a method of unifying still separate indices for extracting
valuable components and their content in industrial products on processes and
on the whole according to a technological scheme with the following using of
this method for analyzing and comparative estimation of
chemical-and-metallurgical industries. Algorithms of calculating the
information capacity of the system suggested by Shannon permit to clear up the
ratio of the determined information to the quantity of stochastic information
and thus to give the possibility to determine the quality and quantity
estimation of a certain technological scheme. In the general characteristic of
the entropy-and-information analysis of any objects there is used Shannon statistic
formula [1]:
, (1)
where ði is a probability of detecting
a system element;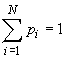 
, 
.
We have
considered this formula use for the quantity estimation of a product or a technical
process quality uncertainty through the uncertainty of the major element of the
system. As a probability of detecting the major element of a technological
system there can be taken its content in the product expressed in a unit
shares. For example, this is the
content of the extracted chemical element in the products of a technological
process. The same is true for the process of extracting an element in one or
another product, because in such a case the extraction index is equal to the
possibility of this element transition from one system state to another. To
estimate the product quality or technological processes both of these two
indices, content and extraction, can be in the equal degree be used.
Theorem 1. Let the own information of
the technological system elements, consisting of N elements, be
equal
. (2)
Then the entropy of the given discrete multitude is
determined by:
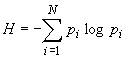, (3)
where ði is a probability of detecting
a system element;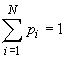 
, 
.
Theorem 2. If a multitude of discrete
probabilistic distributions has N
elements, then the information entropy of the final discrete probabilistic
distribution satisfies the condition:
.
Besides,
then and only then, when the
discrete multitude contains en element of the unit probabilistic element and 
then and only then, when the
discrete multitude has a uniform distribution, i.e. 
, 
Theorem 3. If 
, 
are relative values of the information
, entropy
and on the basis of the law entropy and information sum preservation
there is satisfied the condition:
, (4)
then
is the solution of the equation:
,
where 
The theorems proved show a continuous connection of the determination
and stochastic components, of which the first is the dominating one and ensures
stability, and the other determines the finest changes and the optimal information
capacity of technological systems. The basis of the entropy-and-information
analysis of technological processes is suggested by Shannon method of calculating
the quantity of stochastic and determined information. Suggested by Shannon
method of calculating the quantity of information and entropy turned out to be
so universal, that its use is not limited by the narrow limits of purely
technical applications. Before the publication of Shannon theory, R. Hartley
suggested to determine the quantity of information by the formula which in
relation to the levels has the form [2]:
,
(5)
where n
is a ordinary number of the level considered, 
; k is the length of elements
code at each of the levels of the hierarchy system; 
is the number of technological
system level elements taken the starting point of counting, n=0.
Let’s
consider a technological scheme with 
, i.e. 
in such a case is the selection
from a multitude of elements, an element and not element, containing in the
product. Then (5) will take a form:
.
A
principally important advantage of the information estimation of products quality
or technological operations is that the suggested index
, as any entropy-and-information value, can be summed for reflecting the
whole system in this index. This property of additivity is immanently characteristic
for entropy and information and is the base for expressing the law of their sum
preservation [3]. Consequently, the technological
uncertainty of different operations in the limits of a single technological
scheme can be expressed by the system index of uncertainty:
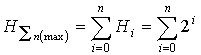bit/el., (6)
From
the formulae for the determination and maximal information it follows that the
determination 
and the system 
ñîmponents of
information are determined by the equalities:
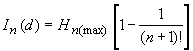bit/el., 
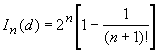bit/el., (7)
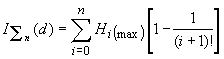bit/el., 
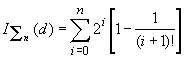bit/el., (8)
The
results of the calculations carried out for 
are presented in Table 1.
We have
established the difference between the system and the level data, namely, that
integral values of determination are less than those differentiated by levele
due to taling into account the information of previous levels, characterized by
larger stochastic properties. We see that when transiting to the higher
structural level there comes into force the law or principle of the progressive
increasing of diversity. As probabilities at these levels don’t effect the
production quality, in calculations it’s possible to take into account only
inter-level correlations. The difference between harmonized, differentiated and
integral models will be illustrated graphically in coordinates 
in accordance to Figure 1.
Òàble 1 – Calculated
entropy-and-information characteristics of technological processes in hierarchical system for 
, 
|
|
bit/el. |
bit/el. |
|
bit/el.
|
|
|
|
0 |
0 |
1,0 |
0 |
0 |
1,0 |
0 |
|
1 |
1,0000 |
2,0 |
0,5000 |
1,0000 |
3,0 |
0,3333 |
|
2 |
3,3333 |
4,0 |
0,8333 |
4,3333 |
7,0 |
0,6190 |
|
3 |
7,6667 |
8,0 |
0,9583 |
12,0000 |
15,0 |
0,8000 |
|
4 |
15,8667 |
16,0 |
0,9917 |
27,8667 |
31,0 |
0,8989 |
|
5 |
31,9556 |
32,0 |
0,9986 |
59,8222 |
63,0 |
0,9496 |
|
6 |
63,9873 |
64,0 |
0,9998 |
123,8095 |
127,0 |
0,9749 |
|
7 |
127,9968 |
128,0 |
1,0 |
251,8063 |
255,0 |
0,9875 |
|
8 |
255,9993 |
256,0 |
1,0 |
507,8056 |
511,0 |
0,9937 |
|
9 |
511,9999 |
512,0 |
1,0 |
1019,8055 |
1023,0 |
0,9969 |
|
10 |
1024,0000 |
1024,0 |
1,0 |
2043,8055 |
2047,0 |
0,9984 |
|
11 |
2048,0000 |
2048,0 |
1,0 |
4091,8055 |
4095,0 |
0,9992 |
|
12 |
4096,0000 |
4096,0 |
1,0 |
8187,8055 |
8191,0 |
0,9996 |
|
13 |
8192,0000 |
8192,0 |
1,0 |
16379,8055 |
16383,0 |
0,9998 |
|
14 |
16384,000 |
16384,0 |
1,0 |
32763,8055 |
32767,0 |
0,9999 |
|
15 |
32768,000 |
32768,0 |
1,0 |
65531,8055 |
65535,0 |
1,0 |
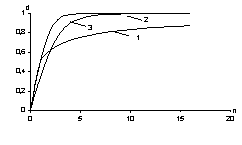
is
level, 
is
determination: 1 – harmonized, 2 – differentiated, 3 – integral
Figure 1 – Dependence of
determination degree on level
It’s obvious
that the harmonized one is nearer to the integral one, for which the value of
determination is less due to the contribution of the lower levels,
characterized by larger stochastic determination. The integral one seems to
depend significantly on the element 
code length. At the second level of an abstract technological scheme
there is obtained a value practically coinciding with the golden section ratio.
From here, in the arbitrary element base there must be especially widely spread
three-level systems with the binary principle of organization.
LIST OF LITERATURE
1. Shannon K.E. Mathematical theory of connection // Works on the
theory of the information and cybernetics. - M.:SILT,1963.With.243-332 ð.
2. Hartley R. Transfer of the information / the Theory of the
information and its appendix. - M.: SILT, 1959. With. 5-35 ð.
3. Ìàlyshev V.P. Probabilistically determined image. -
Almaty: Gylym, 1994. - 376 p.