Мельник В.Н., Карачун В.В.

Национальный технический университет Украины «КПИ»

ОСОБЕННОСТИ ШАРИКОВОЙ КОРРЕКЦИИ

В АКУСТИЧЕСКИХ ПОЛЯХ

В качестве примера рассмотрим одну из технических реализаций гирогоризонта.

Основу конструкции, как всегда, составляет гироскоп 1 с тремя степенями свободы, установленный в кардановом подвесе с вертикальной (в положении равновесия на неподвижном основании) осью собственного вращения ротора (рис. 1). Над кожухом имеется так называемая каретка 4 с прорезью 5, в которой помещен стальной шарик 6, перекатывающийся в кольцеобразном желобе на поверхности кожуха. Каретка приводится во вращение устройством из постоянного магнита 2, насаженного на ось ротора гироскопа, и стаканчика 3, жестко связанного с кареткой. При вращении магнита вместе с ротором, наводимые в стаканчике 3 вихревые токи, взаимодействуя с магнитом, создают момент, направленный в сторону вращения ротора. Скорость вращения каретки регулируется специальным анкерным механизмом.

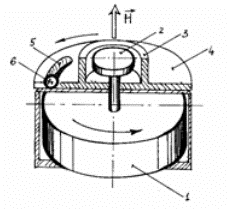
Рис. 1. Гирогоризонт с шариковой коррекцией

Если ось гироскопа в начальный момент времени была вертикальна, то ось фигуры будет описывать конус, так как момент, создаваемый шариком, будет менять свое положение со скоростью, приблизительно равной угловой скорости вращения каретки. При отклонении оси гироскопа от вертикали шарик стремится скатиться вниз по наклонной плоскости и тем самым будет тормозить или ускорять движение каретки.

При звуковом воздействии, например, в виде плоской волны избыточного давления , чувствительный элемент системы коррекции – шарик – получит направленное движение в сторону распространения звука (рис. 2).

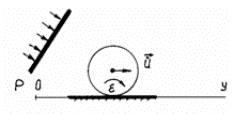
Рис. 2. Схема воздействия акустического излучения на шарик

коррекционного механизма

Определим перемещение шарика под действием акустической волны, считая его абсолютно твердым телом свободным от закреплений и совершающего чистое качение, без проскальзывания. Влиянием стенок желоба на шарик будем пренебрегать.

Пусть в окружающей среде распространяется нестационарная волна давления с потенциалом , фронт которой в момент времени соприкасается с поверхностью исходно неподвижного шарика. В фазовой плоскости функция сохраняет постоянное значение на линиях , поверхность цилиндрическая с образующими, параллельными прямой , направляющая поверхности – кривая при . Потенциал скорости дифракционной волны пусть будет . Тогда, с учетом линейности задачи, дифференциальное уравнение движения шарика можно записать в виде –

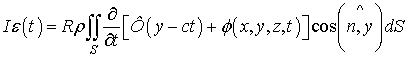, (1)

где – момент инерции шарика относительно точки сопрокосновения с поверхностью качения; – угловое ускорение шарика; – радиус шарика; – плотность воздуха; – потенциал скорости падающей волны давления; – скорость звука; – потенциал скорости дифракционной волны; – направление внешней нормали к поверхности шарика.

Для потенциала справедливо следующее трехмерное волновое уравнение:

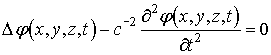, (2)

а начальные условия имеют вид

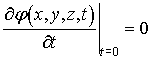; ; . (3)

При 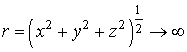функция , а на поверхности тела имеют место граничные условия

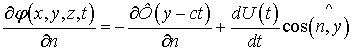. (4)

Определим закон движения шарика. Для этого, проинтегрировав дважды выражение (1) по времени в пределах от до , с учетом обозначенных начальных условий, определим поступательное перемещение шарика

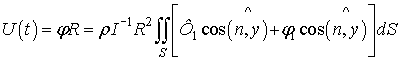, (5)

где ; .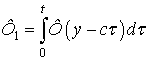

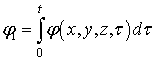Таким образом, перемещения частиц воздуха будут выражаться через функции и формулами

; , (6)

Поскольку падающая волна распространяется вдоль оси , постольку

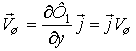. (7)

Для функции справедливо уравнение

(8)

и граничным условиям на поверхности шарика

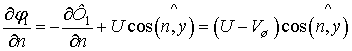. (9)

Выражения (8) и (9) получаются путем интегрирования по времени условий (2) и (4) соответственно с учетом (3).

Следует заметить, что если полный импульс давления конечный по величине, т.е.

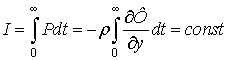, (10)

то сходятся несобственные интегралы и и перемещение останется при конечным по величине, стремясь к некоторому пределу

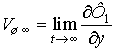. (11)

Поскольку ,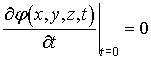

то при установившемся процесс, т.е. при , будет иметь место соотношение

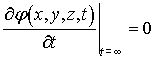
и

,

причем

.

Потенциал скорости падающей волны , а, следовательно, и его интеграл , не имеют особенностей внутри области, занимаемой шариком. На этом основании, в соответствии с формулой Остроградского можно записать

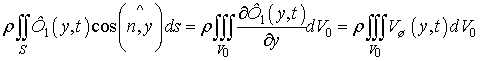, (12)

где справа интегрирование ведется по всему объему, занимаемому шариком.

Тогда

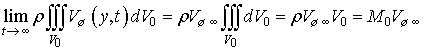, (13)

Что касается второго интеграла выражения (5), то, согласно (9) он может быть записан следующим образом

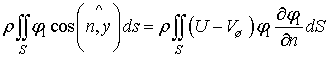. (14)

Для нахождения необходимо определить функцию , которая при принятой общей постановке задачи, разумеется, вычислена быть не может.

Поэтому будем искать не , а только окончательные перемещения

. (15)

Такого предела, вообще говоря, может и не быть. Однако в нашем случае, в предположении конечного по величине импульса давления, частицы воздуха получат конечные перемещения и можно ожидать, что в этом случае конечным будет и перемещение шарика.

Итак, пусть , , а . Тогда из уравнения (15) следует, что

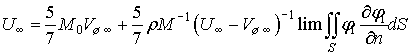. (16)

Таким образом, требуется определить

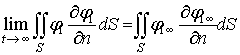, (17)

. (18)

Функция подчиняется уравнению (17), правая часть которого стремится к нулю при , поскольку она пропорциональна давлению в дифракционной волне. Поэтому – функция гармоническая. Она затухает при , а на поверхности шарика подчиняется условию

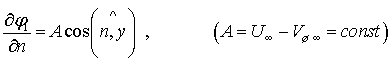. (19)

Отсюда следует, что может быть отождествлена с потенциалом течения безграничной газовой среды при движении в ней рассматриваемого тела с постоянной скоростью в направлении оси . При этом представляет интерес не столько сама эта функция, сколько лишь интеграл (17).

Преобразуем его по формуле Грина с учетом того, что при 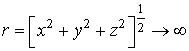функция стремится к нулю как .

Тогда получим

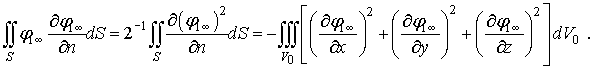(20)

В правой части этого равенства интегрирование распространяется по области задания , т.е. по всему объему воздуха. Таким образом, задача сведена к вычислению интеграла

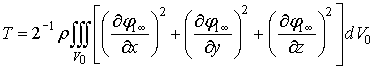. (21)

Но это есть кинетическая энергия идеальной несжимаемой среды в задаче с граничными условиями (19). В первом приближении нашу задачу можно рассматривать именно такой ввиду воздействия акустического излучения высокой интенсивности 160…180 децибел. Тогда следует, что

, (22)

где – коэффициент присоединенной массы для рассматриваемого шарика при его движении вдоль оси .

На основании (20), (21), (22), и (19), выражение (15) примет вид –

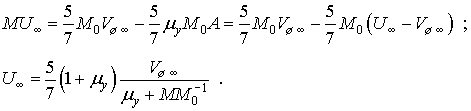(23)

Таким образом, предположение о том, что существует предельное значение перемещения (15), не привело к противоречию и подтверждается окончательной формулой (23). Очевидно, что с прекращением действия акустического излучения, гирогоризонт будет работать в номинальном режиме, предусмотренным паспортными требованиями.