Экономические науки/9.Экономика
промышленности.
Магистрант Турсынбеков
Т., проф., д.э.н.Ертаев
К.
Таразский государственный университет им. М.Х.Дулати, г. Тараз
Оптимизация
распределения инвестиции в экономике
промышленности
В развитии экономики источником развития обычно
выступает прирост инвестиции, а результатом ее использования - прирост
продукции. Чтобы максимально
получить мультипликативный эффект от
развития промышленности за определенный период необходимо оптимально
распределить инвестиции по структурным элементам промышленности. Данная задача имеет нелинейный характер.
Математические модели имеют следующие виды:
модель формирования мультипликативного эффекта
горнодобывающей промышленности:
У1 = -1,97615E-08*Х1^3 + 0,000434256*X1^2 -1,794287742 *X1 +1174,818237, где: У1 - мультипликативный эффект (прирост объема производства)
горнодобывающей промышленности,
млн.тг.;
Х1 - прирост инвестиции в основной капитал
горнодобывающей промышленности, млн.тг.
модель формирования
мультипликативного эффекта обрабатывающей промышленности:
У2 = -1,37791E-08 *Х2^3 + 0,000808929*X2^2 -
10,34311551 *X2 + 3008,12318,
У1 = -1,97615E-08*Х1^3 + 0,000434256*X1^2 -1,794287742 *X1 +1174,818237, где: У2 - мультипликативный
эффект (прирост объема производства)
обрабатывающей промышленности, млн.тг.;
Х2 -
прирост инвестиции в основной капитал обрабатывающей промышленности,
млн.тг.
уравнение тренда
прироста инвестиций в основной капитал промышленности
У3 = 0,242384797 *t^3 + 4525,047294*t^2-17582,62648 *t +18571,46429 ,
где: У3 - прирост инвестиции в основной
капитал промышленности;
t- фактор времени, годы.
На основе данных
уравнений составляем систему уравнений
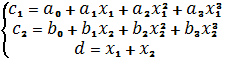
Решить задачу нелинейного программирования - это
значит найти такие значения управляющих переменных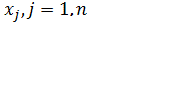 
, которые удовлетворяют
системе ограничений и доставляют максимум или минимум функции
Для решения задач
нелинейного программирования существуют различные методы их решения. К ним
можно отнести: методы множителей Лагранжа,
квадратичное и выпуклое программирование, градиентные методы, ряд приближенных
методов решения, графический метод.
Для решения
данной задачи используем метод множителей Лагранжа. Функция Лагранжа имеет вид
Найдем частные производные функции по 
и 
и приравняем их к
нулю. Получили следующую систему уравнений:
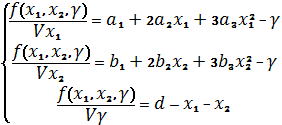
Решая систему, найдем: x1; x2; 
значение
мультипликативного эффекта в экономике промышленности Жамбылской области.
(см.табл.1 )
Значение
определителя, составленного из вторых частных производных функций по
х1,х2, (см.табл.2 ) рассчитывается по следующей формуле:
(а2
+3*а3*х1)*(в2 +3*в3*х2)
Если оно имеет положительное значение, то
считается, что функция действительно имеет экстремум.
По теореме о достаточном условии существования
условного экстремума функция в точке
Х1, действительно имеет экстремум. Если значение уравнения а2 + 3*а3*х1
имеет отрицательное значение, то в
этой точке х1 функция имеет условный максимум. И наоборот. Если оно имеет
положительное значение, то функция в точке х1 - условный минимум. (см.табл.2 )
Прогнозные значения инвестиции в основной капитал промышленности определялись по трендовому методу, а
распределение инвестиции по структурным
элементам промышленностями проводилось
по функции Лагранжа. В результате чего оптимально распределялись инвестиции в
основной капитал среди горнодобывающей и обрабатывающей промышленностей, что
эффекты на прогнозируемый период имеют тенденции к росту. (см.табл.3)
Так, например, для получения максимального
мультипликативного эффекта в экономике промышленности Жамбылской области в
2014г необходимо прирост инвестиций в сумме 17828,46 млн.тг. распределить в сумме 20,68748 млн.тг. в
горнодобывающую промышленность, а в сумме 17807,78 млн.тг. в обрабатывающую промышленность. При этом
мультипликативный эффект от рационального распределения инвестиции на развитие
экономики промышленности Жамбылской области составляет 8670,434 млн.тг. По данным таблиц 3
можно не только определить прогнозные значения экономики
промышленности, но и регулировать их на
основе разработки и реализации экономической политики в рамках Жамбылской области.
Преимуществами в описании формировании
мультипликативного эффекта обладают динамические модели, позволяющие не только
определять основные показатели развития экономики промышленности , но и
получать представление о том, за счет
каких факторов и как будет формироваться траектория экономического развития.
Разработанный нами подход к анализу и прогнозирования формирования мультипликативных эффектов может применяться для
экспертных оценок при обсуждении налоговой и тарифной политики, а также при
определении значимости конкретных крупных инвестиционных проектов. Оценки
возможного мультипликативного эффекта от реализации инвестиционного проекта
могут оказаться полезными для представителей бизнеса и государства при
определении возможных объемах административной или финансовой поддержки со
стороны государства
Литература:
1.Дрейпер Н., Смит Г. Прикладной регрессионный
анализ. Множественная регрессия = Applied Regression Analysis. — 3-е изд. — М.:
«Диалектика», 2007. — С. 912. — ISBN 0-471-17082-8
2.Фёрстер Э., Рёнц Б. Методы корреляционного и
регрессионного анализа = Methoden der Korrelation - und Regressiolynsanalyse. —
М.: Финансы и статистика, 1981. — 302 с.
3. Радченко
Станислав Григорьевич, Методология регрессионного анализа: Монография. — К.:
«Корнийчук», 2011. — С. 376. — ISBN 978-966-7599-72-0