Математика/5. Математическое
моделирование
Искакова Альмира
Мухтаровна
Национальный
центр тестирования
Анализ характеристик
тестовых заданий на основе математической модели Раша (на материале по физике)
В данной статье приведены результаты ВОУД-2015.
На основе данных, полученных в ходе тестирования, анализируются характеристики
тестовых заданий. В соответствии с моделью Раша проведен анализ статистик
согласия по отдельным заданиям теста.
Ключевые слова: модель Раша,
корреляция, дифференцирующая способность, трудность заданий.
В связи с внесениями изменений в закон РК «Об образовании» мониторинговым
исследованием национального уровня c 2012 года является Внешняя оценка учебных достижений
(далее - ВОУД). Важным
составляющим всех экзаменов и мониторингов, проводимых на национальном уровне,
является инструментарий измерения. Любое измерение, особенно педагогическое,
должно иметь математически обоснованные доказательства того, что используемая
методика тестирования является корректной. Слово «измерение» часто используется
не по существу, без должного смыслового содержания. В нашем случае средством
измерения служит тщательно продуманный и специально сконструированный тест, представляющий
собой репрезентативную конечную выборку тестовых заданий, полноправно
характеризующих область знаний.
Традиционно в математическом моделировании
множество экспериментальных данных рассматривается как заданное и ставится
задача поиска модели, которая наилучшим образом с ними согласуется. Однако при
использовании математических моделей в такой сложной области, как
педагогическое тестирование, модель не может быть произвольной.
Модели обладают определенными свойствами,
выполнение которых считается принципиальным. Число параметров, входящих в
модель, должно быть минимально. Математические модели Раша могут быть применены
к заданиям всех форм, которые наиболее часто встречаются в педагогическом
тестировании. Таким образом, в рамках данного подхода модель не является
случайной, она первична по отношению к данным. В условиях модели Раша первичный
балл испытуемого является достаточной статистикой для оценки уровня
подготовленности [1].
Для исследования согласия экспериментальных
данных с моделью измерения в рамках модели Раша существуют различные методы. В
рамках статистической теории главные методы обоснования качества педагогических
измерений – статистические расчеты коэффициентов корреляции, множественный
регрессионный и факторный анализ. Расчет вероятностей правильного ответа
испытуемых разного уровня подготовленности на задания различного уровня
трудности можно назвать ключевым методом модели математической теории
педагогических измерений.
Если какое-нибудь задание не находится в
достаточном хорошем согласии с моделью измерения, это означает, что имеется
искажение в измерении задания.
Рассмотрим анализ заданий теста на предмет
согласия с моделью измерения на примере теста по физике. Всего тест содержит 20
заданий, из них 6 заданий на определение функциональной грамотности. Общее
число испытуемых составило 203 ученика. В результате обработки данных
компьютерными программами RUMM и WINSTEPS были получены основные характеристики
тестовых заданий и графики всех 20 заданий.
Среди многих характеристик, получаемых в
результате анализа заданий, наиболее важными являются три - дифференцирующая
способность, трудность задания и корреляция:
Ø
трудность
заданий – это характеристика теста, отражающая уровень ее решаемости
участниками тестирования. Обычно трудность оценивается при сравнении числа
испытуемых, правильно выполнивших задание, к общему числу испытуемых;
Ø
дифференцирующая
способность тестового задания позволяет выявлять сильных и слабых учащихся,
дифференцировать испытуемых по уровню подготовленности;
Ø
корреляция
представляет собой меру зависимости переменных между баллами по заданию и общим
баллом по тесту.
В таблице 1 приведены статистические данные по
заданиям рассматриваемого варианта теста. Задания в таблице расположены в
порядке их следования в тесте. В 1-й колонке представлен номер задания, во 2-ой
– представлена оценка трудности. Согласно таблице 1, в данном тесте 4 задание
является самым легким, его трудность составляет-0,45 логит. Задания 5 и 16
являются самими трудными, их значения равны 1,34.
Следующая колонка содержит коэффициент
корреляции баллов по заданию с общим баллом по тесту. Далее следуют значения
статистик согласия.
Из данных в таблице 1 следует, что большинство
заданий теста (16 из 20, т.е. 80%) демонстрируют хорошее согласие с моделью:
средние значения общей (OUTFIT MNSQ) и взвешенной общей статистики согласия
(INFIT MNSQ) находятся в пределах (0,5; 1,5) [1]. Средние значения стандартизированной общей (OUTFIT ZSTD) и
стандартизированной взвешенной общей статистики (INFIT ZSTD) находятся в
пределах [-2; 2].
Рассмотрим более подробно задания (7,15,19 и
20), которые имеют значения статистик согласия больше правых критических, а
также показатель коэффициента корреляции менее 0,2.
Таблица
1. - Статистические данные по заданиям теста
|
Номер
задания |
Логит
трудности задания |
Коэффициент
корреляции |
Дифференцирующая
способность |
Статистики согласия |
|||
|
Взвешенные статистики согласия (INFIT) |
Общие статистики согласия (OUTFIT) |
||||||
|
MNSQ |
ZSTD |
MNSQ |
ZSTD |
||||
|
1. |
-0,27 |
0,39 |
0,44 |
1,02 |
0,3 |
1,01 |
0,1 |
|
2. |
1,09 |
0,40 |
0,35 |
1,01 |
0,1 |
0,91 |
-0,6 |
|
3. |
0,69 |
0,43 |
0,49 |
0,99 |
-0,1 |
0,98 |
-0,2 |
|
4. |
-0,45 |
0,37 |
0,46 |
0,98 |
-0,4 |
1,10 |
1,0 |
|
5. |
1,34 |
0,37 |
0,31 |
1,02 |
0,3 |
1,01 |
0,1 |
|
6. |
0,43 |
0,47 |
0,51 |
0,96 |
-0,7 |
0,97 |
-0,3 |
|
7.
|
0,49 |
0,65 |
0,71 |
0,76 |
-3,8 |
0,70 |
-3,6 |
|
8. |
0,41 |
0,54 |
0,55 |
0,88 |
-2,0 |
0,84 |
-1,8 |
|
9. |
0,41 |
0,49 |
0,51 |
0,93 |
-1,2 |
0,90 |
-1,2 |
|
10. |
0,97 |
0,50 |
0,44 |
0,91 |
-1,1 |
0,90 |
-0,7 |
|
11. |
0,49 |
0,52 |
0,54 |
0,90 |
-1,6 |
0,85 |
-1,7 |
|
12. |
0,82 |
0,39 |
0,31 |
1,02 |
0,3 |
1,07 |
0,6 |
|
13. |
0,73 |
0,34 |
0,38 |
1,08 |
1,1 |
1,13 |
1,2 |
|
14. |
0,71 |
0,42 |
0,44 |
1,00 |
0,1 |
0,99 |
0,0 |
|
15. |
0,87 |
0,20 |
0,24 |
1,21 |
2,5 |
1,30 |
2,3 |
|
16. |
1,34 |
0,33 |
0,25 |
1,03 |
0,4 |
1,17 |
1,0 |
|
17. |
0,89 |
0,53 |
0,50 |
0,88 |
-1,5 |
0,81 |
-1,6 |
|
18. |
1,07 |
0,32 |
0,27 |
1,08 |
0,9 |
1,18 |
1,3 |
|
19. |
0,58 |
0,27 |
0,23 |
1,15 |
2,1 |
1,17 |
1,7 |
|
20. |
1,28 |
0,19 |
0,15 |
1,20 |
1,8 |
1,35 |
2,0 |
По полученным характеристическим кривым можно
судить о соответствии экспериментальных данных модели Раша[2]. Разобьем всю
выборку испытуемых на три приблизительно равные группы в соответствии с их
уровнями подготовленности. В первую группу отберем испытуемых с высоким
уровнем, во вторую – со средним и в 3-ю – с низким уровнем подготовленности. На
рисунках эти группы будут отмечены точками. Если задание находится в хорошем
согласии с моделью, то эти три точки будут находиться в достаточной близости от
модельной характеристической кривой задания. В данном случае из приведенных
графиков видно, что самыми проблемными являются 15, 19 и 20 задания, так как
все точки расположены достаточно далеко от модельной кривой. Эти задания вводят
в заблуждение сильных учащихся, которые в результате выполняют его неправильно.
Задания плохо дифференцируют испытуемых и не способны объективно оценить
вероятность правильного ответа у хорошо подготовленных испытуемых. Для них эти
задания оказались труднее, чем прогнозирует модель. На рисунках 1,2 и 3 можно
увидеть характеристические кривые вышеописанных заданий. Графики указывают на
то, что эти задания имеют плохое согласие с моделью. Причины такого дефекта
могут скрываться в словесной формулировке заданий, которые могли быть
непонятными или неправдоподобными именно для этих испытуемых. Точный диагноз
дефекта заданий может дать только экспертиза их содержания, а также форм этих
заданий. Заметим, что корреляция баллов 15 и 20 заданий с общим баллом по тесту
самая низкая и составляет 0,20 и 0,19 соответственно.
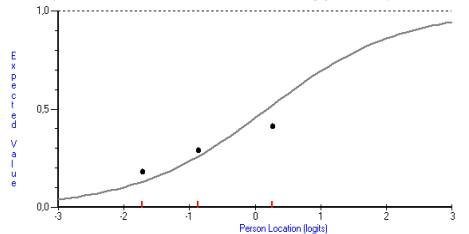
Рисунок 1. Характеристическая кривая
задания №15
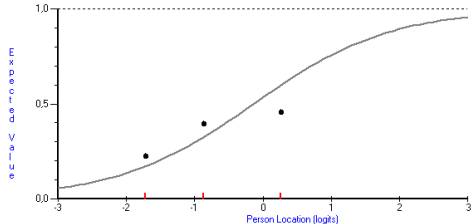
Рисунок 2. Характеристическая кривая
задания №19
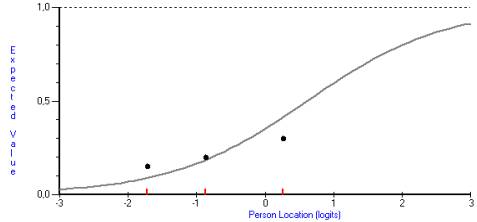
Рисунок 3. Характеристическая кривая
задания №20
7 задание в данном тесте является проблемным в
меньшей степени (Рисунок 4). С точки зрения классической теории педагогических
измерений, это задание обладает относительно высокой дифференцирующей
способностью. Об этом свидетельствует значение коэффициента корреляции ответов
испытуемых на это задание с суммой баллов по всему проектируемому тесту (0.65,
таблица 1). Слабо подготовленные испытуемые отвечают на это задание хуже, чем
это прогнозируется моделью Г.Раша, а хорошо подготовленные испытуемые отвечают
лучше. В результате эмпирическая характеристическая кривая этого задания
отличается от теоретической кривой: наклон эмпирической кривой в точке перегиба
несколько больше, чем у других заданий. Такое отклонение кривых может
объясняться тем, что в тестировании принимало участие недостаточное количество
учащихся. Как советуют специалисты, минимальная выборка должна включать как
минимум 300-400 человек [3,64].В целом такое задание не считается плохим, так
как позволяет дифференцировать учащихся по уровню подготовленности.
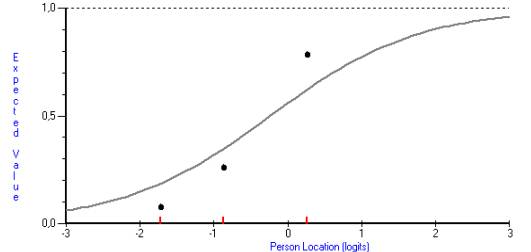
Рисунок 4. Характеристическая кривая
задания №7
Таким образом, проведенное исследование
показало уникальность модели Раша, потому что её применение позволяет
определить задания, несоответствующие модели. Однако следует учитывать, что при
использовании лишь характеристических кривых заданий существует риск удаления
качественных заданий. Следовательно, анализируя задания теста необходимо
учитывать все характеристики тестовых заданий: дифференцирующую способность,
трудность, корреляцию и статистики согласия. Кроме того, исследование показало,
что используемые тестовые задания в ВОУД отвечают требованиям достоверности и
правдоподобности оценки знаний обучающихся, в частности, по физике.
Список использованной литературы
1
Карданова Е.Ю. Моделирование и параметризация тестов: основы теории и
приложения, М,2008.- 76 с.
2
Аванесов В.С. Метрическая система Георга Раша – Rash Measurement,
статья вторая, ж. Педагогические измерения, М, 3/2011г.- 25 с.
3 Пермяков О.Е. Максимова О.А. Основы
технологии
комплексной
экспертизы качества педагогических тестов, Т, 2008 г-64с.
4
Аванесов В.С. «Метрическая система Георга Раша – RashMeasurement», статья первая, ж.
Педагогические измерения, М, 2/2010г.- 75
5 Rasch G. Probabilistic Models for
Some Intelligence and Attainment Test. – Chicago. Mesa Press,1980,199
p
6
Балыкбаев Т.О. Примбетова Г.С. Система внешней оценки качества образования как
элемент Национальной системы оценки качества образования, Педагогические измерения,
М, 1/2011г. - 19 с.