wyznaczniki macierzy – powtórka z rozrywki

matrix determinants

Katarzyna Brożek

Streszczenie

Algebra liniowa należy do działu algebry zajmującej się badaniem przestrzeni oraz przekształceń liniowych. W skład jej zakresu należy zaliczyć między innymi teorie macierzy oraz wyznaczników. Tym ostatnim został właśnie poświęcony niniejszy artykuł. Generalnym celem opracowania jest analiza wyznaczników macierzy, a więc dotyczy to bezpośrednio pewnego wycinka algebry liniowej. Tak też rozważania traktują przede wszystkim o sposobach wyliczania wyznaczników ze względu na stopień macierzy oraz o własnościach wyznaczników. W związku z tym praca stanowi swoistego rodzaju przypomnienie oraz usystematyzowanie wiedzy z prezentowanego zakresu. Artykuł głównie kierowany jest do studentów kierunków ekonomicznych oraz wszystkich osób zgłębiających zaproponowaną tematykę.

Słowa kluczowe: algebra liniowa, własności wyznaczników, wyznaczniki

Abstract

Linear algebra is a branch of algebra that deals with space and linear transformations and incorporates the theories of matrix and determinants. The aim of the present paper is to enunciate the analysis of matrix determinants, ergo it directly pertains to a section of linear algebra. Therefore the discussion primarily concerns the way to calculate determinants taking into account matrix order and determinant properties. The article helps to revise and systematize the knowledge of the subject and is intended for students of economics and anyone exploring the subject area.

Keywords: determinants, determinant properties, linear algebra

1 Wyznaczniki

W teorii macierzy jednym z najistotniejszych pojęć jest wyznacznik macierzy. Bowiem jest ono przydatne m.in. w rozwiązywaniu układów równań liniowych jak i również w przypadku sprawdzania, czy dana kwadratowa macierz jest nieosobliwa. (A. C. Chiang, 1994, s. 103)

Jedna z najbardziej popularnych definicji tego terminu mówi, iż wyznacznikiem macierzy kwadratowej A =[a_ij] stopnia n jest liczba rzeczywista, określona jednoznacznie za pomocą elementów tej macierzy i oznaczona symbolem det A. Warto dodać, iż zamiast det A można używać inne oznaczenia wyznacznika np.: │A│. Wyznacznik z definicji jest skalarem, natomiast macierz nie ma wartości numerycznej. Można wobec tego wysnuć wniosek, iż wyznacznik sprowadza się do liczby, zaś macierz jest całym blokiem liczb. Ponadto wyznaczniki są zdefiniowane tylko i wyłącznie dla macierzy kwadratowych podczas gdy dowolna macierz nie musi być kwadratową.

2. METODY OBLICZANIA WYZNACZNIKÓW

Przy omawianiu wyznaczników bardzo istotny jest również stopień macierzy. Otóż jeżeli macierz A € M (n, n), to liczbę n nazywa się stopniem wyznacznika tej macierzy. (Nykowski, 2005, s. 166). W pierwszej kolejności omówiono reguły obliczania wyznacznika dla macierzy stopnia mniejszego niż 4.

2.1 Obliczanie wyznacznika macierzy stopnia pierwszego

Jeżeli A _{1 ×1} = [a₁₁], to det A = a_11;

np. dla macierzy A= , det A = ││= -3 (zgodnie z definicją, iż wyznacznik macierzy A jest równy elementowi tej macierzy) (Słownik Encyklopedyczny, 2000, s. 317).

2.2 Obliczanie wyznacznika macierzy drugiego stopnia

Jeżeli A _2×2 =, to det A= a₁₁a₂₂-a₁₂a₂₁ (Skwarczyński, 1987, s. 170)

np. det= 12-35=-23

otrzymany został poprzez wymnożenie dwóch elementów głównej przekątnej macierzy A oraz odejmując iloczyn dwu pozostałych elementów. Podobny schemat zwany schematem Sarrusa, można wykorzystać do obliczania wyznacznika stopnia trzeciego, ale tylko trzeciego!

2.3 Obliczanie wyznacznika macierzy trzeciego stopnia

Jeżeli A _3×3 =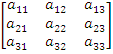

należy zapisać wyznacznik jako kombinację liniową wyznaczników 2×2, uzyskując:

│A│=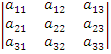=(-1)¹⁺¹*a₁₁+(-1)¹⁺²*a₁₂*+(-1)¹⁺³* a₁₃

Następnie wykorzystując wzór na wyznacznik macierzy 2×2, otrzymano:

│A│ = a₁₁(a₂₂a₃₃-a₂₃a₃₂)-a₁₂(a₂₁a₃₃-a₂₃a₃₁)+a₁₃(a₂₁a₃₂-a₂₂a₃₁)

Po przekształceniu:

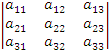=a₁₁a₂₂a₃₃+a₁₂a₂₃a₃₁+a₁₃a₂₁a₃₂-a₁₁a₂₃a₃₂-a₁₂a₂₁a₃₃-a₁₃a₂₂a₃₁
(Leitner,1994, s. 84-85).

Praktyczna metoda wykorzystywania uzyskanej zależności zwana jest wcześniej już wspomnianą metodą Sarrusa. Bowiem polega ona dopisaniu do wyznacznika dwóch pierwszych kolumn/wierszy i obliczeniu odpowiednich iloczynów zgodnie z następującą zasadą. Mianowicie, należy dodać iloczyny utworzone z wyrazów leżących na przekątnej głównej oraz przekątnych równoległych (o kierunku prawym) oraz odjąć iloczyny tworzone z wyrazów leżących na przekątnych o kierunku lewym. (Gurgul, Suder, 2012, s. 150).

+ + +

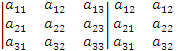= a₁₁a₂₂a₃₃+a₁₂a₂₃a₃₁+a₁₃a₂₁a₃₂-a₁₁a₂₃a₃₂-a₁₂a₂₁a₃₃-a₁₃a₂₂a₃₁

– – –

np. C=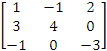

det C = =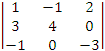

= 1*4*(-3)+(-1)*0*(-1)+2*3*0-2*4*(-1)-1*0*0-(-1)*3*(-3)=-13

Aby zastosować schemat Sarrusa należy:

1. Dopisać dwie początkowe kolumny macierzy z jej prawej strony;

2. Utworzyć zgodnie z przebiegiem linii ukośnych trzech iloczynów „dolnych” ze znakiem plus i trzech iloczynów „górnych” ze znakiem minus;

3. Wyznaczyć sumy wszystkich sześciu iloczynów.

2.4 Obliczanie wyznaczników macierzy wyższych stopni

Pierre Simon Laplace[1] przyczynił się do wprowadzenia praktycznej metody obliczania wyznaczników poprzez opracowanie tzw. rozwinięcia Laplace’a. Wyznacznik macierzy kwadratowej można obliczyć stosując rozwinięcie względem dowolnego wiersza lub dowolnej kolumny. Skoro nie ma znaczenia względem, którego wiersza bądź której kolumny należy rozwijać dany wyznacznik to najlepiej jest wybrać taki wiersz, kolumnę, który zawiera najwięcej zer (ponieważ element a_ij = 0 to wówczas nie ma konieczności jego dopełnienia, gdyż ich iloczyn wynosi a_ij x A_ji = 0). W tym celu należy obliczyć dopełnienie algebraiczne elementu a_ij macierzy kwadratowej A (Gleichgewicht, 2004, s. 117-120). Tę liczbę definiuje się w następujący sposób:

= (-1)^i+jdetA_ij

gdzie Aij oznacza macierz powstałą z macierzy A przez wykreślenie z niej i-tego wiersza oraz j-tej kolumny.

W tym miejscu konieczna jest znajomość podstawowych pojęć związanych z macierzami.

Rzędem r (W) macierzy W nazywa się największy stopień wyjętego z niej różnego od zera minora, przy czym jeżeli wszystkie elementy macierzy są równe zero, to przyjąć należy, że rząd jej jest równy zero (Krysicki, Włodarski, 2014).

Własności rzędu macierzy są zbliżone do własności wyznaczników, co jest zrozumiałe z uwagi na definicję rzędu. Do własności tych należy zaliczyć: (Hohenberg, 1974, s.66)

1. Rząd macierzy nie zmienia się na skutek przestawienia dwóch wierszy/kolumn macierzy.

2. Transpozycja wierszy macierzy na kolumny (i odwrotnie) nie zmienia rzędu macierzy.

3. Rząd macierzy nie zmieni się, jeżeli usuniemy z macierzy wiersz/kolumnę złożony z samych zer.

4. Rząd macierzy nie zmieni się, jeżeli usuniemy z macierzy wiersz/kolumnę, który jest kombinacją liniową innych wierszy/kolumn.

5. Rząd macierzy nie zmieni się, jeżeli pomnożymy dowolny wiersz/kolumnę macierzy przez dowolną liczbę k ≠ 0.

6. Rząd macierzy nie zmieni się, jeżeli do dowolnego wiersza/kolumny macierzy dodamy dowolną kombinację liniową innych wierszy/kolumn.

Minorem n-tego stopnia w macierzy A nazywamy wyznacznik macierzy kwadratowej wymiaru n x n powstałej z A po wykreśleniu z niej pewnej liczby wierszy i kolumn. Jeżeli macierz A jest kwadratowa i wykreślimy z niej i-ty wiersz oraz j-tą kolumnę to taki minor jest oznaczony symbolem M_ij.

Dla macierzy A = istnieją trzy minory stopnia drugiego (z tej macierzy nie ma możliwości uzyskania minorów stopnia wyższego). Pierwszy powstanie przez skreślenie pierwszej kolumny:

→|A₂| = = 4

Drugi uzyska się poprzez skreślenie drugiej kolumny:

→|A’₂| = = -5

Trzeci minor drugiego stopnia powstanie poprzez skreślenie trzeciej kolumny:

→|A’’₂| = = -2

Z macierzy A można uzyskać aż 6 minorów pierwszego stopnia. Jednym z nich jest wyznacznik macierzy powstałej przez skreślenie pierwszego wiersza oraz pierwszej i drugiej kolumny, tj:

→|A₁| = = 2

Obliczanie wyznacznika macierzy czwartego stopnia. Można to uzyskać na dwa sposoby, mianowicie:

a) rozwijając go względem wybranego wiersza;

b) względem wybranej kolumny.

C =

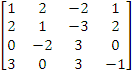
Ad. a. Na początku należy zwrócić uwagę w którym wierszu znajduje się najwięcej zer. W wierszu trzecim występują aż dwa zera wobec tego szukany wyznacznik będzie rozwinięty względem trzeciego wiersza.

Skoro c₃₁ = c₃₄ = 0 to:

det C = (-2) * (-1)³⁺² * 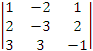+ 3 * (-1)³⁺³ *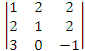

Na tym etapie wystarczy metodą Sarrusa obliczyć dwa wyznaczniki stopnia 3, tj.:

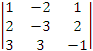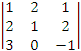= -4 oraz = 12

A zatem detC = 2 * (-4) + 3 *12 = 28

Ad. b. Wyznacznik |C| można również rozwinąć względem pierwszej, drugiej lub czwartej kolumny ponieważ w każdej z nich występuje jedno 0. Do obliczeń wybrano kolumnę drugą. c₄₂ = 0

detC = 2 * (-1)¹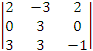⁺² * +1 * (-1)²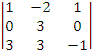⁺² * + (-2) * (-1)³⁺²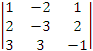

Należy następnie obliczyć wyznaczniki występujące w powyższym wyrażeniu:

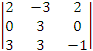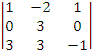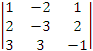= -24, = -12 oraz = -4

3. Własności wyznaczników

Wyznacznik posiadają osiem podstawowych własności, do nich należą:

1. Wyznacznik macierzy kwadratowej, która posiada kolumnę-wiersz złożoną z samach zer jest równy 0.

det 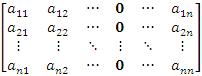= 0

2. Wyznacznik macierzy kwadratowej zmieni znak, jeżeli przestawimy między sobą dwie (dwa) kolumny (wiersze).

det 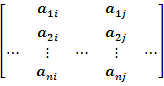= -det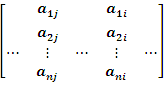

3. Wyznacznik macierzy kwadratowej mającej dwie (dwa) jednakowe kolumny (wiersze) jest równy 0.

det 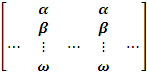= 0

4. Jeżeli wszystkie elementy pewnej kolumny (pewnego wiersza) macierzy kwadratowej zawierają wspólny czynnik, to czynnik ten można wyłączyć przed wyznacznik tej macierzy.

det 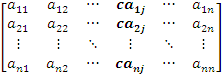= c det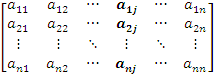

ponadto

det 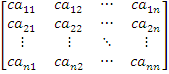= cⁿ det

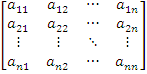
5. Wyznacznik macierzy kwadratowej, której elementy pewnej kolumny (pewnego wiersza) są sumami dwóch składników jest równy sumie wyznaczników macierzy, w których elementy tej kolumny (tego wiersza) są zastąpione tymi składnikami.

det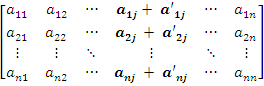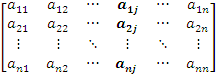

= det + det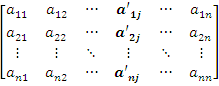

6. Wyznacznik macierzy nie zmieni się, jeżeli do elementów dowolnej kolumny (wiersza) dodamy odpowiadające im elementy innej kolumny (innego wiersza) tej macierzy pomnożone przez dowolną liczbę.

Ogólnie: wyznacznik macierzy nie zmieni się, jeżeli do elementów dowolnego wiersza (kolumny) dodamy sumę odpowiadających im elementów innych wierszy (kolumn) tej macierzy pomnożonych przez dowolne liczby.

det

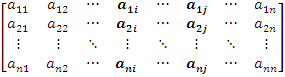
= det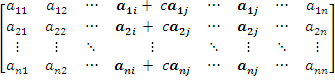

7. Wyznacznik macierzy kwadratowej i jej transpozycji są równe.

det =

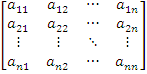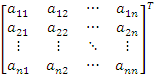
8. Niech A₁, A₂,…, A_k będą macierzami kwadratowymi, niekoniecznie tych samych stopni. Wtedy

det 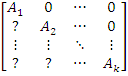= det A₁ * det A₂ *…* det A_k

gdzie symbole 0 oznaczają macierze zerowe, a symbole ? dowolne macierze odpowiednich wymiarów (Lassak, 2010, s. 12).

Podsumowanie

Algebra ma bardzo szerokie zastosowanie w teorii liczb, analizie funkcjonalnej, teorii równań różniczkowych, geometrii, programowaniu liniowym ale i również w innych dyscyplinach matematyki. Natomiast algebrę liniową wykorzystuje się do badania grup pierścieni itp. Przez podanie ich reprezentacji w przestrzeniach liniowych – reprezentacja liniowa.

Macierze stosuje się w celu szybkiego rozwiązywania skomplikowanych układów równań liniowych tzn. w takich, w których jest wiele niewiadomych i występuje wiele równań. Za pomocą macierzy można osiągnąć:

· zapis każdego układu równań;

· wyznacznik macierzy służy do znajdowania macierzy odwrotnej oraz rozwiązywania układów równań za pomocą wzorów Cramera;

· rząd macierzy pozwala określić ile rozwiązań ma układ równań liniowych (Poradnik inżyniera. Matematyka, 1986, s. 102).

Bibliografia

1. CHIANG, A. C. Podstawy ekonomii matematycznej, Warszawa: Polskie Wydawnictwo Ekonomiczne, 1994. s.103. ISBN 83-208-0942-8.

2. GLEICHGEWICHT, B. Algebra, wydanie drugie, Wrocław: Oficyna Wydawnicza GiS, 2004. s.117-120. ISBN 83-89020-35-1.

3. GURGUL, H., SUDER, M. Matematyka dla kierunków ekonomicznych, wyd. IV, Warszawa: Oficyna a Wolters Kluwer Business, 2012. s. 136, 150. ISBN 978-83-264-4700-6.

4. HOHENBERG, R. Matematyka dla ekonomistów. Podręcznik. Warszawa: Państwowe Wydawnictwo Naukowe, 1974, s. 66

5. KRYSICKI, W., WŁODARSKI, L. Analiza matematyczna w zadaniach, część I. Warszawa: Wydawnictwo Naukowe PWN, 2014. ISBN 978-83-01-14295-7.

6. LASSAK, M. Matematyka dla kierunków ekonomia, zarządzanie, marketing, bankowość, Warszawa: Wydawnictwo WM Sp. z o. o, 2010. s. 12. ISBN 83-86194-32-4.

7. LEITNER R. Zarys matematyki wyższej dla studentów, cz. 1, wydanie 13, Wydawnictwo Naukowo-Techniczne, 1994. s. 84-85, ISBN 83-204-3067-4.

8. NYKOWSKI, I. red. Matematyka, Warszawa: Szkoła Główna Handlowa w Warszawie – Oficyna Wydawnicza, 2015. s.137. ISBN 83-7378-068-8.

9. PORADNIK INŻYNIERA. MATEMATYKA. Wydanie 2 zmienione, tom 1, Warszawa: Wydawnictwa Naukowo Techniczne, 1986, s.102. ISBN, 83-204-0675-7.

10. SKWARCZYŃSKI, M. Wykłady z matematyki. Algebra liniowa, cz. 1, Skrypty Uczelniane, Radom: Wyższa Szkoła Inżynierska im. K. Pułaskiego w Radomiu, 1987. s.170. ISSN 0239-6459.

11. SŁOWNIK ENCYKLOPEDYCZNY. MATEMATYKA. Wrocław: Wydawnictwo Europa, 2000. s.317. ISBN 83-85336-06-0.

Kontakt

mgr Katarzyna Brożek

Uniwersytet Technologiczno-Humanistyczny im. K. Pułaskiego w Radomiu

Ul. Chrobrego 42/10, Radom, Polska

Tel: +48 504 174 290

email: kania6669@wp.pl

---

[1] Francuski matematyk, fizyk i astronom żyjący w latach 1749-1827.