Математическое моделирование движения зерновых смесей
по решетам помогает установить рациональную загрузку их рабочих
поверхностей при вибросепарировании. Поэтому теоретическое описание процесса
движения сыпучей среды по наклонной вибрирующей плоскости составило предмет
многих публикаций. Однако, наличие различных упрощений, в имеющихся
теоретических разработках, снижает их точность и ограничивает область
практической применимости, в связи с чем создание высокоточных и достаточно
универсальных математических моделей остаётся актуальной задачей.
Гармонические колебания слоя зерновой смеси на плоских
наклонных виброрешетах, как слоя вязкой жидкости, рассматривались в работах
[1,2]. В [1] теоретически исследован вибрационный режим движения
псевдоожиженной сыпучей среды при продольных гармонических колебаниях решета, а
в [2] – при поперечных. В обеих публикациях решалась краевая задача для
упрощённых уравнений Навье-Стокса, в предположении, что динамическая вязкость
псевдоожиженой зерновой массы является постоянной величиной. Такой подход
использовался авторами и в других работах [3,4]. Однако теоретическое
исследование псевдовязкости зерновой смеси в условиях вибраций показало, что
она зависит от распределения внутреннего давления в слое [3,5]. Поскольку
давление на частицу в плоском слое пропорционально глубине погружения её в
слой, то при строгой постановке задачи нужно учитывать эту зависимость. Поэтому
в данной работе рассмотрена динамическая модель, в которой описаны колебания
скорости потока зернового слоя как слоя неоднородной жидкости, вязкость которой
линейно зависит от поперечной координаты.
Целью статьи является вывод формул для расчёта
колебаний неоднородного потока зернового слоя по наклонным плоским виброрешетам.
В цель работы также входит исследование зависимости скорости, её градиента и
производительности от параметров вибраций решет и характеристик зерновой смеси.
Считаем, что слой смеси толщиной 
движется по
наклонному виброрешету вдоль координатной оси 
со скоростью 
, которая зависит от времени 
и поперечной
координаты 
. Координата 
перпендику-лярна
рабочей плоскости решета, состав-ляющей угол 
с горизонтом, как
показано на рис. 1.
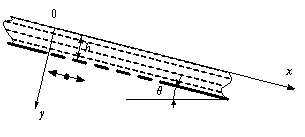
Рис. 1. Расчётная схема плоского виброрешета с
зерновым потоком
Решето совершает продольные колебания в своей
плоскости с амплитудой 
и частотой 
. В установившемся режиме движения скорость 
не зависит от
координаты 
и является решением
дифференциального уравнения:
(1)
при граничном условии:
(2)
В уравнении (1) 
- ускорение
свободного падения; 
- постоянный
множитель, характеризующий вибровязкость смеси и определяемый выражением [6]:
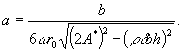(3)
Здесь 
; 
; 
- коэффициент
внутреннего трения в смеси; 
и 
- усреднённые радиус
и масса зерен в смеси, имеющей плотность 
.
Поскольку динамический коэффициент вибровязкости 
является линейной
функцией 
:
то
ограниченность производной 
при 
приводит к
“автоматическому” удовлетворению условию отсутствия касательных напряжений:
(4)
на
свободной поверхности слоя. Поэтому дополнительным к (2) граничным условием
является ограниченность 
и её производной по 
при 
Учитывая линейность уравнения (1), его решение
представим суммой двух слагаемых
, (5)
которые
удовлетворяют дифференциальным уравнениям:
; (6)
; (7)
и граничным условиям:
; 
(8)
Ограниченным вместе с производной при 
решением краевой
задачи для уравнения (6), является:
(9)
Решение уравнения (7) ищем в комплексной форме:
(10)
где
, 
- неизвестная
комплексная функция 
.
Подставив
(10) в (7), получаем:
(11)
Общее решение уравнения (11) выражается через функции
Кельвина и имеет вид:
(12)
Здесь 
; 
- произвольные
вещественные постоянные.
Функция 
сингулярная при 
. Поэтому 
и 
будут ограничены при 
, когда 
Учитывая эти значения
констант, а также (10) и (12), находим:
(13)
Граничное
условие (8) будет выполнено, если
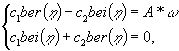(14)
Решив
систему (14), находим постоянные:
;
(15)
Таким образом, изменение скорости потока смеси по 
и 
описывается
выражениями (5), (9), (13) и (15).
Значения функций Кельвина можно определять по
таблицам, опубликованным в [7], [8] и других изданиях по специальным функциям.
Расчёт скорости существенно упрощается на свободной
поверхности слоя. Поскольку 
, 
, то
.
В высокочастотном режиме колебаний решета, когда 
, функции Кельвина аппроксимируются асимптотическими
выражениями [7]:
; 
,
в которых
;
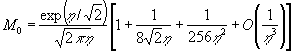Для такого режима вибраций решета скорость потока на
свободной поверхности 
приближённо
описывается элементарными функциями:
(16)
Подчеркнём, что знаменатель 
в (16) возрастает с
увеличением 
по показательному
закону, т.е. быстрее, чем числитель, пропорциональный 
. Поэтому в пределе:
.
Следовательно,
в высокочастотном режиме вибраций решета амплитуда колебаний скорости на
поверхности слоя очень мала, а скорость близка к постоянному значению.
Известно, что интенсивность сепарирования зависит от
процесса сегрегации смеси, который связан с градиентом скорости движения [3].
Поэтому далее рассмотрим вычисление этой характеристики. Продифференцировав
сумму (5) по 
, с учётом (9) и (13), получаем величину градиента:
. (17)
Здесь штрихом обозначены производные функций Кельвина
по 
. Таблицы этих производных опубликованы в [8]. Их можно
применять не только для вычисления величины градиента, а и касательного
напряжения 
по формуле (4).
Второй способ вычисления производных возможен на
основе формул [7]:
; 
,
поскольку таблицы функций
Кельвина индекса единица опубликованы в [7].
В формуле (17) возникает неопределённость типа 
при вычислении 
Чтобы раскрыть её,
воспользуемся пределами:
; 
Тогда
Определение градиента
на второй граничной плоскости зернового слоя можно упростить при высокочастотном
режиме колебаний решета. Из формул (15) и (17) при 
или 
следует, что
(18)
При больших 
, когда 
, имеет место асимптотика [7]:
;
;
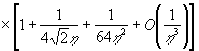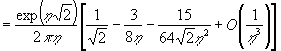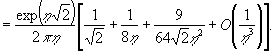
Используя её, вместо (18) получаем:
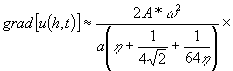
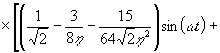
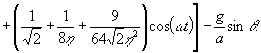(19)
Из последнего выражения видно, что амплитуды колебаний
возрастают с
увеличением 
и 
, т.е. увеличение амплитуды и частоты колебаний решета
сопутствует сегрегации смеси.
Определим далее удельную пропускную способность
(производительность) решета:
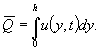(20)
При
вычислении интегралов учтём, что [7]:
;
(21)
;
Подставив сумму (5) в (20), на основании формул (9),
(13), (21), получаем:
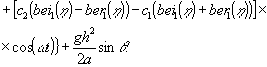(22)
Удельная пропускная способность решета зависит от
времени. Амплитуды её колебаний выражаются через затабулированные в [7] функции
Кельвина индекса единица.
При больших 
, когда 
, приближённый расчёт 
можно проводить с
помощью элементарных функций. Для этого следует учесть, что [7]:
; 
;
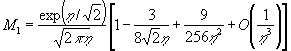Результаты расчётов и выводы. Расчёты проведены для
смеси проса [9] при следующих исходных данных: 
кг/м3; 
м; 
кг; 
м; 
; 
; 
м; 
с-1; 
с-1.
Вычисленные по (5) значения 
при различных 
графически показаны
на рис. 2-3, где цифрами 1,2,3,4 отмечены линии, соответствующие 
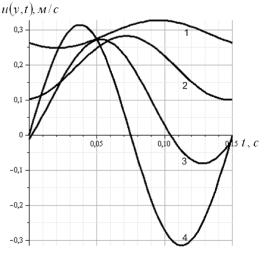
Рис. 2. Зависимости скорости колебаний зернового
потока проса при 
с-1: 1,2,3,4 - 
При 
амплитуды колебаний
скорости потока у поверхности решета больше, чем при 
. У свободной поверхности слоя амплитуды колебаний очень
малы, т.е. частицы движутся практически c постоянной скоростью. Эта скорость увеличивается с
увеличением частоты колебаний решета.
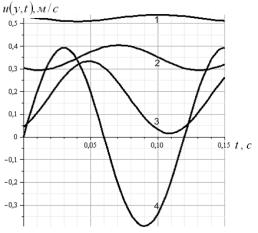
Рис. 3. Зависимости скорости колебаний зернового
потока проса при 
с-1: 1,2,3,4 - 
Исследуем изменение градиента по толщине слоя смеси
для разных моментов времени. На рис. 4 сплошной линией отмечена кривая,
рассчитанная по (17) для 
, точками - для 
и пунктиром – для 
при 
с-1. При 
градиент скорости
существенно меняется во времени.
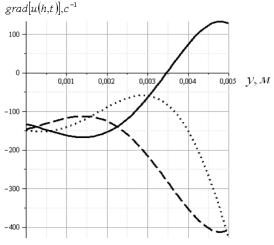
Рис. 4.Зависимости изменения градиента скорости
колебаний зернового потока проса для значений – - 
; 
- 
; --- 
;при 
с-1
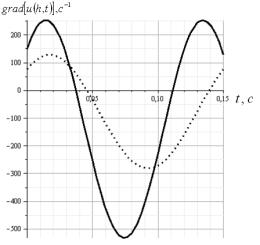
Рис. 5. Зависимости изменения градиента скорости
колебаний зернового потока проса при 
- 
с-1; – - 
с-1
На рис. 5 представлены результаты вычисления градиента
скорости у поверхности решета. Сплошной линией отмечена кривая, полученная для
значения 
c-1, а точками - для 
c-1.
Расчёты показывают, что величина градиента скорости у
свободной поверхности 
почти постоянна.
Колебания градиента скорости наибольшие у плоскости решета. Они быстро затухают
по мере приближения к свободной поверхности слоя.
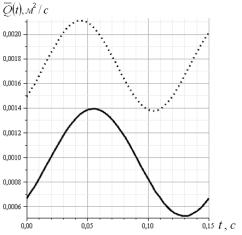
Рис. 6. Зависимости амплитуды колебаний удельной
производительности решета: – - 
с-1; 
- 
с-1
Результаты вычисления 
по формуле (22)
графически представлены на рис. 6. Сплошной линией отмечена кривая, полученная
для значения 
c-1, а точками - при 
c-1.
Пропускная способность решета колеблется около среднего значения:
С увеличением 
уменьшается параметр 
. Поэтому увеличение частоты колебаний решет повышает среднюю
пропускную способность.
Установленные закономерности изменений амплитуд
колебаний скорости, градиента скорости неоднородного зернового потока, удельной
производительности определяют эффективность процесса сепарирования с учётом
параметров вибрации плоских наклонных решёт и физико-механических свойств
смесей.
Литература
1.
Тищенко
Л.Н., Ольшанский В.П., Ольшанский С.В. К расчёту движения зерновой смеси на вибрирующем
плоском наклонном решете // Вібрації в техніці та технологіях, 2009. - №1. – С.
109-113.
2.
Тищенко
Л.Н., Ольшанский В.П., Ольшанский С.В. О влиянии поперечных колебаний плоского
наклонного решета на движение сепарируемой зерновой смеси // Праці Таврійського
державного агротехнологічного університету. – Мелітополь: ТДАТУ, 2009. – Вип. 9,
Т.2. – С. 131-139.
3.
Тищенко Л.Н.
Интенсификация сепарирования зерна. – Харьков: Основа, 2004. – 224с.
4.
Тищенко
Л.Н., Ольшанский В.П., Ольшанский С.В. Применение уравнения Бернулли к расчёту
движения зернового слоя на плоском наклонном виброрешете // Вібрації в техніці
та технологіях, 2009. - № 3 (55). – С.
42-47.
5.
Тищенко
Л.Н., Абдуева Ф.М., Ольшанский В.П. Сравнение двух способов вычисления
коэффициента вибровязкости псевдоожиженной зерновой смеси при виброцентробежном
сепарировании // Вібрації в техніці та технологіях, 2008. - № 1. – С. 96-100.
6.
Тищенко
Л.Н., Кучеренко С.И., Ольшанский В.П., Зайцев О.Б. Модель однослойного движения
зерновой смеси по наклонному рифлёному решету // Сучасні напрямки технології та
механізації процесів переробних і харчових виробництв. Вісник ХНТУСГ. – Харків:
ХНТУСГ, 2008. – Вип. 74. – С. 28-39.
7.
Абрамовиц
А., Стиган И. Справочник по специальным функциям(с формулами, графиками и
математическими таблицами). – М. : Наука, 1979. – 832 с.
8.
Янке Е.,
Эмде Ф., Лёш Ф. Специальные функции. – М.: Наука, 1977. – 344с.
9.
Гортинский В.В., Демский
А.Б., Борискин Н.А. Процессы сепарирования на зерноперерабытывающих
предприятиях. – М.: Колос, 1980. – 304 с.