Установление рациональных режимов движения зерновой
смеси приводит к повышению интенсивности сепарирования зерна на
перерабатывающих предприятиях. В настоящее время достаточно развиты
математические модели, описывающие движение отдельной частицы на вибрирующей
поверхности без учета влияния на него соседних частиц, сыпучей среды.
Вычисленные по такой теории кинематические характеристики потока смеси могут
значительно отличаться от тех, что имеют место в реальных условиях
сепарирования зерна. Поэтому разработка уточненных математических моделей движения
сыпучей зерновой массы по вибрирующей плоскости, с учетом взаимодействия
частиц, относится к актуальным задачам.
Из фундаментальных, обобщающих публикаций, в которых
обстоятельно изучено движение отдельной частицы на вибрирующей поверхности,
отметим работы [1,2,3,4]. Заслуживают отдельного внимания также системные
подходы к описанию движения зерновой смеси с помощью уравнений динамики
гранулированной сыпучей среды [5,6,7]. Они базируются на численном решении
систем нелинейных дифференциальных уравнений. Более просты в математическом
отношении методы расчета, основанные на гидродинамической аналогии, согласно которой
движение слоя зерна в условиях вибраций описывается уравнениями течения вязкой
жидкости без учета зависимости плотности смеси от давления в слое [5,8,9,10].
Но в этих работах при решении системы уравнений Навье-Стокса, или вытекающих из
нее соотношений, ограничивались анализом режимов движения с постоянной
проекцией скорости потока по длине решета. В действительности, под действием
сил тяжести и сопротивления эта проекция является переменной величиной. Для
определения распределения средней скорости движения слоя по длине решета, в
рамках гидродинамической теории, естественно воспользоваться основным
уравнением гидравлики, что и определило цель работы.
Целью работы является получение компактных формул для
расчета распределения средней скорости потока и толщины слоя зерновой смеси по
длине решета путем решения уравнения Д.Бернулли.
Пусть движение слоя зерновой смеси толщиной 
происходит вдоль координатной
оси 
, направленной по сепарирующей плоскости, решета под углом 
к горизонту (см. рис.
1). Решето совершает продольные (по оси 
) гармонические колебания. От частоты и амплитуды этих
колебаний, а также физико-механических параметров зерновой смеси, зависит ее
коэффициент вибровязкости 
. Формула для вычисления 
имеется в работе
[10], в связи с чем ее здесь не приводим.
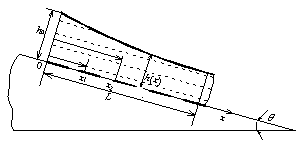
Рис. 1. Расчетная схема плоского наклонного виброрешета с зерновым
слоем
Для определения усредненной по толщине слоя скорости 
воспользуемся
уравнением Д.Бернулли, записанным относительно двух поперечных сечений слоя: 
и 
на интервале 
, где 
длина сепарирующей
плоскости решета:
. (1)
Здесь 
усредненная плотность
зерновой смеси; 
ускорение свободного
падения; 
и 
средние скорости и
давления в сечениях 
и 
; 
некоторые значения скорости
смеси в промежутке 
; 
толщина слоя смеси в
сечении 
, где зерно подается на сепарирующую плоскость.
Безразмерный коэффициент 
является аналогом
коэффициента линейных потерь напора в формуле Дарси-Вейсбаха [11].
Учитывая неопределенность значения 
в правой части (1),
заменим это уравнение его дифференциальным аналогом. Для этого положим:
; 
и устремим к нулю приращения 
и 
. Считая давление в смеси постоянным по длине решета 
, вместо (1) получаем дифференциальное уравнение:
. (2)
Начальным условием к уравнению (2) берем:
,
(3)
считая, что на сепарирующую плоскость слой смеси
попадает со средней скоростью 
. Таким образом, в исходных данных задаем параметры 
и 
, произведение которых равно удельной производительности
решета, приходящейся на единицу ширины сепарирующей плоскости.
Перед интегрированием уравнения (2) определим вид зависимости
.
Рассмотрим медленный, послойный режим движения смеси,
который соответствует ламинарному течению вязкой жидкости. Для такого режима в
гидравлике принимают [11,12]:
, (4)
где 
некоторая
положительная постоянная.
Подставив (4) в (2), путем разделения переменных и интегрирования,
с учетом условия (3), получаем:
.
Здесь 
. (5)
Выполнив интегрирование, находим:
. (6)
Чтобы получить в явном виде зависимость 
далее будем различать
случаи ускоренного и замедленного движений смеси.
При ускоренном движении, когда
,
уравнение (6) преобразуем к виду:
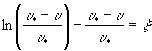, (7)
где 
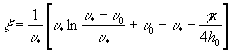. (8)
Решение уравнения (7) выражается через специальную
функцию Ламберта 
. Используя эту функцию, находим:
. (9)
Функция Ламберта отрицательного аргумента затабулирована
в работе [13, стр. 192]. Она отрицательна, поэтому 
. В пределе, когда 
, 
, 
:
. (10)
При замедленном движении, когда:
,
уравнение (6) сводим к виду:
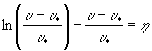, (11)
где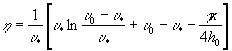 
. (12)
Скорость 
находим, решив
уравнение (11). Она также выражается через функцию Ламберта 
, но положительного аргумента. При замедленном движении смеси
имеем:
. (13)
Поскольку 
, а 
при 
, то и для этого случая движения имеет место предел (10).
Следовательно, как при ускоренном, так и при замедленном
движениях, скорость потока смеси стремится к граничному значению 
, которое напоминает скорость витания при падении твердого
тела в газовой среде.
Расчет 
связан с вычислением
функции Ламберта. Ее значения в области отрицательных аргументов можно находить
по таблице 7.3 из работы [13]. При отсутствии указанной таблицы на интервале 
удобно вычислять по
приближенной формуле:
,
погрешность которой меньше
0,5%.
В области положительных аргументов 
приближением функции
Ламберта является:
.
Погрешность этой аппроксимации также меньше 0,5%, что
приемлемо для инженерных расчетов.
При малых 
вычисление 
можно проводить с
помощью степенного ряда [14]:
.
Но ряд сходится только на промежутке 
.
При 
имеет место
асимптотика [15]:
,
в которой 
; 
.
На компьютере 
удобно вычислять в
среде «Maple» [16].
Из решения стационарной задачи гидродинамики о течении
вязкой жидкости по наклонному лотку известно, что [17]:
, (14)
где 
толщина движущегося
слоя жидкости на бесконечности, т.е. при 
.
Приравнивая выражения (5) и (14), получаем:
. (15)
Эта зависимость позволяет определять коэффициент 
теоретическим
способом, но для этого нужно знать значение 
. Последнее найдем, используя закон сохранения объема движущейся
смеси на единице ширины решета:
. (16)
Здесь 
скорость прохождения
проходовой фракции смеси через перфорированную поверхность решета с коэффициентом
живого сечения 
.
Из выражения (16) получаем
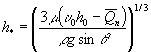. (17)
Определив по формулам (14), (15) и (17) параметры 
, 
, 
, далее не сложно рассчитать зависимость 
. Если окажется что 
, то движение смеси ускоренное и 
следует вычислять с
помощью (8) и (9). В случае, когда 
движение смеси
замедленное и 
описывается выражениями
(12) и (13).
С распределением скорости по длине решета связано также
распределение толщины движущегося слоя смеси, ибо по закону сохранения объема
зерна должно выполняться равенство:
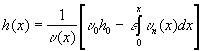. (18)
Если не учитывать отделение проходовой фракции от смеси,
то в выражениях (17) и (18) нужно положить 
; 
или 
.
Перед проведением расчетов конкретизируем зависимость 
и преобразуем формулы
(17) и (18). Предположим, что известно отношение объемов 
проходовой фракции 
и сходовой фракции 
, которые образуются в результате сепарирования смеси. Тогда
и для вычисления 
, вместо (17), получаем:
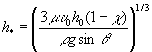. (19)
Далее аппроксимируем распределение скорости отделения
проходовой фракции по длине решета выражением
,
где 
положительная
постоянная, а 
.
Согласно этой аппроксимации максимум скорости отделения
проходовой фракции от смеси находится ниже середины решета по ходу движения
смеси, что наблюдается на практике. Учитывая, что
,
находим связь между константами 
и 
. В результате этого преобразования формулу (18) сводим к
виду:
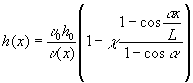. (20)
Расчет проводим в такой последовательности. По заданным
значениям 
и формулам (14), (19)
вычисляем 
и 
. Если окажется, что 
, то расчет 
проводим с помощью
выражений (8), (9). В случае когда 
, для расчета 
используем выражения
(12), (13). Распределение 
находим по формуле
(20).
Вычисления проведены при 
кг/м3, 
м; 
; 
м; 
. Рассматривали две частоты колебаний решета:
с-1 и 
с-1. Первой частоте соответствует 
Па×с, а второй – 
Па×с. На рисунках 2,3,4,5 цифрой 1 отмечены результаты
расчета для первой частоты, а цифрой 2 – для второй. Сплошные линии получены
при 
, а пунктирные – при 
.
На рис. 2 нанесены графики 
, представляющие распределение скорости потока смеси по длине
решета. Без учета отделения проходовой фракции 
графики оказываются
выше, чем с учетом отделения ее 
. Подача смеси на решето с начальной скоростью 
м приводит к
замедленному потоку зерна. Вследствие уменьшения скорости, с ростом 
на рис. 3 пунктирные
графики 
являются
возрастающими. Но при учете отделения сходовой фракции (сплошные линии) графики
возрастают лишь на
начальном, верхнем участке решета. Достигнув максимума, они начинают убывать,
поскольку уменьшается объем движущейся по решету смеси в результате прохождения
части зерна через перфорированную поверхность решета.
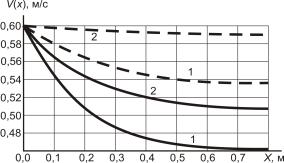
Рис. 2. Распределения
скоростей потока по длине решета при 
м/с
( 
; 
)
Рис. 3. Распределения толщины слоя смеси по длине
решета при 
м/с
( 
; 
)
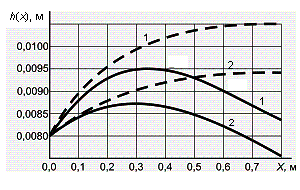
Аналогичные графики 
и 
представлены также на
рис. 4 и 5. Они получены при 
м и прежних остальных
параметрах. В отличие от предыдущего случая, здесь движение смеси ускоренное.
Оно сопровождается уменьшением 
по длине решета. Если
при 
убывает быстро
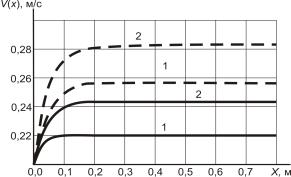
Рис. 4. Распределения
скоростей потока по длине решета при 
м/с
( 
; 
)
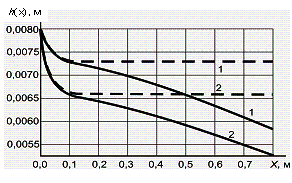
Рис. 5. Распределения толщины
слоя смеси по длине решета при 
м/с
( 
; 
)
лишь на начальном участке, а затем асимптотически
стремится к постоянному значению, то с учетом отделения проходовой фракции 
убывание толщины
движущегося слоя активно происходит по всей длине решета. Таким образом, учет
разделения фракций в ходе сепарирования существенно меняет распределение 
.
Выводы. Изложенная теория отражает основные
особенности движения сыпучего слоя зерна по наклонному решету. В зависимости от
скорости подачи смеси на решето, начальной толщины слоя и других параметров
поток зерна может быть ускоренным, равномерным или замедленным. Но это не
меняет заданной решету производительности.
Литература
1.
Василенко П.М. Теория
движения частицы по шероховатым поверхностям сельскохозяйственных машин. – К.:
УАСХН, 1960. – 284 с.
2.
Блехман И.И., Джанелидзе
Г.Ю. Вибрационное перемещение. – М.: Наука, 1964. – 410 с.
3.
Гортинский В.В., Демский
А.Б., Борискин М.А. Процессы сепарирования на зерноперерабатывающих предприятиях.
– М.: Колос, 1980. – 304 с.
4.
Заика П.М. Вибрационное
перемещение твёрдых и сыпучих тел в сельскохозяйственных машинах. – К.:УСХА,
1998. – 625 с.
5.
Тищенко Л.Н.
Интенсификация сепарирования зерна. – Харьков: Основа, 2004. – 224 с.
6.
Тищенко Л.Н., Пивень
М.В. К исследованию динамики зернового потока на наклонном решете // Підвищення
надійності відновлюємих деталей машин: Вісник ХДТУСГ. – Харків: ХДТУСГ, 2001. –
Вип. 8. Т. 1. – С.
198-205.
7.
Тищенко Л.Н., Миняйло
А.В., Пивень М.В., Харченко С.А. Исследование послойного движения зерновых смесей
на плоских вибрационных решетах // Механізація сільськогосподарського
виробництва: Вісник ХНТУСГ. – Харків: ХНТУСГ, 2007. – Вип. 59. Т. 1. – С.
69-76.
8.
Тищенко Л.Н., Абдуева
Ф.М., Ольшанс-кий В.П. О решениях упрощенных уравнений Навье-Стокса в
гидродинамической модели движения зерновой смеси // Механізація
сільськогосподарського виробництва: Вісник ХНТУСГ – Харків: ХНТУСГ, 2008. –
Вип. 75. Т.1. – С. 217 – 223.
9.
Тищенко Л.Н., Ольшанский
В.П. Решения упрощенных уравнений гидродинамики при моделировании движения
зерновой смеси по наклонному плоскому решету // Сучасні напрямки технології та механізації
процесів переробних і харчових виробництв: Вісник ХНТУСГ. – Харків: ХНТУСГ,
2008. – Вип. 74. – С. 306-312.
10.Тищенко
Л.Н., Кучеренко С.И., Ольшанский В.П., Зайцев О.Б. Модель однослойного движения
зерновой смеси по наклонному рифленому решету // Сучасні напрямки технології та
механізації процесів переробних і харчових виробництв: Вісник ХНТУСГ. – Харків:
ХНТУСГ, 2008. – Вип. 74. – С. 28-39.
11.Левицький
Б.Ф., Лещій Н.П. Гідравліка. – Львів: Світ, 1992. – 340 с.
12.Константінов
Ю.М., Гіжа О.О. Технічна механіка рідини і газу. – К.: Вища школа, 2002. – 277
с.
13.Кучеренко
С.І., Ольшанський В.П., Ольшанський С.В., Тіщенко Л.М. Балістика крапель, які
випаровуються при польоті. – Харків: ХНТУСГ, 2007. – 304 с.
14.Fariel Shafee.
Lambert function and new non-extensive form of entropy // IMA Journal of
Applied Mathematics, v. 72, 2007, p. 785-800.
15.Corless R.M.,
Gonnet G.H., Hare D.E.G., Jeffrey D. J. and Knuth D.E. On the Lambert W
Function // Advances in Computational Math. v. 5, 1996, p. 329-359.
16.Дьяконов
В.П. Марle 8 в математике, физике и образовании. – М.: Солон-Пресс, 2003. – 656
с.
17.Лойцянский
Л.Г. Механика жидкости и газа. – М.: Наука, 1973. – 847 с.