12rusnauka_9

к.ф.-м.н. И.А. Долгарев

 

КРАТКИЙ ОЧЕРК РАЗВИТИЯ

НЕКОММУТАТИВНОЙ ОДУЛЯРНОЙ ГАЛИЛЕЕВОЙ ГЕОМЕТРИИ

           

Геометрия пространства-времени Галилея очень молода по сравнению с евклидовыми геометриями. Появление различных галилеевых геометрий укрепляет статус  галилеевой геометрии. Аксиоматика Г.Вейля универсальна в геометрических исследованиях, является основой многих коммутативных, линейных, нелинейных, некоммутативных геометрий. Одулярные методы позволили хорошо продвинуться в изучении галилеевой геометрии, построить аналитическую и дифференциальную геометрии и разрешить классические геометрические задачи в новых условиях. Некоммутативные галилеевы геометрии делают полной картину описания предельного случая геометрии теории относительности. Одулярная галилеева геометрия относится к фундаментальной матматике.

Ниже приведены сведения по истории геометрии Галилея и о появлении некоммутативной одулярной галилеевой геометрии.

 

Изучение одулярной галилеевой геометрии осуществляется последние треть века. В настоящее время в этом направлении опубликовано более 90 работ различных авторов. На многих научных семинарах и конференциях обсуждаются вопросы указанной геометрии. В основе одулярных галилеевых геометрий лежат разрешимые действительные одули Ли и аксиоматика Г. Вейля аффинного пространства, в которой линейное пространство заменено одулем Ли.

            Одулярные галилеевы геометрии определены в схеме Г.Вейля. Аксиоматика Германа Вейля в геометрии опубликована в 1918 году (русский перевод [1]), тесно связана со специальной теорией относительности А. Эйнштейна. Сформулирована аксиоматика для аффинного пространства [1, с. 27 - 28] размерности . Метризация аффинного пространства достигнута посредством введения скалярного произведения векторов [1, с. 38 - 45]. Рассматриваются евклидово и псевдоевклидовы скалярные произведения векторов без дефектов. Почти одновременное появление книги Д. Гильберта по основаниям геометрии, (русский перевод [2]), вызвало всплеск интереса к аксиоматике Евклида в его «Началах», аксиоматика Г. Вейля оказалась в тени. Лет через 30-40 стала ясной универсальность аксиоматики Г. Вейля в построении многих геометрий, в том числе и римановой, [3]. Во второй половине прошлого века аксиоматика Г. Вейля заняла уверенные ведущие позиции, введена в учебные программы вузов, см., например, [4].

            В учебниках по геометрии для средней школы академик А.Н. Колмогоров интерпретировал вектор как параллельный перенос, [5], т.е. как одно из видов геометрических преобразований. Значит, действительное линейное пространство рассматривается как алгебраическая структура геометрических преобразований с внутренней операцией и связанной с ней внешней операцией умножения преобразований на действительные числа. Относительно внутренней операции – композиции преобразований, естественно, структура геометрических преобразований является группой, и более того – группой Ли. Становится интересным выяснить, какая геометрия возникает при рассмотрении других групп преобразований вместо группы параллельных переносов. Выбрав одуль Ли геометрических преобразований, отличный от линейного пространства, можно развивать в аксиоматике Г. Вейля геометрию пространства с выбранным одулем Ли.

            Близкой к группе параллельных переносов является группа параллельных переносов и гомотетий аффинного пространства (группа дилатаций). В преобразованиях этой группы всякая прямая аффинного пространства отображается на параллельную ей прямую. А преобразование, в котором любая прямая отображается на параллельную ей прямую, является либо параллельным переносом, либо гомотетией. Определив произведение переносов и гомотетий на действительные числа, получаем одуль Ли, называемый растраном (одуль Ли расширений и трансляций). Первая публикация по геометрии пространства с растраном относится к 1986 году, [6], неметризованное пространство с растраном называется ЛМ-пространством. В [6] растран определен абстрактно, приведена его аксиоматика, довольно громоздская, содержащая более 20 аксиом. Вместе с тем указана модель растрана. В дальнейшем аксиоматика растрана совершенствуется и в [7] приведена система аксиом растрана, состоящая из трёх аксиом. Первое сообщение о растране и начальных свойствах ЛМ-пространства сделано А.И. Долгаревым в 1983 году на научном семинаре кафедры геометрии Красноярского пединститута. С 1984 года А.И. Долгарев участвует в Герценовских чтениях в Ленинградском пединституте, в секции геометрии.

С учетом своеобразия растрана введена галилеева норма растов (элементов растрана) и дифференцирование растранных функций, что дало возможность изучать дифференциальную геометрию пространства с растраном. Пространство с метризованным растраном называется ЕМ-пространством. Растран является некоммутативной структурой, геометрии ЛМ- и ЕМ-пространств некоммутативны и как некоммутативная геометрия является гиперболической по взаимному расположению прямых.

            В 1985 году А.И. Долгаревым сделаны сообщения о геометрии ЛМ- и ЕМ-пространств на семинаре профессора Б.А. Розенфельда в Московском пединституте им. В.И. Ленина и на семинаре им. Н.И. Лобачевского в Казанском университете им. В.И. Ульянова-Ленина. В Красноярске, Ленинграде и Москве сообщения автора по некоммутативной геометрии вызывали большой интерес. Сообщение на семинаре в Казани вызвало явно выраженную отрицательную реакцию. Автору посоветовали взамен заняться геометрией групп Ли, отличающейся от одулярной геометрии, посчитав одулярную геометрию неприемлемой.

            Одулярная галилеева геометрия является разделом фундаментальной математики. Она близка к геометрии групп Ли, с большой натяжкой может считаться галилеевой геометрией групп Ли, [8]. Как в геометрии групп Ли, так и в одулярной галилеевой геометрии основой являются группы Ли и векторная аксиоматика Г.Вейля. Общеизвестно, например, что абелевы группы и модули над кольцом (в частности, линейные пространства над полем) являются различными алгебраическими структурами. Точно также группа Ли и действительный одуль на группе Ли различные структуры. Как абелева группа Ли (на которой определено линейное пространство над полем действительных чисел) имеет очень простую структуру. Но геометрия пространств, обладающих линейным пространством, очень содержательна и многообразна. Она включает в себя аффинную геометрию, геометрии пространств со скалярным произведением векторов (евклидову, псевдоевклидову и др.), развивается синтетически и аналитически, использует методы дифференциального и интегрального исчисления, теорию поля и т.д.; разработаны результативные методы исследования – методы дифференциальной геометрии, тензорные, внешнего дифференцирования и др. Переходя к некоммутативным одулям Ли невозможно надеяться на положительный итог использования коммутативных дифференциально-геометрических методов в некоммутативном случае. Применяемые идеи классических методов исследования претерпевают в результате адаптации к новым условиям кардинальные изменения. Простота устройства отделтных групп Ли, на которых определены одули Ли, не влечет простоты одулярных геометрий, напротив, геометрическая теория усложняется по сравнению с классической геометрией пространств, использующих векторные и тензорные методы.

            В геометрии групп Ли другие методы исследований, использующие структуру алгебры Ли дифференцирований. Одулярная галилеева геометрия развивает методы классической дифференциальной геометрии, одулярного анализа, что кардинально отличает одулярную геометрию от геометрии групп Ли. Если даже не брать во внимание различие структур группы Ли и одуля Ли, то различие методов исследования незаметить невозможно. В работах по одулярной галилеевой геометрии построена аналитическая и дифференциальная галилеева геометрия.

В 1988 году опубликованы тезисы [9] о кривых ЕМ-пространства в материалах IX Всесоюзной геометрической конференции. Реакцией на тезисы было личное письмо Л.В. Сабинина автору, в котором он обосновывал, что растран это частный вид одуля над кольцом, пространства с растраном относятся к одулярным пространствам. Развивая дифференциальную геометрию ЕМ-пространства, А.И. Долгарев подготовил кандидатскую диссертацию [10], которую защитил в 1991 году в совете университета Дружбы Народов в Москве. Научным руководителем указанной диссертации является д.ф.-м.н., профессор Л.В. Сабинин.

В дальнейшем выяснилось, что существует несколько видов растранов, [11]. Построена конечная ЛМ-плоскость (с растраном), [12], плоскости с растраном наименьшего порядка,  [13], в том числе и метрическая.

            В некоммутативной геометрии пространства с растраном взаимное расположение прямых является гиперболическим, аналогичным взаимному расположению прямых на плоскости Н.И. Лобачевского. Всякие три неколлинеарные точки ЛМ-пространства определяют единственную плоскость, ЛМ-пространство содержит и аффинные плоскости: через всякую точку проходит единственная аффинная плоскость. Уравнения прямых и плоскостей нелинейны в общем случае. Правила дифференцирования растранных функций отличны от правил дифференцирования векторных функций. Дифференциальная геометрия ЕМ-пространства развивается по аналогии с дифференциальной геометрией евклидова пространства. Результаты получены аналогичные, хотя геометрия некоммутативная и галилеева. Оба эти фактора значительно усложняют полученную теорию.

            Таким образом, аксиоматика Г. Вейля является общей для геометрий коммутативных аффинного и евклидовых пространств и некоммутативных одулярных пространств, т.е. для гиперболических пространств. Имеются работы [14, 15], в которых начаты исследования по коммутативным и нелинейным геометриям в аксиоматике Г. Вейля.

 

            Исследования геометрии пространства-времени Галилея ведутся с начала XX века. Историю этих исследований можно найти в [16 – 19]. Обстоятельная популярная книга [19] в 2002 году переведена на английский язык и издана в США. К первым  работам, связанным с принципами относительности А. Эйнштейна и Г. Галилея, относится статья Л. Бервальда [20], 1915 год, также работа Л. Зильберштейна [21], 1925: работа [22] А.П. Котельникова из Казани, 1927 год. Впервые на связь геометрии Галилея с классической механикой Галилея-Ньютона указал П.А. Широков [23], 1917. Свое название геометрия Галилея получила по связи с принципом относительности Галилея. Геометрия плоскости Галилея изучалась С. Гласом [24], 1925. Особенно подробно плоскость Галилея исследовала Н.М. Макарова в 1956 – 1957 годах. Первая кандидатская диссертация по геометрии плоскости Галилея защищена Н.М. Макаровой, [25], 1962 год. Галилеево скалярное произведение векторов впервые введено А.И. Долгаревым в 2003 году в [26], где изложена дифференциальная геометрия 3-мерного пространства-времени Галилея.  Геометрия Галилея относится к многочисленным геометриям пространств со скалярным произведением векторов, т.е. к евклидовым геометриям. В 2006 году опубликована монография [27], посвященная одулярной галилеевой геометрии пространств с разрешимыми 3-мерными одулями Ли и некоторым специфическим вопросам одулярной геометрии.

            До работы [27] рассматривалась галилеева метрика – галилеево расстояние между точками, определение см. в математической энциклопедии, т.1, с. 843. Это  расстояние задается двумя равенствами. Если  и  точки (два события) пространства-времени Галилея,  вектор,  = , то расстояние между точками  и  есть:

 =

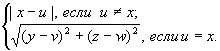
Согласно Б.А. Розенфельду, [18, c. 41], оно относится к квазиметрикам. В [27], галилеево скалярное произведение векторов  и  определено равенствами:

 =

В 3-мерном пространстве-времени Галилея доказана основная теорема теории кривых, [28], основная теорема теории поверхностей доказана в [29]. Арнольд В.И. рассматривает пространство-время Галилея , , как прямую сумму мерного евклидова пространства  и оси времени , [30, c. 11 – 14], но геометрию Галилея не развивает. Целью книги [30] является анализ положения дел в решении задачи И. Ньютона об отыскании траекторий движения материальной точки в заданном поле ускорений движения. В начале книги [30, с. 26] в аннотации к § 5 В.И. Арнольд констатирует, что современная математика бессильна в решении задачи И. Ньютона для движения с двумя степенями свободы. Задача И. Ньютона есть задача классической механики Галилея-Ньютона, видимо для ее решения естественно использовать методы геометрии Галилея. Однако, эти методы ко времени написания книги [30] небыли развиты. Решение задачи И. Ньютона галилеевыми методами дано в [31, 32].

Геометрией Галилея называется та классическая теория пространства-времени с 1-мерным временем, которую начали развивать П.А. Широков и А.П. Котельников в [23, 22] и которая коммутативна. Другие геометрии с галилеевой метрикой называются галилеевыми, к ним относятся и одулярные некоммутативные галилеевы геометрии.

Начато изучение 4-мерного пространства-времени Галилея [33 – 35]. По начатым исследованиям видно, что в изучении многомерных галилеевых пространств ожидаются большие трудности.

            С развитием геометрии пространства с растраном возник интерес к другим геометриям в схеме Г.Вейля c одулями Ли аффинных преобразований. Одули на произвольной алгебраической структуре с одной внутренней бинарной операцией в 1977 году определил российский математик Л.В. Сабинин, [36]; одули Ли ввел А.И. Долгарев, [27]. (Заметим, что в Новосибирском университете, где работал Л.В. Сабинин, выплачивают стипендию им. Сабининна студентам и магистрантам.)  В [37] определен 3-мерный нильпотентный одуль Ли над полем  действительных чисел – одуль Ли галилеевых движений плоскости, названный сибсоном. Галилеевы движения составляют пододуль в аффинном одуле Ли, он является одним из расширений мультипликативного одуля дуальных чисел.

            В [38] дано  одулярное описание аффинных преобразований действительной аффинной плоскости. Появился интерес к одулям аффинных преобразований плоскости – к пододулям аффинного одуля. В [39] опубликованы операции на многообразии , задающие некоторые разрешимые группы Ли; операции получены С.П. Гавриловым из Казанского университета. Это позволило А.И. Долгареву написать операции на многообразии , определяющие все 3-мерные разрешимые группы Ли и затем получить внешние операции умножения элементов этих групп на действительные числа, [27]. Существуют следующие 3-мерные коммутативные одули Ли: линейное пространство, альтернативные линейные пространства – линейные пространства с нелинейными коммутативными операциями, аналогичными операциям из [14]. Существует несколько видов растранов, сибсон, диссон, осцилляторный одуль. Этим исчерпываются разрешимые пододули одуля Ли аффинных преобразований плоскости. Диссон является еще одним расширением (наряду с сибсоном) мультипликативного одуля дуальных чисел. Осцилляторный одуль есть одуль евклидовых движений плоскости. Но выяснилось, что осцилляторные функции недифференцируемы, [40]. Следовательно, не существует одулярной дифференциальной галилеевой геометрии с осцилляторным одулем.

В этом существенное отличие одулярной геометрии от геометрии групп Ли, созданной Э. Картаном в начале прошлого века. В геометрии Картана рассматриваются все группы Ли без исключения. Этот факт говорит лишний раз о том, что одулярная галилеева геометрия не является частью геометрии групп Ли, которая вообще не изучает случай галилеевых пространств.

Описаны конечные сибсоны ступени нильпотентности 2, [41], они многомерны; можно развивать многомерные нильпотентные одулярные геометрии.

            3-мерная некоммутативная галилеева геометрия с сибсоном излагается в [42 – 44], такая же геометрия с диссоном содержится в [45, 46]. Изложение геометрий галилеевых ВО-пространств имеется в [27]. Работы [45 – 49, 28]  посвящены некоторым качественны критериям для кривых и поверхностей ВО-пространств, дифференциальным уравнениям их поверхностей.

Свойства пространств с одулями Ли зависят от алгебраических свойств их одулей. 3-мерный растран, как и линейное пространство, порождается тремя элементами, остальные некоммутативные 3-мерные одули Ли порождаются двумя одулярами. Во всяком ВО-пространстве через две различные точки проходит единственная прямая. В некоммутативном пространстве через точку вне прямой проходит две прямые, параллельные данной прямой. В пространстве с растраном через всякие три неколлинеарные точки проходит единственная плоскость. Существуют плоскости с 2-мерными растранами – 2-мерные пространства с растраном. Других 2-мерных пространств с некоммутативными одулями Ли не существует. В пространствах с сибсоном, диссоном и осцилляторным одулем существуют неколлинеарные точки, не лежащие ни в какой плоскости. Уравнения прямых и плоскостей ВО-пространства нелинейны. В каждом некоммутативном метризованном пространстве через всякую точку проходит единственная евклидова плоскость. Много общего у евклидовой геометрии и геометрии пространства с растраном. В пространствах с сибсоном и с диссоном регулярная кривая не обладает соприкасающейся плоскостью; поверхности не обладают касательной плоскостью. Определены кривизна и кручение кривых; по заданным функциям кривизны и кручения во всяком ВО-пространстве кривая определяется однозначно, [28]. Определены первая и вторая квадратичные формы поверхностей, полная и средняя кривизны поверхностей.

Коэффициенты первой и второй квадратичных форм поверхности однозначно определяют поверхность, [50 , 51]. Полная кривизна поверхности только в пространстве с растраном относится к внутренней геометрии поверхности. Свойства ВО-пространств с одулями Ли аффинных преобразований связаны и со свойствами аффинных преобразований. При этом полезна работа [52], хотя и использующая другие методы исследований. Идеи из этой работы важны в определении геометрических понятий. Одулярные методы хороши при отыскании траекторий преобразований [53], траектории занимают в [53]  заметное место.

Галилеевы пространства с 2-мерным временем рассматриваются в [54 – 56]. Определены гиперболические галилеевы плоскости, [57, 58]. На Колмогоровских чтениях в Тамбовском университете рассматривается плоскость Лобачевского-Галилея, т.е. гиперболическая галилеева плоскость; гармонические функции на этой плоскости. Имеются работы других авторов по одулярным геометриям, [14, 15, 29, 35, 48, 55 – 61].

 

            Рассматриваются также альтернативная аффинная плоскость [15], альтернативная плоскость Галилея [68], поверхности в альтернативном 3-мерном галилеевом пространстве [65]. Это элементы нелинейной коммутативной геометрии. Нелинейные структуры вызвали у математиков некоторый интерес.  В одном из разделов монографии [67, с. 237 - 261] профессор А.И. Хубежты  изложил «альтернативную аффинную плоскость Долгаревых», (см. [12, 13]).

            Разработано приложение галилеевых методов в евклидовой геометрии [68, 31], что существенно упрощает некоторые сложные вопросы евклидовой геометрии. Вводятся галилеевы натуральные уравнения евклидовой кривой, галилеевы квадратичные формы евклидовой поверхности; намечается развитие неоднородной евклидовой геометрии, в частности, геометрии пространства с эклиптикой.

Геометрии некоммутативных галилеевых одулярных пространств в аксиоматике Г. Вейля соединяют в себе идеи изучения пространства-времени, идеи некоммутативности в геометрии и идеи расширения применения схемы  Вейля. Осуществление каждой из указанных идей с возрастанием размерности вызывают большие трудности, но является назревшей необходимостью. В некоммутативной геометрии имеется несколько направлений. Одно из них возникло в физике, оформлено А. Коном, [69]. Считается, что некоммутативная геометрия началась со статьи Гайзенберга об атомных спектрах, т.е. с потребностей физики. В 2001 году А.Кон получил премию Крафурда за создание некоммутативной геометрии. В МГУ профессор А.С. Мищенко руководит семинаром по некоммутативной геометрии, которая близка к теории А.Кона.  А.И. Долгарев изучает с 1983 года одулярные некоммутативные геометрии. Многоплановость некоммутативной геометрии говорит о ее большой востребованности.

Некоммутативность геометрии не настолько необычна, как может показаться. Известна аксиоматика евклидовой геометрии, предложенная в конце 19 века М. Пиери, учеником Пеано, в которой к основным понятиям геометрии относятся движения. Группа евклидовых движения некоммутативна. Это дает основание считать евклидову геометрию некоммутативной. В книге Ф. Бахмана [70] дается построение многих геометрий (в том числе евклидовой, Лобачевского) на основе понятия симметрии, чем устанавливается некоммутативность этих геометрий.

Структура галилеевых пространств описывается в [71]. Пространство-время Галилея является предельным случаем пространства-времени в специальной теории относительности (СТО): если скорости движущихся объектов в пространстве-времени малы по сравнению со скоростью света, то формулы Лоренца превращаются в формулы Галилея. Пространство-время Галилея является предельным случаем псевдоевклидова пространства. Структура пространств в СТО и ОТО (общей теории относительности) описывается в [3, c. 615 – 639]. Геометрия пространств в СТО псевдоевклидова и плоская, а в ОТО псевдориманова и искривлена. Множество одновременных событий в СТО является евклидовым подпространством, а в ОТО не составляет подпространства в псевдоримановом пространстве. Популярное изложение этих вопросов содержится в [72, c. 37 - 38]. Пространству-времени в СТО  соответствует пространство-время Галилея, пространству-времени в ОТО соответствуют некоммутативные одулярные галилеевы пространства, которые искривлены [73].

 

Список литературы

      1.  Вейль Г. Пространство. Время. Материя. Лекции по общей теории относительности.

          – М.: Едиториал УРСС, 2004. – 456 с.

      2.  Гильберт Д. Основания геометрии. -М.-Л., 1948. -492 с.

  1. Рашевский П.К. Риманова геометрия и тензорный анализ. - М.: Наука, 1967. -664с.
  2. Базылев В.Т. и Дуничев К.И. Геометрия. II. – М.: Просвещение, 1975. – 367с.
  3. Колмогоров А.Н., Семенович А.Ф., Черкасов Р.С. Геометрия 6 – 8 . – М.: Просвещение, 1974. – 384с.

6.      Долгарев А.И. ЛМ-пространство.//Римановы пространства и методы эллиптических дифференциальных уравнений.  Л.: ЛГПИ, 1986. - С. 8 - 25.

7.      Долгарев А.И. Растран в алгебре, геометрии, физике. Одулярная геометрия. // Iнтегральнi перетворення та їx застосування до крайових задач,  Зб. наук. пр., - Київ: Iн-т математики НАН України, 1997, вип. 16. - С. 96-108.

8.      Картан Э. Геометрия групп Ли и симметрические пространства. – М.: ИЛ – 1949. – 386 с.

9.      Долгарев А.И. Кривые ЕМ-пространства// IX Всесоюзная геометрическая конф., труды. участн. – Кишинев, 1988. – С. 100.

10.  Долгарев А.И. ЕМ-пространства. Дис... канд. физ.-мат. наук, Красноярск: КГПИ, 1991.-95 с.

  1. Долгарев, А.И. Растраны на различных структурах.- Киев: Ин-т математики НАН Украины, 1996. – 106 с.
  2. Долгарев А.И., Анисимова О.И., Кирсанов Р.В., Сергеевев М.В. Конечная ЛМ-плоскость// Математика и информатика: Межвуз. сб. - Пенза: ПГПУ им. В.Г.Белинского, 1996, С. 12-17.
  3. Долгарев А.И. Плоскости с растраном наименьшего порядка. – Materiali VIII Miedzynarodowej naukowi-praktycznej konferenceji “Naukowa mysl informacyjnej powieki – 2012.” Volume 28. Przemysl. 2012, p. 3 – 13.
  4. Долгарев А.И., Долгарев И.А. Альтернативное 2-мерное действительное линейное пространство. Группа Ли замен базисов пространства.// Владикавказский математический журнал – Владикавказ, 2008, Т.10, вып. 2. – С. 9 – 20.
  5. Долгарев А.И., Долгарев И.А. Альтернативная аффинная плоскость.// Влади-кавказский математический журнал – Владикавказ, 2007, Т.9, вып. 4. – С. 4 – 14.

16.  Розенфельд Б.А. История неевклидовой геометрии. – М.: Наука, 1976, 408с.

17.  Розенфельд Б.А. Неевклидовы пространства. – М.: Наука, 1969. – 548с.

  1. Розенфельд Б.А., Замаховский М.П. Геометрия групп Ли. Симметрические, параболические и периодические пространства. – М.: МЦНМО, 2003.- 560с.
  2. Яглом И.М.  Принцип относительности Галилея и неевклидова геометрия. М., Наука,  1969. с.304

20.  Berwald L. Uber Bewegungsinvarianien und elementare Geometrie in der Minimalebene.// Monatshelfe fur Math. Und Phys. 26 (1915), p. 211 – 228.

21.  Silberstein L. Projective geometry of  Galileian space-time.//  Philos. Magazin 10 (1925), p. 681 – 696.

22.  Котельников А.П. Принцип относительности и геометрия Лобачевского.// Сборник  «In memorial Lobatschevskii», вып. 2, Казань: Главнаука, 1927. – С. 37 – 66.

23.  Широков П.А. Интерпретации и метрика квадратичных геометрий. В кн. П.А. Широков. Избранные труды по геометрии. Казань: КГУ, 1966 - С. 15 – 179.

24.  Glass S. Sur les geometries de Cayley et sur une geometrie plane particuliere.// Annales de la Soc. Pol de Math., f. 5, 1926, p. 20 – 36.

  1. Макарова Н.М. Двумерная неевклидова геометрия с параболической метрикой длин и углов: Дис. ... канд.физ.-мат.наук. - Л., 1962.
  2. Долгарев А.И.  Элементы дифференциальной галилеевой геометрии и одуль галилеевых преобразований. – Саранск: Средневолжское математическое общество, 2003, препринт 63. – 116с.
  3. Долгарев А.И. Классические методы в дифференциальной геометрии одулярных пространств. Монография. – Пенза: ИИЦ ПГУ, 2005.- 306с.

28.  Долгарев А.И. Натуральные уравнения кривых 3-мерных одулярных галилеевых пространств// Дифференциальная геометрия многообразий фигур. Межвуз. тем. сб. научн. тр. Вып. 36. – Калининград: КГУ, 2005. – С. 31 – 36.

29.  Долгарев И.А. Нахождение поверхности в 3-мерном пространстве-времени Галилея по ее квадратичным формам.// Известия высших учебных заведений. Поволжский регион. Сер. Естественные науки,  № 5, Пенза: ИИЦ ПГУ, 2006, С. 51 – 60.

  1. Арнольд В.И. Математические методы классической механики. – М.: Наука, 1989.  – 472с.

31.  Долгарев А.И. Методы одулярной галилеевой геометрии в описании механических движений.// Известия высших учебных заведений. Поволжский регион. Физико-математические науки, Пенза: ИИЦ ПГУ,  2007, № 3, с. 12 – 24.

  1. Долгарев А.И. Решение задачи Ньютона для движения с тремя степенями свободы.- Materialy VIII mezinarodni vedecko-praktika conference “Veda a vznik – 2011 - 2012”. Dil 28. Matematika, Fizika, Moderni informacni  technologie. Praga, 2012, p. 3 – 8.

33.  Долгарев А.И., Долгарев И.А. Кривые 4-мерного пространства-времени Галилея. // Известия высших учебных заведений. Поволжский регион. Физико-математические науки, Пенза: ИИЦ ПГУ, 2007, № 3, с. 2 – 11.

34.  Долгарев А.И. Специальные вопросы теории кривых 4-мерного пространства–времени Галилея. // Известия высших учебных заведений. Поволж­ский регион. Физико-математические науки. -  Пенза ИИЦ ПГУ, 2008. - № 1. - С. 41-54.

35.  Долгарев И.А. Поверхности 4-мерногопространства-времени Галилея. Полная кривизна поверхности.// Известия высших учебных заведений. Поволжский регион. Физико-математические науки,  № 3(7), Пенза: ИИЦ ПГУ, 2007, С. 3 – 19.

  1. Сабинин Л.В. Одули как новый подход к геометрии со связностью // ДАН СССР. 1977. N5. C.800-803.

37.  Долгарев А.И. Дифференцирование одулярных функций // Iнтегральнi перетворення та їx застосування до крайових задач,  Зб. наук. пр., - Київ: Iн-т математики НАН України, 1995, вип. 10. - С. 57-79.

38.   Долгарев А.И. Одулярное описание аффинных преобразований плоскости. Деп. в ВИНИТИ 02.07.97, № 369 – 97. М. ВИНИТИ, 1997 – 97с.

  1. Левичев А.В. Однородная хроногеометрия. I. - Новосибирск: НГУ, 1991. - 52 с.
  2. Долгарев А.И. Недифференцируемый одуль. // Дифференциальная геометрия многообразий фигур, Межвуз. тем. сб. научн. тр., Калиниград, КГУ, 2001, вып. 32. - С. 34-37.
  3. Долгарев А.И. Описание конечных нильпотентных групп ступени 2 простого нечетного периода.// Известия вузов. Математика. – 2008. № 12, С. 17 – 27.
  4. Долгарев А.И. Дифференциальная геометрия пространства с касательным отображением в одуль галилеевых движений. – Саранск: Средневолжское математическое общество, 2002, препринт 51. –  52с.
  5. Долгарев А.И. Поверхности в дифференциальной геометрии пространства с касательным отображением в одуль галилеевых движений. – Саранск: Средневолжское математическое общество, 2003, препринт 62. – 40с.
  6. Долгарев А.И. Поверхности, аналогичные плоскостям в нильпотентном одулярном пространстве// Дифференциальная геометрия многообразий фигур,  Межвуз. тем. сб. научн. тр.,  Калиниград,  КГУ,  2003,  вып.  34. - С. 37-42.

45.  Долгарев А.И. Кривые в одулярной дифференциальной геометрии пространства на диссоне – Известия высших учебных заведений. Поволжский регион. Сер. Естественные науки, 2003, № 6(9), С. 43 – 49.

46.  Долгарев А.И. и Долгарев И.А.  Поверхности в ВО-пространстве с диссоном. – Известия высших учебных заведений. Поволжский регион. Сер. Естественные науки, 2005, № 6(19), С. 34 – 48.

47.  Долгарев А.И. Качественные критерии для кривых и поверхностей 3-мерных одулярных галилеевых пространств. 1. Критерии  для кривых. // Известия высших учебных заведений. Поволжский регион. Сер. Естественные науки, 2006, № 5(26), С. 27 – 41.

48.  Долгарев А.И., Долгарев И.А Качественные критерии для кривых и поверхностей 3-мерных одулярных галилеевых пространств. 2. Критерии для поверхностей.//  Известия высших учебных заведений.  Поволжский  регион.  Физико-математически  науки, Пенза, 2007,  № 1, С. 3 – 17.

  1. Долгарев А.И. Дифференциальные уравнения поверхностей одулярных пространств. Нормальная кривизна поверхности.// Труды  Средневолжского  математического  общества,     Саранск,   СВМО,  Т. 6,  № 1,  2004. –   С. 132 – 144.

50.  Долгарев И.А. Получение поверхности 3-мерного галилеева пространства с растраном по коэффициентам ее квадратичных форм. //  Известия высших учебных заведений.  Поволжский  регион.  Физико-математически  науки, Пенза, 2007,  № 6, С. 17 – 31.

51.  Долгарев И.А. Получение поверхностей одулярного галилеева пространства с сибсоном по коэффициентам их квадратичных форм.//  Известия высших учебных заведений.  Поволжский  регион.  Физико-математически  науки, Пенза, 2009,  №  2(10), С. 68 – 82.

  1. Широков П.А. и Широков А.П. Аффинная дифференциальная геометрия. – М., 1959. – 319с.

53.  Долгарев А.И. Одули Ли преобразований. Траектории и поверхности траекторий. Собственная геометрия поверхностей. – Известия высших учебных заведений.  Поволжский  регион.  Физико-математически  науки, Пенза,  2008,  № 2(6), С. 21 – 38.

  1. Долгарев А.И., Долгарев И.А. 3-мерное галилеево одулярное нильпотентное пространство с 2-мерным временем.// Гиперкомплексные числа в геометрии и физике. 1(9), том 5. М.: МГТУ им. Н.Э. Баумана, 2008. – С. 140 – 152.

55.  Долгарев А.И., Зелева Е.В. Растран с 2-мерным временем.// Известия высших учебных заведений. Поволжский регион. Физико-математические науки, Пенза: ИИЦ ПГУ, 2008, № 3(7), С. 20 – 29.

56.  Долгарев А.И., Зелева Е.В. Кривые 3-мерного галилеева пространства с растраном с 2-мерным временем.// Известия высших учебных заведений. Поволжский регион. Физико-математические науки, Пенза: ИИЦ ПГУ, 2009, № 1(9), с. 55 – 68.

  1. Долгарев А.И. Модели гиперболических плоскостей с псевдоевклидовым и галилеевым расстояниями между точками// Труды Средневолжского математического общества, Саранск, СВМО, Т. 5, № 1, 2003. – С. 262-266.

58.  Долгарев А.И. Гравитационная галилеева плоскость.// Известия высших учебных заведений. Поволжский регион. Сер. естественные науки, Пенза: ИИЦ ПГУ, 2005, № 6, С. 68 – 83.

59.  Долгарев А.И., Королева Ю.А., Липикина Е.А., Синицина О.В. Прямые и плоскостив 4-мерном пространстве-времени с W-сибсоном. // Известия высших учебных заведений. Поволжский регион. Физико-математические науки,  № 4, Пенза: ИИЦ ПГУ, 2007, С. 18 – 34.

  1. Долгарев А.И., Подвалова О.А. Кривые в галилеевых пространствах с 4-мерными растранами. // Известия высших учебных заведений. Поволж­ский регион. Физико-математические науки. – Пенза: ИИЦ ПГУ, 2009. - № 3. - С. 35 – 49.

61.  Долгарев И.А. Поверхности пространства-времени Галилея по символам Кристоффеля.// Известия высших учебных заведений. Поволжский регион. Физико-математические науки,  № 2(6), Пенза: ИИЦ ПГУ, 2008, С. 39 – 50.

62.  Валовик Д.В. Кривые в одулярной дифференциальной геометрии с растраном общего вида. // Известия высших учебных заведений. Поволжский регион. Физико-математические науки,  № 2, Пенза: ИИЦ ПГУ, 2007, С. 10 – 18.

63.  Долгарев А.И., Рябова Е.И. Кривые в галилеевом пространстве с 3-мерным V-растраном.// Известия высших учебных заведений. Поволж­ский регион. Физико-математические науки. -  Пенза ИИЦ ПГУ, 2009. - № 3(11). - С. 22 – 34.

  1. Долгарев И.А. Галилеевы квадратичные формы евклидовой поверхности. // Метрическая геометрия поверхностей и многогранников. Междунар. Конф., посв. 100-летию со дня рождения Н.В. Ефимова. Москва, 18 – 21 авг. 2010. Сборник тезисов. М.: МАКС Пресс, 2010. - С. 24 – 25.

65.  Долгарев И.А. Поверхности в коммутативной нелинейной геометрии 3-мерного пространства-времени Галилея.//Известия высших учебных заведений. Поволжский регион. Физико-математические науки,  № 1(9), Пенза: ИИЦ ПГУ, 2009, С. 69 – 86.

  1. Долгарев А.И., Долгарев И.А. Плоскость Галилея с коммутативной и нелинейной геометрией.// Владикавказский математический журнал – Владикавказ, 2010, Т.10, вып. 2. – С. 3 – 14.
  2. Хубежты И.А. Теория плоскостей. Владикавказ: СОГУ, 2009. – 475с.

68.  Долгарев А.И., Долгарев И.А. Некоторые приложения галилеевых методов. // Известия высших учебных заведений. Поволжский регион. Физико-математические науки, Пенза: ИИЦ ПГУ, 2009, № 2(9), с. 39 – 59.

  1. Connes A. Nonkommutative differential geometry.// Inst Hautes Etudes Sci. Publ. Math.,

     62(1985) – 257 – 360.

70.  Бахман Ф. Построение геометрии на основе понятия симметрии. – М.: Наука, 1969.             

      – 380с.

71. Долгарев А.И. Структура галилеева пространства-времени. – Materialy VIII Mezi-

      narodni vedecko-praktika conference “Aplikovane vedecke novinky 2012” 27 cervencu –

      05 srpna roku, DIL 12, Matematika, fyzika, moderni informacni technologie, vistavba a

      architektura. – Praha, Publishing House “Edukation and Science”  s.r.o. 2012. – p. 13 –

      21.

   72. Владимиров Ю.С. Пространство-время: явные и скрытые размерности. Изд.2 – М.:          

          Книжный дом «ЛИБРОКОМ», 2010. – 208с.

   73. Долгарев А.И. 2-параметрические кривизна и кручение 3-мерных галилеевых оду-

          лярных разрешимых пространств. – Известия высших учебных заведений.  По- 

         волжский  регион.  Физико-математически  науки, Пенза, 2007,  № 4, С. 3 – 17.