М. П. Ленюк
Чернівецький факультет НТУ”ХПІ”
Гібридне
інтегральне перетворення типу Лежандра-
-Фур’є -Ейлера на полярній осі r ≥R0 >0
Запровадимо методом
дельта-подібної послідовності інтегральне перетворення, породжене на множині
![]()
гібридним диференціальним оператором (ГДО)
![]() (1)
(1)
Тут ![]() –одинична функція Гевісайда [1],
–одинична функція Гевісайда [1], ![]() -узагальнений диференціальний оператор Лежандра [3],
-узагальнений диференціальний оператор Лежандра [3], ![]() -диференціальний оператор Ейлера другого порядку [2],
-диференціальний оператор Ейлера другого порядку [2], ![]() - диференціальний оператор Фур’є
другого порядку [2].
- диференціальний оператор Фур’є
другого порядку [2].![]()
Означення. Областю визначення ГДО M![]() назвемо множину G вектор-функцій
g(r)={g1 (r); g2 (r); g3 (r)} з такими властивостями:
назвемо множину G вектор-функцій
g(r)={g1 (r); g2 (r); g3 (r)} з такими властивостями:
1) вектор-функція ![]() ={
={![]() неперервна на
неперервна на ![]() ;
;
2) функції ![]() задовольняють крайові умови
задовольняють крайові умови
![]() ,
, ![]() , (2)
, (2)
3) функції ![]() задовольняють умови спряження
задовольняють умови спряження
![]() ,
, ![]() (3)
(3)
Умови та коефіцієнти: ![]()
![]()
Визначимо числа
![]()
вагову функцію
![]() (4)
(4)
та скалярний добуток
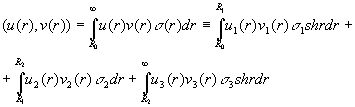 (5)
(5)
Нагадаємо, що з умов спряження
(3) випливає базова тотожність: для ![]() та
та ![]() має місце рівність
має місце рівність
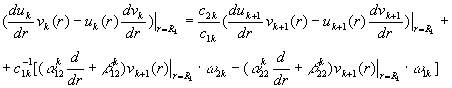 (6)
(6)
для випадку, коли умови спряження неоднорідні,
тобто
![]() (7)
(7)
Якщо
умови спряження однорідні ![]() , то в правій частині (6) відсутній другий доданок:
, то в правій частині (6) відсутній другий доданок:
![]() (8)
(8)
Методом
інтегрування два рази частинами під знаком інтегралів з послідуючим
використанням крайових умов (2), базової тотожності (8) та структури ![]() встановлюється
рівність
встановлюється
рівність
![]() (9)
(9)
Рівність
(9) показує, що ГДО ![]() -самоспряжений оператор. Отже, його спектр дійсний. Оскільки ГДО
-самоспряжений оператор. Отже, його спектр дійсний. Оскільки ГДО ![]() має на множині
має на множині ![]() одну особливу точку
одну особливу точку ![]()
![]() , то його спектр неперервний [4].
Можна вважати, що спектральний параметр
, то його спектр неперервний [4].
Можна вважати, що спектральний параметр ![]() . Йому відповідає дійсна спектральна вектор-функція
. Йому відповідає дійсна спектральна вектор-функція
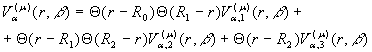 (10)
(10)
При цьому функції ![]() повинні задовольняти
відповідно диференціальні рівняння
повинні задовольняти
відповідно диференціальні рівняння
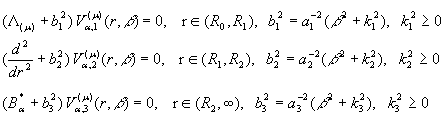 (11)
(11)
крайові умови (2) та умови спряження (3).
Фундаментальну систему розв’язків
для диференціального рівняння Лежандра ![]() складають функції
складають функції ![]() та
та ![]() [3];
фундаментальну систему розв’язків для диференціального рівняння Ейлера
[3];
фундаментальну систему розв’язків для диференціального рівняння Ейлера ![]() складають функції
складають функції ![]() та
та ![]() ; фундаментальну систему розв’язків для диференціального
рівняння Фур’є
; фундаментальну систему розв’язків для диференціального
рівняння Фур’є ![]() складають тригонометричні функції
складають тригонометричні функції
![]() та
та ![]() [2].
[2].
Якщо, скориставшись
фундаментальною системою розв’язків, покласти
![]()
![]() (12)
(12)
![]()
то крайова
умова в точці ![]() та умови спряження (3) для
визначення шести величин
та умови спряження (3) для
визначення шести величин ![]() дають однорідну
алгебраїчну системи з п’яти рівнянь:
дають однорідну
алгебраїчну системи з п’яти рівнянь:
![]()
![]()
![]() (13)
(13)
В алгебраїчній системі (13)
беруть участь функції
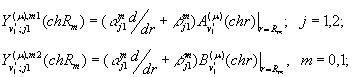
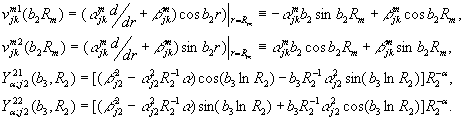
Алгебраїчна система (13) сумісна.
Побудуємо її розв’язок стандартним способом [5].
Нехай ![]() ,
, ![]() , де
, де ![]() підлягає визначенню. Перше рівняння системи (13) стає
тотожністю. Для визначення величин
підлягає визначенню. Перше рівняння системи (13) стає
тотожністю. Для визначення величин ![]() отримуємо алгебраїчну систему:
отримуємо алгебраїчну систему:
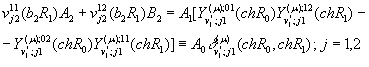 (14)
(14)
Визначник алгебраїчної системи (14) обчислюється
безпосередньо:
![]()
Алгебраїчна система (14) має
єдиний розв’язок [5]:
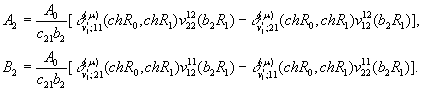 (15)
(15)
При відомих ![]() для визначення
для визначення ![]() одержуємо алгебраїчну систему з
двох рівнянь:
одержуємо алгебраїчну систему з
двох рівнянь:
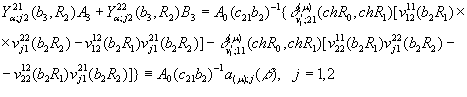 (16)
(16)
Визначник алгебраїчної системи обчислюється безпосередньо:
![]()
Алгебраїчна система (16) має
єдиний розв’язок [5]:
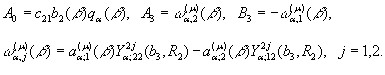 (17)
(17)
Підставивши визначені за
формулами (15) та (17) величини ![]() у рівності (12),
отримуємо функції:
у рівності (12),
отримуємо функції:
![]()
![]()
![]()
![]() (18)
(18)
Згідно формули (10) спектральна вектор-функція ![]() стає відомою (визначена).
стає відомою (визначена).
Наявність вагової функції ![]() , спектральної вектор-функції
, спектральної вектор-функції ![]() та спектральної щільності
та спектральної щільності
![]()
![]()
дає можливість визначити пряме ![]() та обернене
та обернене ![]() гібридне інтегральне перетворення
(ГІП), породжене на множині
гібридне інтегральне перетворення
(ГІП), породжене на множині ![]() ГДО
ГДО ![]() [6,7]:
[6,7]:
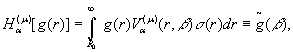 (19)
(19)
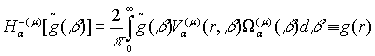 (20)
(20)
Математичним обґрунтуванням
правил (19), (20) виступає твердження.
Теорема
1 (про
інтегральне зображення). Якщо вектор-функція
![]()
неперервна, абсолютно сумовна й має обмежену
варіацію на множині ![]() , то для будь-якого
, то для будь-якого ![]() справджується
інтегральне зображення:
справджується
інтегральне зображення:
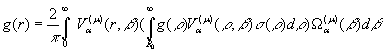 (21)
(21)
Доведення: В основі доведення
теореми знаходиться подвійний невласний інтеграл
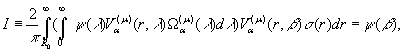 (22)
(22)
якщо ![]() , і дорівнює нулю, якщо
, і дорівнює нулю, якщо ![]() .
.
Формула (22) встановлюється
методом дельта-подібної послідовності (ядро Діріхле).
Припустимо, що функція
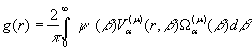 (23)
(23)
Помножимо рівність (23) на вираз ![]() та проінтегруємо по
та проінтегруємо по ![]() від
від ![]() до
до ![]() . Внаслідок рівності (22) будемо мати:
. Внаслідок рівності (22) будемо мати:
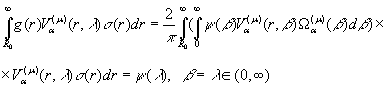 (24)
(24)
Якщо тепер підставити в (23)
згідно рівності (24) функцію
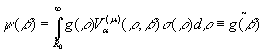
то одержуємо інтегральне
зображення (21).
Доведення
теореми завершено.
Зауваження. Якщо функція ![]() кусково-неперервна,
то ліву частину в (21) треба замінити на
кусково-неперервна,
то ліву частину в (21) треба замінити на ![]()
Введемо до розгляду
величини та функції:
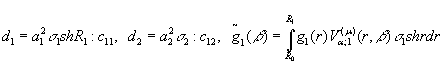
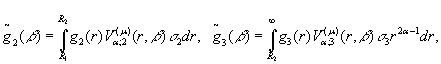
![]()
Теорема
2
(про основну тотожність). Якщо
вектор-функція
![]() неперервна на множині
неперервна на множині
![]() , а функції
, а функції ![]() задовольняють крайові
умови
задовольняють крайові
умови
![]() (25)
(25)
та умови спряження
![]() (26)
(26)
то має місце основна тотожність ГІП ГДО ![]() :
:
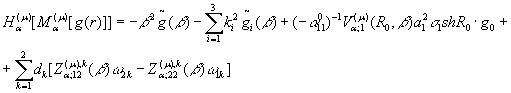 (27)
(27)
Доведення проводиться за логічною
схемою доведення ідентичних теорем
[6,7].
Одержані правила (19, (20) та
(27) складають достатньо ефективний математичний апарат для одержання
інтегрального зображення точного аналітичного розв’язку алгоритмічного
характеру широкого класу стаціонарних і нестаціонарних задач математичної
фізики неоднорідного середовища. Крім цього, дане інтегральне перетворення
можна використати для обчислення невласного інтегралу за власними елементами
ГДО ![]() , визначеного рівністю (1).
, визначеного рівністю (1).
Зауважимо, що без залучення нових
ідей, можна поширити гібридні інтегральні перетворення на будь-яку скінченну
кількість точок спряження в будь-якій комбінації (в будь-якому сполученні)
диференціальних операторів Фур’є, Ейлера та Лежандра.
Література:
1. Шилов Г.Е. Математический
анализ. Второй специальний курс. – М.: Наука, 1965. –
328с.
2. Степанов В.В. Курс дифференциальних уравнений. – М.: Физматгиз, 1959. – 468с.
3. Конет І.М., Ленюк М.П.
Інтегральні перетворення типу
Мелера-Фока. – Чернівці: Прут, 2002. – 248с.
4. Ленюк М.П., Шинкарик М.І.
Гібридні інтегральні перетворення (Фур’є, Бесселя, Лежандра). Частина 1. –
Тернопіль: Економічна думка,
2004. – 348с.
5. Курош А.Г. Курс высшей алгебры.
– М.: Наука, 1971. – 432с.
6. Ленюк М.П. Гібридні інтегральні
перетворення типу Ейлера-(Фур’є, Бесселя). – Львів, 2009. – 76с.-(Препринт/ НАН
України. Інститут прикл. проблем механ. і матем. ім. Я.С. Підстригача; 02.09).
Чернівці: Прут, 2009.
7. Ленюк М.П., Шинкарик М.І.
Гібридні інтегральні перетворення (Фур’є, Ейлера, Бесселя, Лежандра). Частина
2. – Тернопіль: Економічна думка, 2011. – 384с.