12rusnauka11

к.ф.-м.н. И.А. Долгарев, к.ф.-м.н. А.И. Долгарев

НЕОДНОРОДНСТЬ ПРОСТРАНСТВЕННОЙ СОСТАВЛЯЮЩЕЙ

ПРОСТРАНСТВА-ВРЕМЕНИ

В работе указаны некоторые неоднородные пространства. Установлено, что неоднородны 3-мерные евклидовы подпространства псевдоевклидова и галилеева пространства-времени.

Неоднородность псевдоевклидова пространства-времени тривиальна. Если псевдоевклидово пространство размерности 4 индекса 1, то его временная составляющая 1-мерна, пространственная составляющая 3-мерна и евклидова. Не существует движений пространства-времени, в которых временное направление заменялось бы пространственным и движений с обратным свойством. Это и есть очевидное свойство неоднородности пространства-времени. Пространство обладает и другими свойствами неоднородности. Упомянутые свойства подробно обоснованы П.К. Рашевским в [1], однако П.К. Рашевский изучает свойства псевдоевклидовых движений, их структуру, и не останавливается на попутно полученной неоднородности пространства-времени. Временная составляющая пространства-времени неинвариантна в движениях пространства-времени. Пространственная составляющая неоднородна, хотя и является 3-мерным евклидовым пространством. Ниже в результатах П.К. Рашевского выделена неоднородность евклидовой составляющей псевдоевклидова пространства-времени.

Пространство-время Галилея является предельным случаем псевдоевклидова пространства-времени при условии, что скорости событий малы по сравнению со скоростью света. Поэтому и пространственная составляющая пространства Галилея неоднородна.

В работе указаны некоторые неоднородные пространства (аффинные, евклидовы). Выявлена неоднородность 3-мерных евклидовых подпространств псевдоевклидова и галилеева пространства-времени.

1. Аффинные геометрии

1.1. Однородная аффинная геометрия

Пусть есть действительное линейное пространство аффинного пространства , в котором выбран репер = . Базисом линейного пространства является = . Определяя в скалярное произведение векторов, превращаем аффинное пространство в одно из евклидовых пространств. Аффинные преобразования и движения евклидовых пространств изучаются в [1]. Эти преобразования можно задать указав, на какой репер отображается репер . Выбор репера на свойствах преобразований не отражается. Если в репере : , = = , , то матрица преобразования имеет вид:

, , .

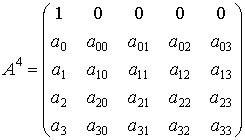Репер может быть произвольным. В этом состоит свойство однородности аффинного пространства. Аффинные преобразования пространства составляют группу. Согласно Эрлангенской программе Ф. Клейна, аффинная геометрия изучает инварианты группы аффинных преобразований.

1.2. Неоднородные аффинные геометрии

В аффинной геометрии можно выделять и неоднородные теории. Можно, например, рассматривать аффинные преобразования пространства , в которых направление инвариантно ( есть линейная оболочка вектора ). Это означает, что векторы из отображаются на векторы из и на векторы из никакие другие векторы из не отображаются, кроме векторов из . Матрицы указанных преобразований:

, , , .

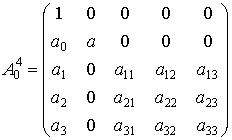При этом оказывается, что и 3-мерное направление инвариантно в преобразованиях с матрицами .

Преобразования рассматриваемого вида составляют группу, обозначим ее . Говорим, что группа стабилизирует направление и стабилизирует направление . В геометрии, изучающей инварианты группы преобразований , направление (и направление ) инвариантно, это направление не отображается преобразованиями группы ни на какое другое 1-мерное направление в пространстве . Таким образом, аффинная геометрия, изучающая инварианты группы , неоднородна.

Нетрудно указать и другие виды неоднородных аффинных геометрий. Например, геометрия пространства, в котором стабилизируется направление , оно стабилизируется преобразованиями с матрицами вида

, , .

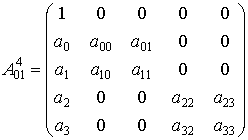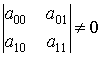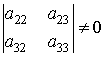2. Евклидовы геометрии

2.1. Однородная евклидова геометрия

В линейном пространстве аффинного пространства может быть введено собственноевклидово скалярное произведение векторов. Пусть в базисе = заданы векторы и . Их скалярным произведением называется число

.

Это скалярное произведение называется собственноевклидовым. Скалярный квадрат вектора равен

;

норма вектора определяется из и вычисляется по формуле

.

В результате линейное пространство становится собственно евклидовым и обозначается = . Аффинное пространство превращается в евклидово пространство .

Свойства евклидова векторного пространства можно найти, например, в [2]. Заметим, что в общем случае скалярное произведение векторов задается матрицей Грама.

Движения евклидова пространства задаются галилеевой матрицей вида из п. 1.1 с условием . При этом всякое направление , , т.е. 1-мерное подпространство пространства , отображается в его движениях на всякое направление пространства . Указанное свойство пространства является свойством его однородности.

2.2. Неоднородные евклидовы геометрии

Движения евклидова пространства с матрицами вида из п. 1.2 с условием ведут к неоднородному евклидову пространству. Его геометрия определяется группой движений (смысл обозначения в п. 1.2).

Движения евклидова пространства с матрицами вида и условием

,

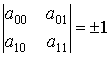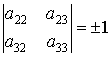
определяют неоднородную евклидову геометрию с другими свойствами.

3. Псевдоевклидово пространство

3.1. Псевдоевклидово пространство индекса 1

В базисе линейного пространства определено следующее псевдоевклидово скалярное произведение векторов и :

.

Линейное пространство становится псевдоевклидовым индекса 1 векторным пространством , аффинное пространство превращается в псевдоевклидово пространство индекса 1, обозначаемое . Псевдоевклидов скалярный квадрат вектора равен

.

Для векторов базиса выполняются равенства: , , . Репер является ортонормированным. Для вектора компонента называется временной, компоненты называются пространственными. Пространственная составляющая пространства-времени состоит из событий и является 3-мерным собственноевклидовым пространством . Всякое событие пространства-времени содержится в единственной евклидовой гиперплоскости , содержащей только одновременные события .

Любой вектор , , является временным. Имеем сумму = , где =, но это не инвариантная в движениях сумма. Как выяснится ниже, п. 3.3, теорема 4, тоже не инвариантная в псевдоевклидовых движениях сумма подпространств.

3.2. Движения псевдоевклидова пространства

Движением псевдоевклидова пространства является его аффинное преобразование, в котором инвариантно псевдоевклидово скалярное произведение векторов. Множество всех псевдоевклидовых движений является группой относительно композиции преобразований. Движение пространства-времени задается двумя реперами . Репер может быть зафиксирован. Поэтому о движении (и об аффинном преобразовании) можно говорить как о преобразовании репера в репер (последний термин используется в [1]).

Обозначим движение пространства через , считаем, что есть преобразование репера в репер , можно считать . Пусть в гиперплоскость = отображается на гиперплоскость =. Если = , то есть «тривиальное» евклидово вращение (как пишет П.К. Рашевский). В этом случае . Если , то пересечение 2-мерно, имеем = , [1, c. 200]. С точностью до «тривиальных» вращений плоскости , выполняются равенства

, . (1)

(В [1] это соотношения (48.10), с. 200). Эти «тривиальные» вращения плоскости описываются равенствами:

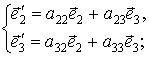
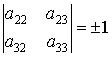. (2)

Плоскости , совпадают, [1, c.200], поэтому, в движении псевдоевклидовой плоскости,

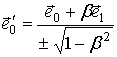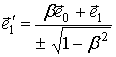, . (3)

Это соотношения (48.11) в [1, c.200]. В завершение описания движения из [1, c. 198 – 201] приведем цитату.

«В результате всякое преобразование ортонормированного репера с точностью до тривиальных вращений и параллельного сдвига сводится к преобразованию (48.10), (48.11).» У нас это (1) и (3).

С точностью до (2) и (3) матрица движения есть , где

, , , ,

.

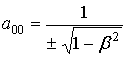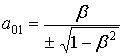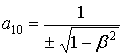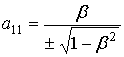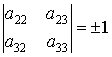Выписанная матрица охватывает матрицы параллельных сдвигов и матрицы всех тривиальных вращений евклидовых пространств и .

3.3. Неоднородность пространственной составляющей

Приведенная выше цитата из [1, c.201] есть невыделенная в тексте книги основная теорема П.К. Рашевского о движениях псевдоеклидова пространства . Этим описывается и неоднородность пространственной составляющей пространства , на что указывает матрица преобразования .

Вместе с основной теоремой П.К. Рашевского о движениях псевдоевклидова пространства, справедливы следующие утверждения, тоже не приведенные в [1].

Теорема 1. Евклидова плоскость , как пересечение евклидовых гиперплоскостей = и =, инвариантна в псевдоевклидовых движениях.

# Можно предположить, что исходный репер не содержит векторов , а содержит . Имеем репер = в качестве исходного. Рассматриваем преобразование репера в репер . При этом получаем, как в [1, c. 200], пересечение подпространств и (или после параллельного переноса , пересечение гиперплоскостей и ). Это пересечение, по основной теореме Рашевского, является плоскостью . В преобразовании репера в репер пересечение есть .

Инвариантное направление в единственно. Оно стабилизируется группой движений, матрицы которых есть . #

Приходится говорить о 3-мерном евклидовом направлении пространственной составляющей пространства-времени ; через каждую точку пространства-времени проходит единственная евклидова гиперплоскость с векторным пространством . При движении точки в пространстве гиперплоскость движется параллельно сама себе.

Теорема 2. Движения псевдоевклидова пространства-времени стабилизируют 2-мерное направление пространственной составляющей пространства-времени .

# Матрицы движений пространства-времени содержат ненулевые блоки

= , =

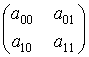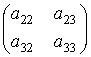
с ненулевыми определителями и блоки

, ,

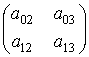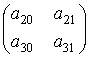состоящие из нулей. Таким образом, направление в стабили-зируется движениями пространства . Стабилизируется это направление и в подпространстве =. #

Теорема 3. Псевдоевклидово пространство-время является прямой суммой псевдоевклидовой плоскости и евклидовой плоскости; эти подпространства инвариантны в псевдоевклидовых движениях.

# Движения пространства отображают каждое из 2-мерных направлений , само в себя. #

Вместе с тем выполняется

Теорема 4. 1-мерная временная составляющая пространства не инвариантна в псевдоевклидовых движениях, т.е. разложение пространства-времени на временную и пространственную составляющие не инвариантно в псевдоевклидовых движениях.

# По виду матриц псевдоевклидовых движений, движения пространства-времени не стабилизируют направления . #

Как алгебраическая структура, векторное пространство есть прямая сумма +. Но эта прямая сумма не инвариантна в автоморфизмах структуры , в которых инвариантно псевдоевклидово скалярное произведение векторов.

Утверждения настоящего п. 3.3 являются уточнениями основной теоремы П.К. Рашевского о движениях псевдоевклидова пространства .

4. Пространство-время Галилея

4.1. Геометрия Галилея

В линейном пространстве аффинного пространства определим галилеево скалярное произведение векторов. Для векторов и полагаем по определению:

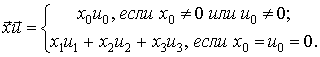
Линейное пространство превращается в галилеево векторное пространство , аффинное пространство становится пространством Галилея . Галилеево скалярное произведение векторов определено в [3], оно определено не одним равенством, как евклидово и псевдоевклидово скалярные произведения векторов, а двумя равенствами. Такое скалярное произведение векторов, согласно Б.А. Розенфельду, относится к квазискалярным произведениям, (в [4, c. 41] говориться о квазинормах, квазискалярные произведения не рассматриваются.) Галилеева норма векторов, т.е. квазинорма, такова:

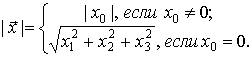
Определение галилеева расстояния между точками можно найти в математической энциклопедии.

По аналогии с терминологией в псевдоевклидовой геометрии вводится галилеева терминология. Векторы , , называются временными, векторы называются евклидовыми или пространственными. есть пространство-время. Точки из называются еще событиями. Для значения имеется множество событий , одновременных с событием ; это множество событий представляет собой 3-мерное евклидово пространство – подпространство пространства-времени Галилея . В каждый фиксированный момент времени имеется пространственная составляющая пространства-времени .

4.2. Преобразования Галилея

Геометрической основой принципа относительности А. Эйнштейна является псевдоевклидова геометрия, а геометрической основой принципа относительности Галилея является геометрия Галилея. Фундаментальное рассмотрение вопросов псевдоевклидовой геометрии имеется в книге [1]. 3-мерная геометрия Галилея изложена в [3], некоторые вопросы 4-мерной геометрии Галилея содержатся в [5] и других работах авторов. Преобразования Лоренца, т.е. движения псевдоевклидова пространства, анализируются в [1]. Формулы Лоренца:

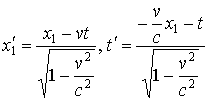, . (4)

В (3) . При малых значениях скоростей по сравнению со скоростью света , величина . А в этом случае Лоренцева механика заменяется классической механикой Галилея-Ньютона. Геометрия Галилея является предельным случаем псевдоевклидовой геометрии. При малых скоростях по сравнению со скоростью света движений материальных объектов формулы (4) превращаются в формулы Галилея:

, . (5)

4.3. Пространственная составляющая пространства-времени Галилея

Событие пространства-времени Галилея имеет временную составляющую и пространственную составляющую . В фиксированный момент времени множество всех событий есть евклидово пространство . В движениях пространства-времени , см. (5), компоненты и связаны между собой, компоненты не зависят от изменения компонент и .

Пространство-время имеет своим векторным пространством = с галилеевым скалярным произведением векторов. Согласно (5) выделяются направления = и = , первое из них галилеево, второе собственно евклидово. В указанные направления определяют пучки параллельных плоскостей: плоскостей Галилея с векторным пространством и евклидовых плоскостей с векторным пространством . Таким образом, справедлива

Теорема 5. Пространственная составляющая пространства-времени Галилея неоднородна. Пространство-время Галилея является прямой суммой плоскости Галилея и евклидовой плоскости

= .

Указанные прямые слагаемые инвариантны в галилеевых преобразованиях.

4.4. Следствия неоднородности пространственной составляющей

По теореме 5, основанной на формулах Галилея (5), пространственная составляющая пространства-времени Галилея является множеством событий вида , обладает 2-мерным инвариантным в галилеевых преобразованиях направлением ; в указанном множестве событий это подмножество событий вида . Формулы преобразований Галилея (5) характеризуют подвижность пространства-времени Галилея. Подвижность ограничена ввиду неоднородности пространства-времени.

Неоднородность пространства-времени состоит в том, что

во-первых: преобразованиями Галилея временное направление отображается только на временное направление и не отображается ни на какое пространственное направление и никакое пространственное направление в пространстве-времени Галилея не отображается на временное направление;

во-вторых: в пространстве Галилея галилеева плоскость , имеющая направление , отображается только на галилееву плоскость с направлением (возможны галилеевы плоскости с различными направлениями, например, еще ), евклидова плоскость отображается на евклидову плоскость , т.е. направление отображается на направление ;

в-третьих: существует единственное пространственное направление , инвариантное в преобразованиях Галилея, что означает справедливость следующего утверждения.

6. Теорема. Всякая подвижная система отсчета в пространстве-времени Галилея движется только в инвариантном направлении .

В этом состоит подвижность (ограничение подвижности) пространства-времени Галилея.

4.5. Следствия увеличения подвижности

Если предположить пространство-время Галилея более подвижным, то это влечет и изменение неоднородности пространства-времени. Согласно теореме 6, вектор скорости движения подвижной системы отсчета коллинеарен инвариантному направлению пространства-времени и может быть записан в виде . Система отсчета движется в случае .

В статье А.З. Петрова в математической энциклопедии приведены следующие формулы галилеева преобразования (с точностью до обозначений):

, , , , (6)

[6, c. 844]. Здесь есть вектор скорости движения подвижной системы отсчета относительно неподвижной. Формулы Петрова (6) отличаются от общепринятых формул (5) в двух последних компонентах. Согласно п. 2.2, в общем случае компоненты и могут быть связаны на основе формул (2), но через временную компоненту они не выражаются. Похоже, что формулы (6) написаны в предположении однородности пространственной составляющей пространства-времени Галилея.

Покажем противоречивость формул (6).

7. Теорема. Из формул Петрова (6) следует противоречивость пространства-времени Галилея.

# Из последнего равенства в (6):

.

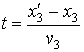Подставляя это значение во все равенства в (6), находим:

.

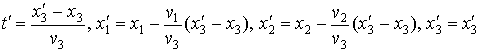Последняя компонента не изменяется, что естественно. Временная компонента оказалась выраженной только через пространственные компоненты, что невозможно. Таким образом, в формулах преобразований Галилея должно быть не более одной пространственной компоненты, которая выражается через временную компоненту, см. (5). #

Итак, помимо тривиальной неоднородности пространства-времени в результате изучения допустимых преобразований пространства-времени выявляется ограничение подвижности и, более того, неоднородность евклидовой составляющей пространства-времени как пространств СТО и ОТО, так и пространства Галилея. Подвижность евклидова пространства, рассматриваемого независимо, отличается от его подвижности, если оно включено в другое пространство с некоторой спецификой, в частности, если оно является частью пространства-времени.

Использованная литература

1. Рашевский П.К. Риманова геометрия и тензорный анализ. - М.: Наука, 1967. - 664с.

2. Кострикин А.И., Манин Ю.И. Линейная алгебра и геометрия,- 2-ое изд.,

перераб. - М.: Наука, 1986, - 304 с.

3. Долгарев А.И. Классические методы в дифференциальной геометрии одулярных пространств. Монография. – Пенза: ИИЦ ПГУ, 2005.- 306с.

4. Розенфельд Б.А., Замаховский М.П. Геометрия групп Ли. Симметрические, параболические и периодические пространства. – М.: МЦНМО, 2003. - 560с.

5. Долгарев А.И., Долгарев И.А. Кривые 4-мерного пространства-времени Галилея. // Известия высших учебных заведений. Поволжский регион. Физико-математические науки, Пенза: ИИЦ ПГУ, 2007, № 3, с. 2 – 11.

6. Математическая энциклопедия. Т. 1. – М.: Советская энциклопедия, 1977. – 1152 с.