Экономические науки/ 8.Математические методы в экономике

Снежкина О.В., Левова Г.А.

Пензенский государственный университет архитектуры и строительства, Россия

Прогнозирование экономических показателей

с помощью временных рядов

Среди математических методов прогнозирования в особую группу выделяются методы экстраполяции, которые отличаются простотой, наглядностью и легко реализуются на ЭВМ. Методологическая предпосылка экстраполяции состоит в признании преимущественной связи между прошлым, настоящим и будущим. При этом развитие экономических явлений наиболее полно находит свое отражение во временных рядах, которые представляют собой упорядоченные во времени наборы измерений каких-либо характеристик исследуемого объекта, процесса. В настоящее время разработана большая группа экстраполяционных методов прогнозирования отдельных экономических показателей.

Наиболее распространенными методами оценки параметров аппроксимирующих зависимостей являются метод наименьших квадратов (МНК) и его модификации, метод экспоненциального сглаживания, метод вероятностного моделирования, метод адаптивного сглаживания.

Метод наименьших квадратов состоит в определении параметров модели тренда, минимизирующих ее отклонение от точек исходного временного ряда:

Рассмотрим практические стороны построения точечных и интервальных прогнозов на основе анализа временных рядов на примере ежеквартальных данных с 2007 года по настоящее время о стоимости газа в многоквартирных домах города Пензы .

Для получения прогноза о стоимости газа необходимо получить модель временного ряда. Анализ временного ряда начинают с построения и изучения его диаграммы (рис. 1).

Визуальный анализ диаграммы данного ряда позволяет уверенно сказать, что временной ряд имеет тенденцию и не имеет сезонных и циклических компонент. Предположим, что характер тренда линейный. Определим модель тренда методом наименьших квадратов как

y(t)=a+bt.

Полученная модель тренда

y(t)=17,64+1,27t

имеет очень высокие показатели адекватности:

· коэффициент детерминации R²=0,917, таким образом, полученная модель на 92% объясняет изменение стоимости;

· уровень значимости F-критерия составляет 6,84E-08, что существенно меньше 0,01, т.е. полученная модель является высоко значимой;

· уровень значимости t-критерия составляет 2,55E-10, что существенно меньше 0,01, следовательно, все коэффициенты статически значимы.

В целом можно сделать вывод, что полученная модель тренда достаточно адекватно описывает исследуемую статистическую зависимость и вполне пригодна для получения обоснованных заключений и прогнозов.

Экономическая интерпретация модели позволяет сделать вывод о том, что цена на газ в г. Пенза за квартал дорожает в среднем на 1 рубль 27 копеек.

Рассмотрим процесс получения интервальных прогнозов по формуле

,

Где - точечный прогноз;

-критическое значение t- критерия при уровне значимости α и числе степеней свободы m=n-2 (t_0,05;12= 2,2);

-ошибка прогноза.

Ошибку прогноза определяется по формуле:

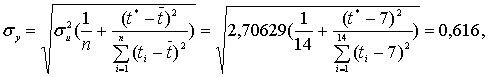
- дисперсия отклонений;

t*- порядковый номер периода времени, на который рассчитывается прогноз.

Очевидно, что использование полученной модели тренда для среднесрочного и тем более долгосрочного прогнозирования недопустимо.

Предвидя возможные возражения относительно корректности практического использования полученных прогнозов, необходимо отметить, что определенная условность всегда присуща выводам, получаемым на основании прогнозирования. Это связано с тем, что целый ряд статистических методов базируется на довольно жестких требованиях к качеству обрабатываемых данных (например, к их однородности) и строгих гипотезах о характере поведения анализируемых величин (их распределениях). Таким образом, для практика остаются две альтернативы: или вообще отказаться от применения большинства методов и довольствоваться достаточно скудным и примитивным инструментарием, или применять разнообразные статистические методы обработки данных, не забывая о соответствующих этим методам требованиям.

Рис.1