Физика/2. физика твердого тела

Вазанков Д.Б., Грозенко М.О.

 

Автомобільно-дорожній інститут Донецького Національного Технічного Університету, Україна

 

Дифузійно – дислокаційний механізм як основа низькотемпературної пластичної деформації алмазоподібних кристалів

Припущення того, що трансляційна симетрія кристалу диктує періодичний характер залежності сил опору гратки зсувній та пружній деформації, покладене  Я.І. Френкелем в основу розрахунку теоретичної міцності кристалу. Велике розходження знайдених теоретично та експериментально значень  стало вирішальним стимулом  у виникненні дислокаційної гіпотези того, що рух дислокації може відбуватись і при відносно низьких напруженнях.

Для вирішення вказаного питання фізики пружності та міцності було створено ряд моделей. Найбільший розвиток отримала модель Пайєрлса, в якій враховано дальнодіючі сили, що виникають при зсуві двох частин кристалу вздовж площини ковзання, в якій дотичні напруження нелінійно залежать від різниці тангенційних зміщень атомів, що знаходяться по різні сторони від площини ковзання. Мінімальне напруження  (напруження Пайєрлса), необхідне для руху дислокацій в потенційному полі кристалічної гратки (рис.1, а) в цьому випадку виявляється набагато більшим ніж розраховане експериментально. Тому була висунута ідея про можливість руху дислокацій при напруженнях, менших ніж , за рахунок поступового подолання пайєрлсовського рельєфу при зародженні пар перегинів та їх розходження вздовж діслокаційної лінії (рис. 1).

 

Припускається, що залежність сил опору кристалу для руху дислокації має період, що дорівнює мінімальній відстані між  рядами атомів, паралельних лінії дислокації. Найчастіше приймається синусоїдальний вид функції, що описує зміну енергії дислокації  від її  координати x в площині ковзання. В найпростішому випадку для крайової дислокації

 

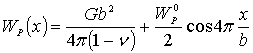                        ,                          (1)

 

 

де G – модуль зсуву,  - коефіцієнт Пуассона, -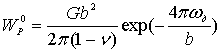

енергія Пайєрлса, 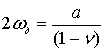 – відстань, на якій зсув атомів з положення рівноваги  на площині ковзання при утворенні дислокації дорівнює , тобто половині зсуву на нескінченності, a  - відстань між сусідніми атомами, що паралельні площині ковзання, b – вектор Бюргерса. Класичний рух всієї дислокації як цілого з однієї канавки потенціального рельєфу можливий  лише при напруженнях , що перевищують напруження Пайєрлса.

 

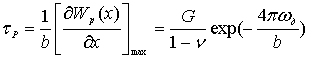                       (2)

 

Дані по оцінці швидкості руху  дислокацій в Si, Ge (Альохін)  на стадіях мікротекучості  та мікродеформації свідчать про аномалію пластичного руху поблизу вільної поверхні кристалу і про більш високу швидкість руху дислокацій в його при поверхневих шарах.   Розраховані значення швидкостей руху дислокацій у при поверхневих шарах Si в інтервалі температур 680о – 900о С виявились на 1 – 1,5 порядків вище відповідних значень швидкостей руху дислокацій, відомих з літературних даних для об’ємної пластичної течії, де розмір дислокаційних напівпетель більше ніж 300 мкм. Наприклад, згідно отриманим даним, при Т = 700оС, , , в той час як теоретично розрахована швидкість руху одиночних дислокаційних напівпетель складає .

Підвищення рухливості дислокацій при Т = 300 К обумовлено, насамперед, сприятливою можливістю їхнього неконсервативного руху, оскільки поверхня є практично нескінченним джерелом і стоком точкових дефектів. Слід, також, відзначити підвищену рухливість при поверхневих дислокацій, обумовлену впливом сил зображення і дією фактора переповзання. Найбільш рухливими місцями дислокаційних ліній є їхні при поверхневі ділянки в шарі товщиною до 100 мкм. При цьому роль сил зображення і вільної поверхні полягає не тільки в посиленні тенденції до неконсервативного руху, але й у збільшенні ефективної напруги з  і, як наслідок цього, у збільшенні швидкості дислокацій V() .

У моделі Пайєрлса - Набарро енергія дислокації періодично залежить від положення її центра, а опір гратки відповідає максимальному дотичному напруженню  (напруга Пайєрлса). Для подолання потенційного бар'єру на одиницю довжини дислокації повинна діяти сила  (b — вектор Бюргерса). В монографії В.П. Альохіна приведені такі значення напруги Пайєрлса:  = 210 кгс/мм2 для Ge і = 270 кгс/мм2 для  Si. Оскільки в реальних кристалах дислокації можуть рухатись при напругах  < , вважається, що вони можуть долати бар'єр Пайєрлса за допомогою термофлуктуаційного утворення подвійного перегину і бічного поширення перегинів уздовж дислокації (рис.1). При цьому швидкість руху всієї дислокації  визначається лінійною густиною перегинів п, швидкістю їхнього переміщення n і відстанню між сусідніми канавками потенційного рельєфу а :  = a nn. Імовірність зародження перегинів залежить від Т та . Однак не всякий зароджений подвійний перегин здатний розширюватися при даному рівні прикладених напружень; якщо відстань між парними перегинами менше критичної, то перегин може захлопнутися.

До цього часу детально розроблено кілька моделей зародження і руху подвійного перегину: модель дислокаційної струни ; модель дифузійного доростання перегинів ; модель, що враховує вплив крапкових дефектів як точок гальмування на швидкість руху дислокацій , а також, модель переміщення дислокації зі сходинками .

У зв’язку з тим, що швидкість дислокації різко збільшується при виході її на вільну поверхню кристалу, вираз для деякої ефективної енергії активації має наступний вигляд

 

,

 

де - енергія утворення поодинокого перегину біля поверхні зразку,  - енергія утворення подвійного перегину на дислокаційному сегменті;  - енергія утворення зміненого подвійного перегину;  - вклад в енергію активації руху дислокації, зв’язаний з наявністю в кристалі дефектів.

Вираз для енергії утворення подвійного перегину   в потенційному рельєфі  має вигляд

 

                                                   (3)

де - лінійна енергія дислокації;  x0  - положення стійкої рівноваги дислокації, що задовольняє умові .

Вираз для енергії утворення одиночного перегину для синусоїдальної форми рельєфу має вигляд

                                                                                  (4)

 

Модель дислокаційної струни застосована при досить великих , коли b3 > kТ. Для випадку малих  потрібно використовувати іншу модель. Відповідно до цієї моделі, під дією малих  дислокація лише злегка піднімається з  дна потенційного рельєфу. При дотриманні умови U0 > kТ  і   b3 >> kТ дислокація з подвійним перегином вважається складеною з відрізків, що встигають прийти в рівновагу з середовищем, і перехід дислокації в сусідню долину являє собою повільний дифузійний процес. Доростання подвійного перегину, утвореного термічною флуктуацією, до критичного розміру, відбувається в результаті дрейфу під дією різниці сил лінійного натягу, обумовленого перебуванням відрізків дислокації в різних долинах рел’єфу.

Існує теорія руху дислокацій у кристалах з великим бар'єром Пайєрлса, що враховує дію крапок гальмування на поширення перегинів уздовж лінії дислокації. При цьому передбачається, що навіть подвійний перегин, що перевершує критичний розмір, розширення якого зупинене бар'єрами крапок гальмування, має імовірність захлопнутися. Такими дефектами можуть бути вакансії, що переміщуються разом з дислокаціями, і комплекси вакансій.

 Аналіз існуючих моделей руху дислокацій у кристалах з високим бар'єром Пайєрлса показує, що в даний час немає загальної теорії, що описує з одних позицій динамічне поводження дислокацій у цих кристалах. Зіставлення теорії з експериментом дає кращу збіжність результатів у випадку використання в теоретичній моделі не подвійного, а поодинокого перегину. Можна  припустити, що найбільш імовірним джерелом утворення поодинокого перегину є вільна поверхня кристалу.

Переважна участь поодинокого перегину в динаміці руху дислокацій була підтверджена рядом робіт, експериментальні дані яких добре пояснювались   з позицій термічно активованого зародження в поверхні поодинокого перегину, як основного процесу, що контролює кінетику мікропластичної деформації.

Можна  відзначити, що роль поверхні як джерела полегшеного утворення перегинів, очевидно, дуже значна й особливо на початковій стадії деформації. Це збільшується ще тією обставиною, що, по-перше, величина і форма бар'єра Пайєрлса в приповерхневих шарах істотно відрізняються від аналогічних параметрів в об’ємі кристалу в силу специфіки атомно-електронної структури поверхні ; по-друге, імовірність термічної флуктуації і зародження перегину біля вільної поверхні набагато вище, тому що, середньоквадратичні зміщення атомів поблизу поверхні істотно вищі (), а температури Дебая істотно нижчі, ніж у внутрішніх шарах кристалу. Так, згідно експериментальним і розрахунковим даним, максимальна глибина аномалії по U2 складає приблизно 5  моношарів, тобто порядку 30 Ао для Si і Ge. Це дозволяє поодинокому чи подвійному перегину з  цілком зароджуватися в області з більш високим значенням U2 і низьким значенням величини бар'єра Пайєрлса відповідно.

З іншого боку, специфіка впливу поверхні на динаміку руху дислокацій виявляється також у зв'язку з тією обставиною, що рух дислокацій дуже часто відбувається змішаним шляхом, тобто об’єднанням консервативного руху з неконсервативним. Найчастіше процес ковзання і переповзання може спостерігатися на кінцях дислокаційних напівпетель, що виходять на вільну поверхню, оскільки тут йому допомагають дія сил зображення і дія самої поверхні як нескінченного джерела і стоку крапкових дефектів.

Таким чином, на підставі сказаного, запропонована дифузійно-дислокаційна модель руху дислокаційних петель, що об’єднує подвійне поперечне ковзання гвинтових сегментів, що обходять мікроскопічні перешкоди, і переповзання 60-градусних сегментів.

Відповідно до цієї моделі, динамічні характеристики руху дислокацій обумовлені дифузійним механізмом, по якому рух дислокацій визначається швидкістю переміщення сходинок, що генерують і поглинають із кристалу крапкові дефекти.

Природньо, що з викладених позицій постає зрозумілим вплив поверхні на швидкість руху дислокацій, що відіграє роль практично нескінченного джерела і стоку вакансій. При цьому дія поверхні зводиться до прискореного переміщення сходинок у результаті дифузії крапкових дефектів, що полегшує рух перегинів . Тому, як тільки дислокаційна петля виходить своїми кінцями на поверхню, її рух уже не лімітується обміном вакансій між 60-градусними компонентами петлі для переміщення наявних на них сходинок, а визначається в основному кінетикою обміну крапковими дефектами дислокації з поверхнею.

ЛІТЕРАТУРА:

1.            Swarezentruber B.S.// Phys. Rev. Lett. – 1996, v. 76, №3. - c. 459-462.

2.       W.G. Wolfer. Diffusion of point defects in a stress gradient. //Scripta METALLURGICA, 1971, 5, №11, р. 1017 – 1022.

3.            Абызов А.С., Слезов В.В., Танатаров Л.В. О роли вакансий в релаксации напряжений вокруг растущего включения новой фазы.// ФТТ, 1991, т. 33, №3. – с. 973 – 975.

4.            Александров Я.Н., Зотов М.И. Внутреннее трение и дефекты в полупроводниках. – Новосибирск, 1979.

5.            Алехин В.П. Физика прочности и пластичности поверхностных слоев материалов. М.:Наука, 1983.- 280 с.