Физика/1. Теоретическая физика
К.ф-м.н.
Галиахметов А.М.,
Донецкий национальный технический
университет, Украина
Точно интегрируемая однородная
изотропная космологическая модель в общей теории относительности
В работе в рамках проблемы существования
точно интегрируемых космологических моделей в общей теории относительности
(ОТО) с неминимально связанным скалярным полем рассматриваются анизотропные
модели для духового (ghost)
скалярного поля с учетом его потенциала и ультрарелятивистского газа. Интерес к
потенциалу скалярного поля V(Ф) в
общерелятивистских теориях гравитации обусловлен рядом обстоятельств: его ролью
в изотропизации анизотропных космологических моделей, его учетом в моделях с
частицеподобными решениями; модели с V(Ф)
естественно возникают в альтернативных теориях гравитации и супергравитации, в
теориях струн и бран; скалярный потенциал управляет инфляцией и активно
используется в моделях темной материи и темной энергии (виды применявшихся V(Ф) приведены в обзорах [1, 2]).
Присутствие ультрарелятивистского газа
в качестве дополнительного источника гравитационного поля обусловлено как тем
фактом, что Вселенная, вообще говоря, является многокомпонентной системой, так
и ранее полученными результатами (см., например, [3,4]), полученными в ОТО и
показавшие важность учета этой компоненты в эволюции космологических моделей.
Лагранжиан модели выбираем в виде:
![]()
![]() æ
æ![]() . (1)
. (1)
Здесь ![]() – скалярная кривизна; æ
– скалярная кривизна; æ ![]() – гравитационная постоянная Эйнштейна,
– гравитационная постоянная Эйнштейна, ![]() – постоянная
неминимальной связи;
– постоянная
неминимальной связи; ![]() – лагранжиан
ультрарелятивистского газа.
– лагранжиан
ультрарелятивистского газа.
Отметим, что уравнение скалярного поля,
соответствующее лагранжиану (1), при ![]() и
и ![]() будет
конформно-инвариантным.
будет
конформно-инвариантным.
Варьируя действие с лагранжианом (1) по ![]() и
и ![]() получим
получим
![]() æ
æ ![]() , (2)
, (2)
![]() , (3)
, (3)
где
![]()
![]() ,
,
![]() . (4)
. (4)
Здесь ![]() ;
; ![]() ,
, ![]() - плотность энергии и
давление ультрарелятивистского газа.
- плотность энергии и
давление ультрарелятивистского газа.
Для однородных изотропных открытых
моделей с метрикой
![]() ,
(5)
,
(5)
уравнения (2) и (3)
принимают вид
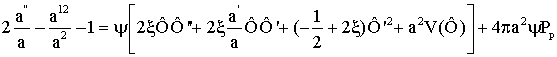 , (6)
, (6)
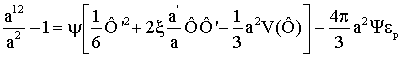 ,
(7)
,
(7)
![]() , (8)
, (8)
где ![]() æ
æ![]() æ
æ![]() , штрих означает дифференцирование по
, штрих означает дифференцирование по ![]() .
.
В метрике (5) для ультрарелятивистского
газа справедливо
![]() ,
, ![]() . (9)
. (9)
Потенциал скалярного поля V(Ф) выберем в виде
![]() æ
æ![]() , (10)
, (10)
где С2 = const > 0. Здесь следует, что в литературе наряду с V(Ф) > 0 рассматривался модели с V(Ф) < 0 [6 - 8].
Для ![]() получено точное
частное решение
получено точное
частное решение
![]() ,
, 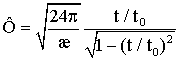 , (11)
, (11)
где t ![]() космическое
синхронное время
космическое
синхронное время ![]() ;
; ![]()
![]() постоянные интегрирования,
на которые накладывается условия:
постоянные интегрирования,
на которые накладывается условия:
![]() ,
, ![]() .
(12)
.
(12)
Решение (11) справедливо для ![]() , оно описывает космологическую модель, которые расширяется
от начальной сингулярности (t=-t0), достигает
максимума
, оно описывает космологическую модель, которые расширяется
от начальной сингулярности (t=-t0), достигает
максимума ![]() , а затем начинает сжиматься к финальной сингулярности
, а затем начинает сжиматься к финальной сингулярности ![]()
В классической монографии [9] приведено точное решение аналогичной задачи без учета скалярного поля:
![]() ,
, ![]() , (13)
, (13)
где ![]()
Сравнительный анализ полученного решения (11) с (13) показывает, что скалярное поле с потенциалом вида (10) создает эффект типа кривизны [10], так как эволюция модели (11) характерна не для открытой, а для закрытой космологической модели.
Литература:
1.
Sahni V., Starobinsky A.A. // IJMP. - 2000. – v. D 9.
– P. 373.
2.
Peebles P.J.E., Ratra B. // Rev. Mod. Phys. – 2003. – v. 75. – P. 599.
3.
Зельдович Я.Б.,
Новиков Н.Д. Строение и эволюция Вселенной. – М.: Наука, 1975.
4.
Захаров А.В. //
ЖЭТФ. – 1979. – т. 77. - № 2. – С. 434.
5.
Galiakhmetov A. M. // Gravitation and Cosmology. -
2007. – v.14 – № 3. – P. 190.
6.
Felder G.N., Frolov A., Kofman L., Linde A. // Phys.
Rev. D. – 2002. – v. 66, 023507; hep-th / 0202017.
7.
Kallosh R., Linde A., Prokushkin S., Shmakova M. // Phys.
Rev. D. – 2002. – v. 66, 1235503; hep-th / 0208156.
8.
Alam U., Sahni V., Starobinsky A.A., "Can dark
energy be decaying?", astro-ph / 0302302.
9.
Ландау Л.Д.,
Лифшиц Е.М. Теория поля. – –. Наука, 1973.
10.
Галиахметов
А.М.// Изв. вузов. Физика. –
2003. – №7. – с.23
Сведения об авторах
1.
Галиахметов Алмаз
Мансурович
Проспект
Победы, 90, кв. 20 г.Горловка,
Донецкая обл., Украина, 84646
Домашний
телефон: 8-06242-2-14-92
Рабочий
телефон: 8-06242-55-34-92
Автомобильно-дорожный
институт Донецкого национального
технического
университета.
завкафедрой
"Общенаучные дисциплины"
к.ф.
– м.н., доцент
2.
Вазанков Денис Борисович
Ул. Чубаря, 9, кв. 70 г. Славянск, Донецкая обл., Украина,
Домашний
телефон: 8-06262-2-04-51
Рабочий
телефон: 8-06242-55-34-92
Автомобильно-дорожный
институт Донецкого национального
технического
университета.
Ассистент
кафедры "Общенаучные дисциплины"
3.
Насаченко Роман
Викторович
ул.
Артиллеристов, 60, кв. 27, г. Горловка, Донецкая обл., Украина, 84614
Автомобильно-дорожный
институт Донецкого национального
технического
университета.
Студент IV курса, специальность "Автомобили и автомобильное
хозяйство"