Математика

Математическое моделирование

Айтчанов Б.Х., Айтчанова Ш.К.
Республика Казахстан,Казахский национальный технический университет

ВОПРОСЫ СХОДИМОСТИ РЯДОВ ВОЛЬТЕРРА, ПРИМЕНЯЕМЫХ В ТЕОРИИ НЕЛИНЕЙНЫХ СТОХАСТИЧЕСКИХ ДИНАМИЧЕСКИХ СИСТЕМ 

  Нелинейные стохастические динамические системы удобно часто представить функциональным уравнением вида

                                          ,                                     (1)

где  u(t) – входной  случайный процесс; z(t)-выходной случайный процесс; m(t)- белый шум с характеристиками   ,                           r11-интенсивность (высота) спектральной плотности белого шума.

Решение функционала (1) в  [1]  получено в виде следующего ряда

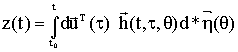                                   ,                                                  (2)

где матрица  определяется в виде

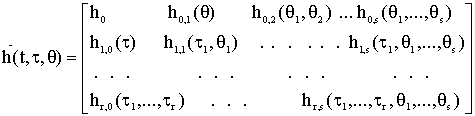                 ,       (3)

       ;

  .     (4)

Ряд (2) является описанием типа «вход-выход» стохастических динамических систем. В дальнейшем, для исследования свойств (2) необходимо определить связи между моделями типов «вход-выход» и «пространство состояний».

Уравнение (1) в методе «пространство состояний» представляется в форме стохастических дифференциальных  уравнений

                                    ,                                           (5)

где D-нелинейный оператор.

Рассмотрим конкретную форму уравнения (5), представленную в виде стохастических дифференциальных уравнений Ито

                    (6)

где постоянная матрица,-векторы, стандартный винеровский процесс,     непрерывные нелинейные функций.

Разлагая функции в сходящиеся в среднем  квадратичном ряды  и    уравнение (6) можно представить в эквивалентном интегральном виде

(7)

где       .                                                                             

Здесь первый интеграл в правой части понимается в смысле Стилтьеса, второй – в смысле Римана, третий – в смысле Ито. Причем во всех случаях интегральные суммы сходятся к соответствующим интегралам в среднем квадратичном.

  Связь между моделями вида  (6) и  (2) установим в виде следующего утверждения.

  Утверждение. Если существует  решение уравнения  (6) и оно единственно, то его можно представить в виде следующего стохастического ряда Вольтерра                            

                                               ,                                      (8)

где

          

.  (9)

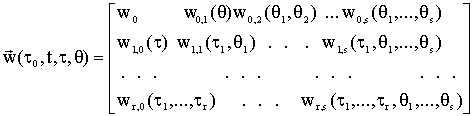                    ,    (10)

Элементы матрицы  определяются из уравнения  (6) или  (7) соотношениями вида:

                                                   

              ;

            ;                                                                                       

            ;                     (11)

             

              и т.д.

      Для доказательства утверждения будем решать уравнение  (7) методом последовательных приближений [2]. Пусть первое приближение решения уравнения  (7) имеет вид

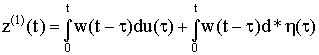                            .                                  (12)

Подставляя (12) в  (7), получим второе приближение

                                    .                                       (13)

Матрица  и векторы ,имеют структуру, аналогичную матрице  (10) и векторам  (9).

Элементы матрицы определяются в виде следующих соотношений:

                

;

   

               и т.д.

Аналогично продолжая процедуру последовательного приближения, получим n-e приближение решения уравнения  (7):

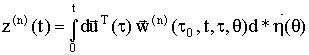                         .                                       (14)

Элементы матрицы   определяются из следующих рекуррентных соотношений:

             

,(15)

          ;                  

                  

  и т.д.

   Таким образом, решения уравнения (6) можно путем последовательного приближения представить в виде ряда  (8). Элементы матрицы  определяются на основании (11) соотношениями (15)
, что доказывает сформулированное выше утверждение.

Полученный ряд (8) является формальным. Для того, чтобы ряд (8), стал действительным решением уравнения (6), следует получить условие сходимости этого ряда к решению уравнения (8) или (7).

  Для этого уравнение (7) преобразуем в виду

,                                  (16)      

где                   ;

                               ; .

  Полученные результаты анализа сходимости ряда (8) к решению уравнения (16) приведены в виде следующего утверждения.

Утверждение. Если выполняются неравенства

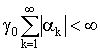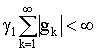               ,,,,,               (17)

где постоянные g0, g1 определяются  свойствами системы в виде

                          ,  ,                             (18)

а постоянные  величины , , свойствами входных и выходных процессов

                           (19)

то ряд (8) сходится  в среднем  квадратичном.

 

Литература:

1. Айтчанова Щ.К. Функциональные ряды в теории стохастических нелинейных систем // Materialy IV mezinarodni vedecko-prakticka konference “Efektivni nastroje modernich ved -2008”. - Dil 18. Technicke vedy. Moderni informacni  technologie :Praha. Publishing House  “Education and Science”. st. 6-10.

2. Попков Ю.С., Киселев О.Н., Петров Н.П., Шмульян Б.Л. Идентификация и оптимизация нелинейных стохастических систем. М.: Энергия, 1976, 438 с.