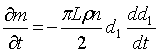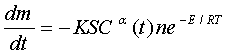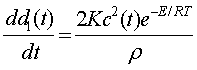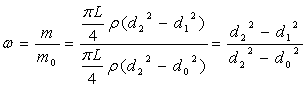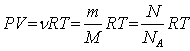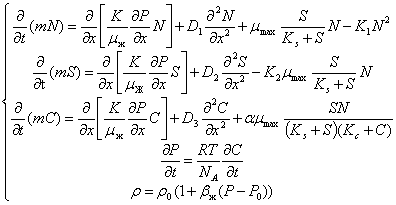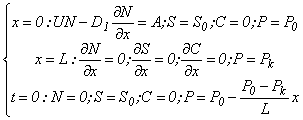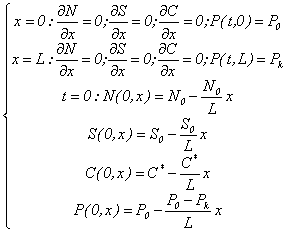Биологические науки/6. Биоинженерия и биоинжорматика.
Д.х.н., профессор Гинак А.И.
Санкт- Петербургский Государственный
Технологический институт ( технический университет). Россия.
К.т.н., Кузнецова С.Н.
Санкт- Петербургский Университет
Информационных Технологий, Точной механики и Оптики( ИТМО). Россия
К.т.н., доцент Милованович Е.В.
Санкт- Петербургский Университет
Информационных Технологий, Точной механики и Оптики( ИТМО). Россия
Магистр Ващенко В.В
Санкт- Петербургское открытое
акционерное общество Севморгео. Россия
Моделирование биотехнологических процессов повышения
нефтеотдачи пластов.
Методы нефтедобычи
Выделяют три метода, или фазы нефтедобычи в зависимости от давлений
в нефтеносном пласте и способов
его поддержания.
Первичный метод
Нефть поступает из пласта
под действием естественных сил, поддержи-
вающих высокое давление
в пласте, например,
замещение нефти подземными водами, расширение газов, растворенных в нефти, и др. Коэффициент извлечения
нефти (КИН) при этом методе составляет 5-15 %.
В одних случаях давление в пласте достаточно для того, чтобы нефть поднялась до поверхности. В других случаях требуется использование погружных насосов, либо штанговых (используются вместе
со станком-качалкой), либо электрических.
Вторичный метод
После исчерпания естественного ресурса поддержки давления, когда оно уже недостаточно для подъема нефти, начинается применение вторичных методов. В пласт подводят внешнюю энергию
в виде закачиваемой жидкости (пресной воды), натурального или попутного газа Газлифт или газов атмосферы (воздух,
углекислый газ). Методы достигают КИН около 30%, в зависимости
от свойств нефти и пород резервуара. Суммарный КИН после применения
первичных и вторичных
методов обычно в пределах 35-45%. Закачивание
воды значительно
повышает обводненность, иногда вплоть до 95%. Это приводит
не только к экономическим потерям, но и несёт серьёзную
экологическую опасность.
Третичный метод
Третья фаза добычи нефти увеличивает подвижность нефти для увеличения нефтеотдачи. Один из вариантов третичных методов, TEOR, связан с нагревом нефти в пласте
для уменьшения ее вязкости. Часто применяется закачивание водяного пара, иногда также используют
сжигание части нефти на месте (прямо в пласте).
Также в пласт могут закачиваться ПАВ (Детергенты) для изменения
поверхностного натяжения между водой и нефтью. Данный
метод позволяет повысить КИН еще на 5% - 15%.
Третичный метод начинают использовать, когда вторичный перестает быть адекватным, но только при условии, что добыча нефти остается рентабельной. Таким образом, использование третичного метода зависит как от стоимости выбранного способа
извлечения, так и от цен на нефть.
В данной работе будет рассмотрен еще один способ интенсификации добычи нефти на третьей фазе – с помощью биологически активной фазы. В нагнетаемую воду вводятся
микроорганизмы и питательная среда. Вследствие эволюции
популяции микроорганизмов физические условия в этих слоях изменяются, что может привести
к облегчению вытеснения
из них нефти. При размножении микроорганизмов , увеличении популяции
и биосинтезе газообразных веществ увеличивается и давление в пласте. Продуктом микробиологического синтеза
также является уксусная кислота, которая
растворяет известняк в порах. Внутри
поры можно рассмотреть следующую
химическую реакцию:
2CH3COOH + CaCO3 → (CH3COO)2Ca + H2O + CO2 (A)
В результате реакции образуется соль ацетата кальция,
которая является раст- воримой. Увеличивается таким образом проницаемость слоя и общая отдача коллектора.
Будем считать, что процесс фильтрации проходит горизонтально, то есть имеются две скважины, движение флюидов
происходит прямолинейно-параллельно. Одна для нагнетания воды, микроорганизмов и питательной среды; другая для добычи нефти. Пласт рассматриваемой породы можно представить как параллелепипед.
1.1
Модель поры внутри породы
В нашей модели будем считать, что внутри породы поры имеют вид трубочек-
цилиндров, лежащих не хаотично, а горизонтально и параллельно. Размер пор для простоты будет
взят одинаковым. При
этом трещины, которые могут быть
в пласте, учитываться не будут. На стенках поры имеются отложения известняка. Таким образом,
пора-цилиндр имеет толщину стенки,
которая изменяется при проходящей в поре реакции (A) с уксусной кислотой.
Таким образом, масса известняка, находящегося в пласте в начальный момент будет вычисляться следущим образом:
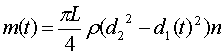 (1)
(1)
r - плотность известняка, кг/м3;
L – длина образца,
м;
d2 – наружный диаметр поры, м;
d1 – внутренний диаметр поры, м;
n – количество
пор в рассматриваемом элементе пористой
среды.
Во времени будет меняться
масса образца известняка, так как внутренний диаметр может изменяться при растворении известняка уксусной кислотой, а
также при закупоривании микроорганизмами. Изменение массы известняка за единицу времени будет выражаться следующим
образом: необходимо взять производную массы по времени от выражения (1):
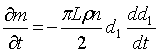 (2)
(2)
С другой стороны, скорость
изменения массы известняка будет также за-
висеть от скорости его растворения в порах, то есть
от концентрации уксусной
кислоты:
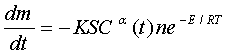 (3)
(3)
где
S – площадь поверхности
известкового отложения, м2.;
C – концентрация
уксусной кислоты, кг/м3;
a - порядок химической реакции ( a = 2
);
K –
константа скорости химической реакции;
E –
энергия активации, Дж;
T –
температура, К;
R –
универсальная газовая постоянная, Дж×
(моль×К) –1.
В случае
реакции (A) порядок химиеской реакции α = 2, так как уксусной кислоты
для протекания данного процесса необходимо в два раза больше известняка.
Площадь известкового отложения, вступающего
в реакцию с уксусной
кислотой внутри поры, будет изменяться
во времени:
S(t) = Lπd1(t) (4)
Подставляем выражение для площади поры (4)
в уравнение (3).
Приравнивая формулы
описания изменения массы известняка (2) и (3),
получаем вы- ражения, по которому изменяется диаметр поры во времени:
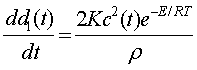 (5)
(5)
Если все константы из формулы (5) переобозначить одной новой константой,
E
2Ke−RT
 K = (6)
K = (6)
ρ
тогда диаметр поры изменяется со временем
следующим образом:
 dd1(t) dt
dd1(t) dt
= KC2(t) (7)
1.2
Моделирование биохимических процессов в призабойной зоне скважины
Рассматривается наиболее распространенная форма записи
закона, учи-тывающая
насыщение культуры
по питательному субстрату - модель
Моно. Пусть изменение проницаемости зависит от двух параметров. Проницаемость снижается из-за закупорки пор бактериями
согласно уравнению:
k(N ) = k0(b0 + b1e−b2N )
где, k0 – начальный
коэффициент проницаемости;
N – концентрация микроорганизмов;
b0 ,
b1 , b2 – коэффициенты, характеризующие интенсивность снижения проницаемости за счет образования пробок биомассы.
Наоборот, проницаемость увеличивается за счет расширения
поры при реакции (A). Учитывая оба фактора получаем:
k(t) = k(N ) · k(d1)
k(d1) = ad2, где a – коэффициент пропорциональности
Тогда проницаемость будет изменяться следующим образом:
dk(t) dt
= k(d1)
dk(N ) dt
+ k(N )
dk(d1) dt
 Получаем следующие
зависимости:
Получаем следующие
зависимости:
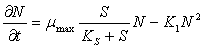 (8)
(8)
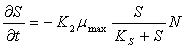 (9)
(9)
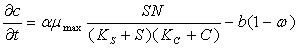 (10)
(10)
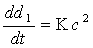 (11)
(11)
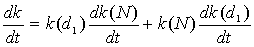 (12)
(12)
 (13)
(13)
N – концентрация микроорганизмов,
ед/м3
S – концентрация субстрата,
кг/м3
µmax, K1, K2, Kc, Ks, α – коэффициенты, характеризующие кинетику био- химических реакций
k – проницаемость (м2)
µ – вязкость нефти (Па · с)
Pk – пластовое давление (Па) P0 – забойное
давление (Па)
L – длина пласта (м)
B – ширина пласта (м)
h – толщина пласта (м)
b – уменьшение концентрации ацетата при
полном растворении известняка
ω – доля нерастворенного известняка
b (1 − ω) – уменьшение концентрации ацетата за счет растворения им известняка
m0 – масса известняка в начальный момент времени
m – масса известняка в данный
момент времени
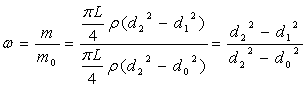
d0 – внутренний диаметр поры в
начальный момент времени
Параллельно изучалось уменьшение
пористости коллектора в зависимости от концентрации находящихся в нем микробных клеток. Падение
пористости было вызвано закупоркой каналов
растущей колонией
микроорганизмов.
Текущая пористость m определяется как отношение
m = Vж
Vобр
Vж – объем жидкости, находящейся в образце пористой среды,
т. е. объем сообщающихся полостей,
Vобр – объем образца.
Поскольку
пористость и проницаемость очень тесно взаимосвязаны между собой, то
естественно было предположить, что они меняются по схожим законам. Была предложена следующая оценочная функция регрессии .
m(N ) = m0(a0 + a1e−a2N )
где, a0, a1, a2 – оценки коэффициентов снижения пористости за счет образования пробок биомассы.
Параметры функции регрессии определялись опытным
путём..
N – концентрация микроорганизмов;
Процесс внутри пласта можно считать изотермическим, поэтому можно
воспользоваться уравнением Клайперона-Менделеева
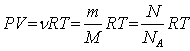 (14)
(14)
Где 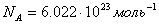 - постоянная Авогадро, М- молярная масса газа.
- постоянная Авогадро, М- молярная масса газа.
Если обе части уравнения поделить на объем V , то получится зависимость давления газа от его
плотности.
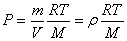
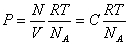 (15)
(15)
где ρ – плотность газа, C - концентрация газа.
Нам необходимо, чтобы со временем давление увеличивалось, для того чтобы отдача нефти была больше.
Зависимость изменения давления во времени получаем, взяв производную по времени от формулы (15):
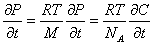 (16)
(16)
1.3
Система уравнений
Система нелинейных неоднородных дифференциальных уравнений в частных производных второго порядка представляет задачу о распространении популяции
микроорганизмов в пористой
среде:
\
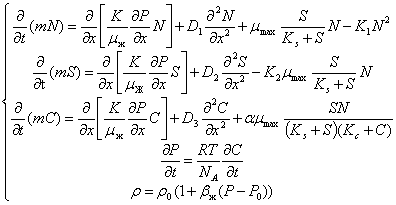 (17)
(17)
В первом уравнении системы концентрация микроорганизмов увеличивается во времени за счет размножения по модели Моно и одновременно с этим уменьшается за счет
лизиса и конкуренции. Второе
уравнение описывает
изменение концентрации питательных
веществ. Концентрация уменьшается за счет
поглощения субстрата микроорганизмами. Третье уравнение системы
описывает изменение концентрации продукта метаболита реакции.  - экономический коэффициент. В четвертом уравнении рассматриваются газы, выделяющиеся в процессе
реакции. близки к этому. Четвёртое уравнение получилось из закона Клайперона-Менделеева (16). Необходимо было получить решение системы
и посмотреть, как повышается давление.
- экономический коэффициент. В четвертом уравнении рассматриваются газы, выделяющиеся в процессе
реакции. близки к этому. Четвёртое уравнение получилось из закона Клайперона-Менделеева (16). Необходимо было получить решение системы
и посмотреть, как повышается давление.
Случай непрерывного нагнетания бактериальной суспензии в пласт
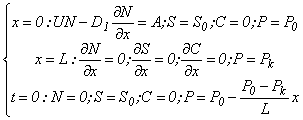 (18)
(18)
Случай периодического нагнетания бактериальной суспензии в пласт
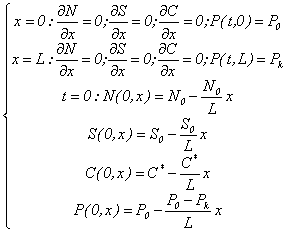 (19)
(19)
Функциональные зависимости, описывающие изменение пористости и про- ницаемости
среды в присутствии микроорганизмов были получены на основа- нии статистической обработки
данных эксперимента. Изучалось
уменьшение пористости
коллектора в зависимости от концентрации находящихся в нем микробных
клеток. Падение пористости
было вызвано закупоркой каналов
растущей колонией микроорганизмов.
Клетки микроорганизмов растут и делятся очень быстро.
Некоторые бактерии дают новую генерацию каждые 30 мин. Это значит, что за 5 ч из одной клетки может образоваться примерно
1000 клеток. Масса одной бактерии равна 0.2 · 10−9 мг, но масса образованной из нее биомассы через 16 ч равна уже 1 мг. В течение суток одна клетка образует
около 1 кг биомассы,
а в течение 1
сут - такое количество биомассы, которое трудно было бы вместить в один железнодорожный состав.
Плотность клеток
микроорганизмов очень близка к плотности
водной среды, в которой
они растут, и при анализе теплопередачи в дисперсионных культурах бактерий
и дрожжей, обычно
имеющих диаметр эквивалентной сферы меньше 10 мкм, культуральную среду можно рассматривать как однородную
водную фазу.
2
Решение задачи о распространении популяции микроорганизмов
в пористой среде нефтяного
пласта
2.1
Численное решение поставленной
задачи
Систему уравнений (17) решалась численным методом конечных
разностей с помощью математического пакета Wolfram Mathematica под операционной системой OS X. Решение
будем искалось для начальных
данных (18, 19). Значения
всех параметров были получены
опытным путём.
Систему уравнений (17)
аппроксимировалась разностной
схемой на двумерной
пространственно-временной сетке. Для нахождения решений на сетке
были составлены рекуррентные соотношения
для уравнений.
Часть уравнений были подставлены
напрямую друг в друга
Результаты численного моделирования
В ходе решения
были получены профили распределения компонентов биоценоза по длине пласта при периодическом и непрерывном нагнетании культуральной
жидкости в коллектор.

Рис. 1. Увеличение давления от начала координат до граничной
точки
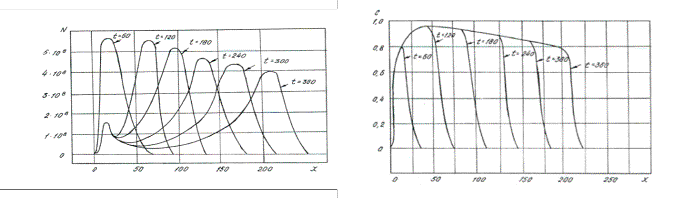 Рисунки (2) показывают распределение концентрации микроорганизмов,
субстрата и метаболита по длине пласта при непрерывном нагнетании культу- ральной жидкости в коллектор.
Рисунки (2) показывают распределение концентрации микроорганизмов,
субстрата и метаболита по длине пласта при непрерывном нагнетании культу- ральной жидкости в коллектор.
2) 3)
Рис.
2. Распредение концентрации микроорганизмов и метаболита
по длине пласта при непре- рывном нагнетании
культуральной жидкости в скважину
Рисунки (3)
показывают распределение компонентов системы по длине пласта при периодическом нагнетании культуральной
жидкости в скважину.
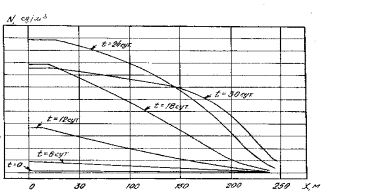
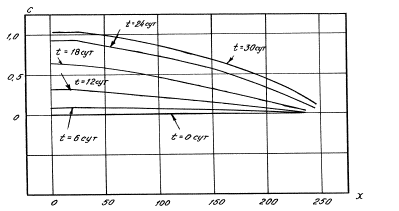
Рис.
3. Распредение концентрации микроорганизмов и метаболита
по длине пласта при периодическом нагнетании
культуральной жидкости в скважину
В результате мы видим, что при использовании биологически активной фазы при добыче нефти, давление в коллекторе увеличивается из-за размножения микроорганизов, а также увеличивается дебит нефти. Это позволяет
использовать текущие коллекторы гораздо
более плодотворно.
Результаты работы могут быть внедрены в организациях и на предприятиях, занимающихся лабораторными исследованиями и техническим производством
микроорганизмов при добыче нефти.
Литература
1. Аметов А.М., Енотов В.М. О математическом моделировании биогенных про- цессов в нефтяных
пластах // Известия АН СССР. Механика жидкости и газа. – 1981. - № 6. – с. 84-91
2. Розанова Е.П., Кузнецов С.И. Микрофлора нефтяных месторождений. Москва. Наука, 1974. 198 с.
3. Холоднов В.А., Лукина М.В., Милованович Е.В. Моделирование биотехно- логических и фильтрационных процессов повышения нефтеотдачи пластов
// Известия СПбГТИ (ТУ). – 2011. – № 11. – с. 69-72
4. Котенев Ю.А., Загидуллина Л.Н., Андреев В.Е. Микробиологический ме- тод
уеличения нефтеотдачи
пластов на основе
активного ила биологических очистных сооружений // Нефтяное хозяйство.
– 2004. – №4. с. 48-50
5. Ризниченко Г.Ю. Математические модели в биофизике и экологии. Москва- Ижевск, 2003, 184 стр.
6. Базыкин А.Д. Математическая биофизика взаимодействующих популяций. Москва, Наука, 1985
7. Тихонов А.Н.,
Самарский А.А. Уравнения математической физики. Москва.
Изд-во МГУ, 1999 – 799 с.
8. Владимиров В.С., Жаринов В.В. Уравнения математической физики. Москва, 2004, 400 с.
9. Эванс Л.К. Уравнения с частными
производными. Университет Калифор- нии, США
/ Пер. с англ. –
Новосибирск: Рожковская Т., 2003. –
562 с.
10. Мареев В.В., Станкова Е.Н.
Основы методов конечных
разностей. – СПб.: Изд-во
С-Петерб. ун-та, 2012. 64 с.
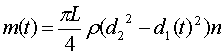 (1)
(1)