К.т.н. Мезенцев К.Н.

Московский автомобильно-дорожный государственный технический университет (МАДИ)

Современные методы моделирования работы компьютерных сетей

Моделирование компьютерной сети как системы массового обслуживания

Компьютерная сеть как система массового обслуживания (СМО) может быть рассмотрена в виде наборов каналов обслуживания [3]. Такой канал состоит из очереди – заявок. В качестве заявки выступает блок байтов при передаче данных или задание для обработки процессором. В дальнейшем будем использовать в качестве понятия заявки универсальный термин информационный кадр.

При этом канал обслуживания можно рассматривать как систему обработки данных, которая характеризуется набором параметров:

T – период времени наблюдения за каналом

A – число информационных кадров поступивших в канал на обслуживание

С – число информационных кадров на выходе канала обслуживания

Для оценки работоспособности используют такие характеристики как

Это интенсивность поступления информационных кадров в канал обслуживания.

Пропускную способность канала определим как

Информационный кадр поступает в процессор для обработки. Структура канала обслуживания показана на рисунке 1. На рисунке ЦПУ (Центральное Процессорное Устройство) процессор обработки информационного кадра.

При моделировании канала обслуживания используются следующие параметры:

Поступая в процессор информационный кадр, задерживается для обработки. Если время обработки равно B то можно ввести параметр U – как параметр загрузки процессора. Этот параметр определим в виде:

Здесь T время наблюдения за процессором. Для оценки производительности канала воспользуемся также коэффициентом S, который позволяет определить время обслуживания информационных кадров, поступивших на выход процессора. Это значение определяется по формуле

Работу канала обслуживания с учетом выше указанных зависимостей можно оценить с помощью зависимости:

Этот параметр представляет собой коэффициент использования системы. Этот коэффициент является частным случаем закона Литтла.

Так если информационный кадр находился в канале обслуживания от момента постановки в очередь до момента выхода время W то с учетом времени наблюдения за каналом получим среднее число запросов выполненных каналом в виде:

Среднее время канала обслуживания на один запрос будет равно:

С учетом указанных зависимостей закон Литтла для канала обслуживания примет вид:

Таким образом, согласно закону Литтла среднее число информационных кадров в канале должно быть равно произведению пропускной способности системы на среднее время обслуживания на один запрос.

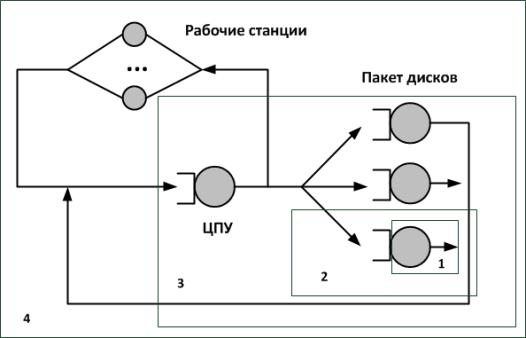
Рисунок 1- Компьютерная сеть и сервер

Оценить работу вычислительной системы с помощью закона Литтла можно рассматривая ее с разных точек зрения, так как это показано на рисунке 1.

1 – Подсистема состоящая из одного ресурса. В качестве которого может выступать жесткий диск рабочей станции сети.

2 – Ресурс с очередью. Это жесткий диск или оперативная память рабочей станции с очередью запросов на обслуживание.

3- Рабочая станция, или сервер с процессором и долговременной и оперативной памятью.

4 – Компьютерная сеть в целом равноправным доступом или выделенным файл-сервером.

Чтобы учесть реакцию пользователя рабочей станции закон Литтла позволяет вывести зависимость для параметра R в виде:

Здесь Z – время реакции пользователя рабочей станции.

Сервера и рабочие станции предоставляют пользователям сети доступ к определенному ресурсу. Типичным примером такого ресурса является жесткий диск сервера и рабочей станции.

Для интенсивности доступа к ресурсу введем параметр

Здесь C_k – число обращений к ресурсу k. C учетом приведенных ранее зависимостей пропускную способность ресурса к можно определить как

Оценить потребность в течении определенного в k ресурсе можно с помощью зависимости

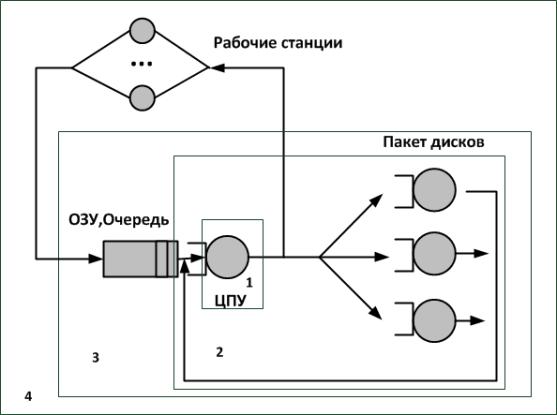
Рисунок 2 - Сервер, работающий в режиме разделения времени

Рассмотренные параметры могут быть использованы при оценке работы сети с сервером работающим в режиме разделения времени.

На рисунке 2 выделено четыре подсистемы для анализа работы сервера и сети.

1 – центральный процессор сервера

2 – центральный процессор сервера с очередью и пакет жестких дисков с очередями.

3 – Очередь поступивших для обработки информационных кадров в оперативной памяти процессор с пакетом дисков.

4. – Рабочие станции, подключенные к серверу.

Распределенные вычисления

Обработка данных в компьютерной сети может выполняться локально на сервере или на отдельной рабочей станции. Как известно сеть представляет собой объединение вычислительных ресурсов, поэтому представляет интерес исследовать методику организации распределенных вычислений в сети, когда отдельная задача разделяется на подзадачи для обработки которых используются сетевые вычислительные ресурсы.

Рассмотрим N машин, связанных в произвольную компьютерную сеть. Все машины вместе выполняют некоторый распределенный алгоритм вычислений, который мы будем называть базовым алгоритмом [4]. Каждая машина может быть либо в активном состоянии, выполняя базовые вычисления, либо в пассивном состоянии, если она завершила свою часть распределенного вычисления. Активная машина, выполняющая базовые вычисления, может посылать информационный кадр (сообщение) каким-либо другим машинам в сети, передавая им часть работы. Информационные кадры получаются адресатом после некоторой задержки в сети без потерь. Если пассивная машина получает информационный кадр, она становится активной, активная машина, получившая информационный кадр, остается активной и продолжает вычисления.

Из активного состояния переход машины в пассивное состояние может произойти по завершении ее части общих вычислений в любой момент. Прием информационного кадра является единственным событием, которое переключает машины из пассивного в активное состояние. Отсюда следует, что ситуация, в которой все машины пассивны, а в сети нет сообщений, посланных ранее какой-нибудь из активных машин, является стабильной: распределенное вычисление завершено.

Для моделирования работы сети, выполняющей распределенные вычисления требуется использовать алгоритм распределенного завершения. Суть алгоритма состоит в том, чтобы некоторая машина с определенным номером, обнаружила, что система пришла в стабильное состояние как можно быстрее. Тестируемая машина должна использовать информацию от остальных машин об их состоянии. Алгоритм определения распределенного завершения не может быть просто проверкой текущего состояния всех машин в сети и принятия решения о завершении вычислений, если все машины отрапортовали о том, что они пассивны.

Это обусловлено тем, что:

Мгновенно такую проверку выполнить в распределенной системе невозможно.

В канале могут находиться задержанные сообщения базового алгоритма, которые могут активизировать перешедшую в пассивное состояние машину, которая уже послала рапорт о своем пассивном состоянии.

Для исследования работы распределенной вычислительной системы, введем понятие зондирования.

Зондирование может быть инициировано выделенной машиной с номером n в любом состоянии всей сети, при любом распределении активностей в ней. Поэтому запущенный алгоритм зондирования может дать отрицательный результат, если сеть машин не находится в стабильном состоянии. Обычно алгоритм зондирования запускается первой – нулевой машиной периодически: если очередной сеанс зондирования оказался неудачным, инициируется следующий раунд.

Одно из решений задачи распределенного завершения было предложено голландским ученым Э. Б. Дейкстрой. Этот алгоритм работает на произвольном числе машин, пронумерованных от 0 до n, связанных в виртуальное кольцо. Алгоритм состоит из повторения циклов зондирования сети посылкой зонда (токена) по кольцу машин. Данный распределенный алгоритм состоит из следующих правил, которые гарантируют решение проблемы:

Каждая машина в сети поддерживает счетчик Counter. Каждая посылка сообщения базового алгоритма увеличивает Counter на 1; прием базового сообщения уменьшает Counter на 1. Таким образом, сумма всех счетчиков в сети машин в некоторый момент времени равна числу сообщений, задержанных в сети.

Если сумма значений счетчиков 0, то никаких базовых сообщений в сети нет.

Машина 0 инициирует шаг зондирования в любой момент и в любом своем состоянии, посылая токен со значением 0 машине n - 1. Каждая машина i задерживает полученный токен до тех пор, пока не станет пассивной. После этого значение токена увеличивается на Counter, и токен передается машине i-1.

Машины, и токен окрашены в определенный цвет. Вначале все машины и токен белые. Машина, получившая базовое сообщение, становится черной. Когда машина передает токен, она становится белой. Если черная машина передает токен, токен становится черным, в противном случае токен сохраняет свой цвет.

Когда машина 0 получает свой токен, прошедший по кольцу всех машин, очередной цикл зондирования закончен. Машина 0, получив токен, ждет, пока она не перейдет в пассивное состояние. После этого она делает заключение о завершении базовых вычислений в сети машин при следующих условиях:

сама машина 0 белая;

полученный токен белый;

сумма значений токена и счетчика Counter машины 0 равна 0.

В противном случае завершения на этом цикле не обнаружено, машина 0 запускает новый цикл зондирования.

Анализ трафика компьютерной сети

Компьютерная сеть может быть рассмотрена как совокупность узлов, в качестве которых выступают сервера и рабочие станции [1,2].

В этом случае компьютерную сеть рассматривают как граф, а процессы связанные с маршрутизацией могут рассмотрены как Марковские.

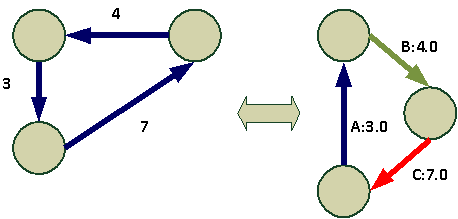
Рисунок 3 - Сеть с тремя узлами

На рисунке 3 показана компьютерная сеть, состоящая из трех узлов. Под узлом будем понимать рабочую станцию или сервер. Ребра графа взвешены коэффициентами, которые соответствуют числу информационных кадров, циркулирующих в сети.

Далее подвергая трансформацию граф, получим граф, в котором дуги трафика условно обозначены латинскими буквами, а через двоеточие указано число информационных кадров в сегменте сети. Для анализа трафика сети произведем трансформацию согласно рисунку 3.

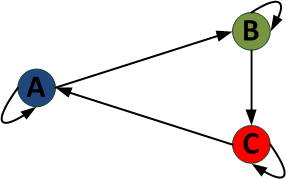
Рисунок 4 – Трансформация, граф состояний трафика

Смысл трансформации трафика сводится к анализу состояния трафика. Каждая вершина графа – состояние трафика.

Так согласно рисунку 4 трафик из состояния A переходит в состояние B, из состояния B в состояние C и наконец из состояния C в состояние A. Кроме того трафик может не менять состояния все состояния замкнуты на себя.

Переход из одного состояния в другое может происходить с определенной вероятностью. Это вероятность указывается на ребрах графа состояния, таким образом возникает Марковская цепь. В такой цепи переход из одного состояния в другое происходит без учета истории. Марковская цепь может быть представлена также в виде матрицы, так как это показано на рисунке 5.

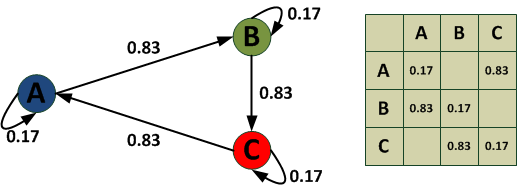
Рисунок 5 - Марковская цепь

При использовании Марковской цепи в виде матрицы переход читается по принципу Столбец – Строка. Например, переход из состояния B в состояние C происходит с вероятностью равной 0,83. Отсутствие значения в матрице означает невозможность перехода.

Таким образом, применяя Марковскую цепь, можно оценить с определенной вероятностью сколько информационных кадров пройдет в определенном направлении сети для этого используется зависимость

Здесь x – вектор размера n х 1, A – матрица вероятностей размера n х n, а b вектор значений информационных кадров для определенного состояния размера n х 1. Здесь n – число состояний.

Для рассматриваемого случая численный анализ трафика примет вид:

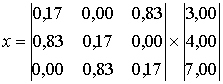
Анализируя Марковскую цепь можно выделить ряд особенностей трафика.

Тупиковые состояния это такие состояния, из которых невозможен дальнейший переход, что ведет накапливанию информационных кадров в узлах сети и как следствие к перегрузке сети и потере данных.

Периодические состояния это два состояния связанные взаимными переходами с одинаковой вероятностью. Ситуация зацикливания движения информационных кадров в сети.

Переходное состояние. Это такое состояние, из которого информационный кадр может перейти в другое состояние, но не может больше в него вернуться никогда. Эта ситуация соответствует посылке информационного без возможности его возврата с исходное состояние по тому же маршруту.

Замкнутый граф состояния - любое состояние может быть достигнуто из любого произвольного состояния. Например, сеть в которой можно выбрать произвольные маршрут движения информационных кадров.

Анализируя матрицу вероятностей cделать также ряд существенных выводов о характере протекания сетевого трафика.

Анализируется сумма вероятностей по определенному столбцу. Так если сумма дает значение равное 1 то говорят о стохастической матрице вероятностей. Если это значение не равно 1 то возможно два варианта.

Значение меньше 1 общее число информационных кадров со временем стремится к нулю.

Значение больше 1 общее число информационных кадров со временем в сети стремится к бесконечности.

Кроме того, если граф состояний замкнутый и не содержит периодических состояний, независимо от начального состояния трафик сети стремится с определенному установившемуся распределению.

Литература:

1. Менцев К.Н. Моделирование в примерах и задачах./К.Н. Мезенцев. LAP

LambertAcademic Publishing, 2013. – 205 с. – ISBN 978-3-8473-7656-9.

2. Мезенцев К.Н. Автоматизированные информационные системы: Учебник/К.Н. Мезенцев. - М.–Издательский центр «Академия», 2010 – 176с. – ISBN 978-5-7695-6671-4

3. Мишенин, А.И. Теория экономических информационных систем:

Учебник. — 4-е изд., доп. и перераб/ А.И. Мишенин - М.: Финансы и статистика, 2002. - 240 с. – ISBN 2-279-01987-9.

4. Карпов Ю. Имитационное моделирование систем. Введение в моделирование с AnyLogic 5./Ю. Карпов – Спб.: БХВ Питербург, 2005. – 390 с. – ISBN 978-5-94157-148-2.