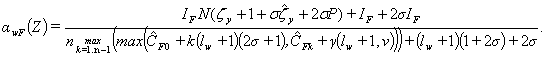Математика / 5. Математическое моделирование

к.т.н. Крючин О.В.

Тамбовский государственный университет им. Г.Р. Державина, Россия

Аналитическая модель параллельных информационных процессов обучения искусственных нейронных сетей использующих метод полного сканирования

В работах [1-3] описаны информационные процессы параллельного подбора весовых коэффициентов методом полного сканирования (полного перебора). Для оценки эффективности этих процессов разработана описываемая ниже аналитическая модель.

Количество мультипликативных операций, которые производит последовательный алгоритм полного сканирования можно записать следующим образом:

	(1)

где — к-во операций, необходимых для последовательного вычисления невязки , , — -ые выходные вектора моделируемого объекта и ИНС, — количество строк в обучающей выборке, — количество выходов объекта (размерность векторов и ), — число итераций алгоритма (информационный процесс раз выполняет вычисление невязки, а для организации цикла ему требуется операций — по 2 на каждой итерации, вперед и назад) [2].

Для вычисления количества мультипликативных операций, производимых информационными процессом полного сканирования, необходимо рассмотреть этапы, из которых он состоит:

1. инициализация;

2. передача данных с ведущего ИР-элемента (элемента информационного ресурса, в качестве которого может выступать узел кластерной системы или компьютер вычислительной сети) на прочие;

3. перебор значений весовых коэффициентов , принадлежащих данному ИР-элементу;

4. передача данных со всех ИР-элементов на ведущий;

5. выбор ведущим ИР-элементом оптимальной конфигурации.

На первом этапе на ведущем ИР-элементе происходит аддитивных операций (— число весов сети — для организации цикла и для присвоения), на втором — мультипликативных и аддитивных. На неведущих на втором этапе происходит мультипликативных и аддитивных операций, но начаться они могут лишь после того, как ведущий ИР-элемент отправит данные, поэтому на неведущем ИР-элементе происходит мультипликативных операций. Здесь — коэффициент, который прямо пропорционален времени, затрачиваемому на одну мультипликативную операцию и обратно пропорционален времени, затрачиваемому на одну аддитивную (мультипликативная операция занимает в раз больше времени, чем аддитивная и, следовательно, одну мультипликативную операцию можно заменить аддитивную и наоборот) [4].

Количество операций на третьем этапе аналогично количеству операций, выполняемых последовательной версией алгоритма (за исключением того, что число итераций — для ведущего ИР-элемента и для прочих).

На четвертом этапе ведущему ИР-элементу необходимо получить лучшие весовые коэффициенты и соответствующее им значение невязки с каждого ИР-элемента, поэтому он делает мультипликативных и аддитивных операций, а неведущий — мультипликативных и аддитивных. Кроме того, ведущий ИР-элемент должен ожидать отправку.

На пятом ведущий ИР-элемент делает аддитивных операций. Если привести аддитивные операции к мультипликативным, то можно получить выражения, приведенные в табл. 1.

Таблица 1. Число мультипликативных операций на различных этапах информационного процесса.

Этап	Ведущий ИР-элемент	Неведущий (-ый) ИР-элемент
1
2
3
4
5

До начала получения ведущим ИР-элементом весовых коэффициентов и значений невязки он осуществляет 3 этапа (обозначим общее количество операций ), а прочие — 4 (обозначим общее количество операций ). Для выполнения первых 2 этапов ведущий ИР-элемент производит , а -ый — операций.

Кроме того, необходимо учитывать время передачи невязки и весовых коэффициентов. Поскольку получение завершается после того, как значение невязки будет послано самым медленным процессором, то, для информационного процесса, использующего параллельное вычисление невязки, требуется операций, где вычисляется по формуле

	(2)

Исходя из вышесказанного, эффективность параллельного информационного процесса обучения можно выразить формулой

	(3)

Таким образом, аналитическая модель выглядит следующим образом

	(4)

Список литературы

1. Крючин О.В., Арзамасцев А.А., Королев А.Н., Горбачев С.И., Семенов Н.О. Универсальный симулятор, базирующийся на технологии искуственных нейронных сетей, способный работать на параллельных машинах / О.В. Крючин [и др.] // Тамбов: Вестн. Тамб. ун-та. Сер. Естеств. и техн. науки. 2008. – Т.13, Вып. 5. – C. 372-375.

2. Крючин О.В. Параллельный алгоритм полного сканирования обучения искусственных нейронных сетей // В мире научных открытий, Красноярск, 2010, №6.3 (12), C. 72-79.

3. Крючин, О.В. Параллельные алгоритмы обучения искусственных нейронных сетей / О.В. Крючин // Матер. XV междун. конф. по нейрокибернетике. Т. 2. Симпозиум «Интерфейс ''Мозг-Компьютер''», 3-й Симпозиум по Нейроинформатике и Нейрокомпьютерам. – Ростов-н/Д. 2009. – C. 93-97.

4. Крючин, О.В. Сравнение эффективности последовательных и параллельных алгоритмов обучения искусственных нейронных сетей на кластерных вычислительных системах / О.В. Крючин, А.А. Аразмасцев // Вестн. Тамб. ун-та. Сер. Естеств. и техн. науки. 2010. — Т. 15, Вып. 6 — С. 372-375.