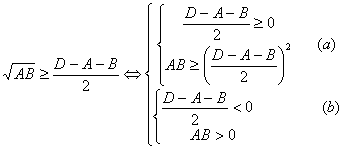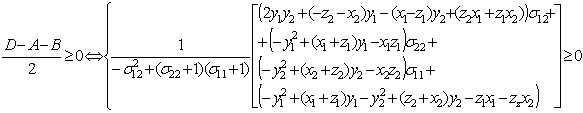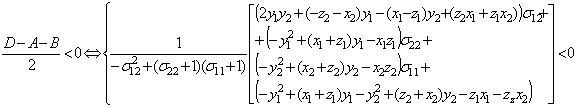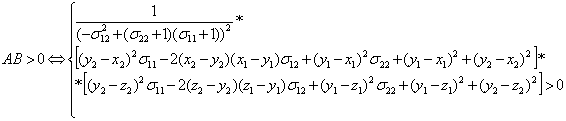Математика/4.Прикладная
математика.
К.ф.-м.н. Хачумов М.В.
Федеральное государственное бюджетное учреждение науки
Институт системного анализа Российской академии наук, Россия
Метрики в задаче
кластерного анализа, основанные на функции Махаланобиса
В задаче
кластерного анализа слабоструктурированных данных часто используются
расстояния, основанные на функции Махаланобиса [1], с помощью которых можно
определять сходство классов. Они отличаются от расстояния Евклида тем, что
учитывают дисперсии признаков и инвариантны к масштабу. В частности, к ним
относятся статистическое расстояние Махаланобиса 
, полиномиальное расстояние
Махаланобиса 
[1] и расстояние Евклида—Махаланобиса 
[2]. Функцию, предложенную Махаланобисом, традиционно называют
метрикой, что не достаточно очевидно и требует дополнительного исследования [3,4].
Пусть
задано произвольное подмножество 
Функция 
называется
расстоянием, если она удовлетворяет следующим условиям:
1) неотрицательность: 
для всех 
;
2) идентичность: 
, если и только если 
;
3) симметричность: 
для всех 
.
Расстояние
называется метрикой,
если выполняется следующее дополнительное условие:
4) неравенство
треугольника: 
для всех 
.
Рассмотрим функцию Махаланобиса
. Если матрица ковариации 
в функции 
является единичной
матрицей, то расстояние Махаланобиса становится равным расстоянию Евклида. Свойства
метрики 1)−3) выполняются для расстояний 
и 
при любом значении 
. Следует проверить и справедливость свойства 4), которое
задает правило треугольника.
Пусть 
. В этом случае имеем матрицу первого порядка, определителем
которой является элемент: 
. Тогда: 
, т.е. матрица ковариаций
и обратная ей матрица содержат по одному элементу. Для трех точек 
,
и 
следует проверить
выполнение неравенства:
|
|
(1) |
+
.Выполнив сокращение всех членов (1) на величину 
при 
получим условие 4)
неравенства треугольника, которое выполняется.
Пусть 
. Тогда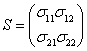 
, 
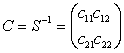, причем 
симметрическая матрица, т.е. 
. Матрица 
обратная
симметрической матрице 
также является
симметрической, поэтому далее полагаем, что: 
. Вычисление обратной матрицы приводит к следующим
соотношениям:
, 
, 
, 
, 
, где 
- дополнительный минор элемента 
матрицы 
. С учетом симметричности
матрицы 
можно записать:
,
, 
, 
.
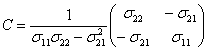Рассмотрим
три точки 
, 
, 
. Для того, чтобы функция 
была метрикой следует
доказать, что
|
|
(2) |
+
.Обозначим c целью упрощения:
, 
, 
. Откуда после возведения в квадрат: 
. Данное неравенство раскрывается следующим образом:
|
|
(3) |
Для
случая a)
Заметим
что 
в силу особенностей
матрицы ковариации. Перейдя к переменным исходной матрицы 
, получим соотношения:
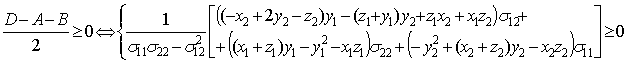
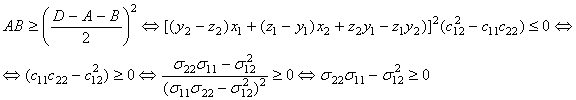
Для
случая b)
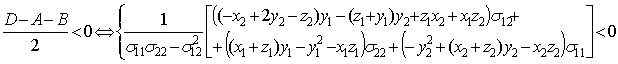
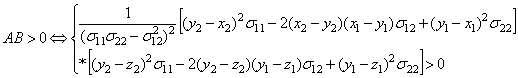
Таким образом, условие
4) для функции 
может быть выполнено
только в случае, когда для матрицы 
справедливо
неравенство (3). Вычисление левой части неравенства (3) соответствует
вычислению определителя матрицы ковариаций 
, для которой известно, что она положительно определена и ее
определитель положителен. Т.е. для 
функция 
является метрикой. В
частном же случае при 
имеем условие
неравенства треугольника в виде 
, которое всегда
выполняется.
Рассмотрим
функцию 
. Функция 
отвечает требованиям
метрики для 
. Можно показать, что добавление к матрице ковариаций 
диагональной матрицы
вида: 
приводит для 
к следующему условию
выполнения неравенства треугольника:
|
Для случая a)
|
(4) |
Для случая b)
|
|
(5) |
Полученные соотношения (4)-(5) накладывает ограничения
на вид матрицы 
.
Для 
получение условий
того, что функции 
и 
являются метриками на
основе приведенных рассуждений приводят к громоздким выражениям, что требует
поиска других, более общих, принципов построения доказательства. Доказательство
того, что 
является метрикой для
любого 
выполнено в
диссертации [3] (Ackerman M.R., 2009). Это
доказательство служит основой для доказательства по аналогии и свойств функции 
До сих пор мы рассматривали расстояние
между двумя точками одного класса, т.е. внутриклассовое расстояние. Для решения
задач классификации и кластеризации необходимо иметь инструмент для измерения
расстояний между классами и расстояний между точкой (представляющей
единственный объект множества) и классом. Чтобы
использовать расстояние Махаланобиса необходимо, в общем случае, найти матрицы
ковариаций всех классов на основе известных выборок. Затем с помощью подсчета
расстояний от заданной точки до каждого класса выбрать класс, для которого
расстояние минимально.
Покажем, при каких условиях метрика Махаланобиса может
быть использована для классификации (т.е. для определения принадлежности точки
одному из нескольких классов). Пусть заданы три класса 
в метрическом
пространстве 
Выпишем условия для
метрик, ориентированных на измерение межклассовых расстояний:
1) 
2) 
(6)
3) 
4) 
Так
как в задачах кластерного анализа импликация 2) в условиях (6), вообще говоря,
не выполняется, вводится понятие квазиметрики,
для которой выполняются следующие условия:
1) 
2)
(7)
3) 
4) 
Для
расчета расстояния между точкой 
и классом 
можно воспользоваться
расстоянием Махаланобиса 
или Евклида-Махаланобиса
. При этом второй точкой служит центр класса 
, представленный вектором средних значений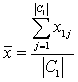 
, где 
- мощность класса, 
- элемент класса 
. Пусть точку 
надо отнести к одному
из двух классов 
, а также измерить расстояния между классами. Построим
матрицы ковариаций 
классов 
соответственно.
Объединенная матрица ковариаций для классов 
может быть задана как
сумма 
(есть и другой способ
объединения матриц ковариаций, например, 
- число элементов класса 
), а для классов 
соответственно
─ 
Расстояние 
удовлетворяет, так
же, как и расстояние Евклида, условиям: 
и является
симметричным.
Теорема. Расстояния 
являются
квазиметриками [4].
Для
доказательства теоремы достаточно показать, что
Доказательство:
Пусть 
есть симметрическая
положительно определенная матрица,
тогда существует такая несингулярная матрица 
, что 
(следует из
существования разложения Холецкого).
|
|
|
|
|
|
|
|
,
откуда получаем:
|
|
|
|
|
|
Теорема доказана.
Таким
образом, объединение частных матриц ковариаций обеспечивает выполнение свойств
квазиметрики для функций Махаланобиса (а также Евклида-Махаланобиса) в случае
измерения межклассовых расстояний. Чтобы использовать рассмотренные метрики в
задачах классификации и кластеризации необходимо найти матрицы ковариаций всех
классов на основе известных выборок. Затем с помощью подсчета расстояний от
заданной точки до каждого класса выбрать класс, для которого расстояние
минимально. Преимущество в практическом использовании имеет метрика
Евклида-Махаланобиса, которая обладает большей универсальностью.
Работа выполнена при поддержке проекта Программы
фундаментальных исследований ОНИТ РАН № 1 «Развитие методов интеллектуального
анализа данных и управления робототехническими системами с применением
бесконтактных человеко-машинных интерфейсов» и проекта РФФИ № 14-07-31020 мол_а
«Разработка и исследование математического и программного обеспечения
многофункциональных бортовых систем машинного зрения летательных аппаратов на
основе технологий анализа видеоданных и методов интеллектуального управления».
Список литературы
1. Greg Grudic and
Jane Mulligan, Outdoor Path Labeling Using Polynomial Mahalanobis Distance,
Robotics: Science and Systems II, 2006. – http://www.roboticsproceedings.org/rss02/p20.pdf
2.
Амелькин С.А., Захаров
А.В., Хачумов В.М. Обобщенное расстояние Евклида-Махаланобиса и его свойства. –
Информационные технологии и вычислительные системы, № 4, 2006, с. 40-44.
3. Ackerman M.R.
Algorithms for the Bregman k-Median Problem. – A dissertation submitted to the
Department of Computer Science University of Paderborn, 2009.–220 p.
4.
Хачумов М.В. Расстояния,
метрики и кластерный анализ. – Искусственный интеллект и принятие решений, № 1,
2012, с. 81-89.