Кудайкулов А.А.

Казахский Национальный Университет имени аль-Фараби, Казахстан

Прямое численное моделирование течения однофазной жидкости в пористой среде с периодической микроструктурой

В работе представлены результаты математического и численного моделирования течения однофазной жидкости в пористой среде с периодической микроструктурой, на основе уравнений Навье - Стокса для несжимаемой жидкости:

, (1)

, (2)

где – плотность жидкости, – скорость течения жидкости, – давление, – вязкость жидкости и – ускорение свободного падения. Основная сложность моделирования течения жидкости в пористой среде, на основе уравнений Навье-Стокса, заключается в том, что очень тяжело корректно поставить граничные и начальные условия для системы уравнений (1) и (2). В статье [2] доказывается, что при нулевом начальном условии для скорости и периодическом граничном условии для скорости и давления, система уравнений (1) и (2) имеет решение и оно единственно, а также непрерывно зависит от этих условий. В случае, если необходимо задать более сложные граничные и начальные условия для скорости и давления, то можно измерить эти значения экспериментальным путем [5,6]. В данной работе рассматривается нулевое начальное условие для скорости и периодическое граничное условие для скорости и давления. Аналитическое решение системы уравнений (2) и (4) найдено только для частных случаев и для простых областей. Поэтому для решения системы уравнений (2) и (4) применяются численные методы. В данной работе применяется метод контрольного объема с адаптивным измельчением сетки [7, 8, 9].

В работе рассматривается двумерная прямоугольная область размером (где меняется от до и меняется от до ), в которой периодическим образом расположены цилиндры (рис. 1). Начальное условие для скорости задается следующим образом:

. (5)

Граничные условия для скорости и давления имеют следующий вид:

1) На границах области:

,

, (6)

,

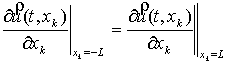2) На поверхности цилиндров (условие прилипания):

, (7)

где – количество измерений, в нашем случае .

Для нахождения скорости фильтрации – , необходимо усреднить значение скорости по объему:

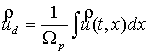, (8)

где – объем порового пространства. Далее из закона Дарси [1,4] можно найти проницаемость пористой среды:

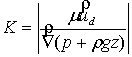(9)

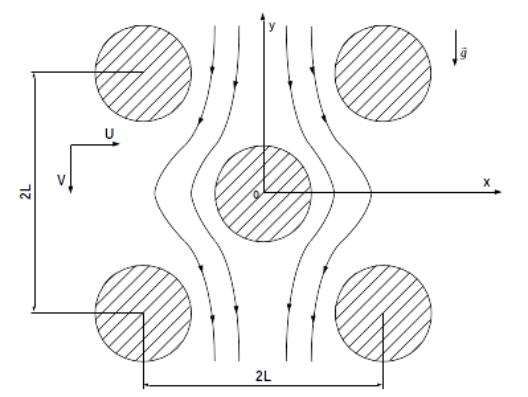
Рис. 1 Двумерная прямоугольная область размером (где меняется от до и меняется от до ), в которой периодическим образом расположены цилиндры

Литература

1. Баренблатт Г.И., Ентов В.М., Рыжик В.М. Движение жидкостей и газов в природных пластах, Москва, Недра, Россия, 1984, 211 с.

2. Отелбаев М. Существование сильного решения уравнения Навье - Стокса, Математический журнал, том 13, №4(50), стр. 5 - 104, 2013.

3. Прохоров А.М. Большая физическая энциклопедия, Москва, Советская энциклопедия, Россия, 1988, в 5 томах.

4. Bear J., Cheng A.H.-D. Modeling Groundwater Flow and Contaminant Transport, Theory and Applications of Transport in Porous Media, Springer, Volume 23, 2010.

5. Karadimitriou N.K. Two-phase flow experimental studies in micro-models, Utrecht, Netherland, 2013.

6. Li D. Encyclopedia of Microfluidics and Nanofluidics, Springer, 2008.

7. Louis H. H., John B. B. An Adaptive Mesh Projection Method for Viscous Incompressible Flow, SIAM Journal on Scientific Computing 18(4):996-1013, 1997.

8. Popinet S. Gerris: a tree-based adaptive solver for the incompressible Euler equations in complex geometries, Journal of Computational Physics 190(2):572-600, 2003.

9. Sidilkover D., Ascher U. M. A Multigrid Solver for the Steady State Navier-Stokes Equations Using The Pressure-Poisson Formulation, Comp. Appl. Math 14:21-35, 1995.