Òåîðåòè÷åñêàÿ ôèçèêà
Fractals features of the atomic nuclei
D. K.
Ershov
Physics
Departament, Smolensk State University,
Smolensk,
Russia
Email: ershov-smolgu@yandex.ru
ABSTRACT
Have
been calculated of the exponents Gelders
/ Herst/ α, β, γ: ΔZ=(ΔN)α, Δ Z =(Δ A) γ, Δ N = (Δ A) β ,
which is connected Δ Z, Δ N and ΔA in
chains
of the even ΔZ families of stable isotopes. Are observed periodical occurrence of
the sets of values (α, β, γ). This is clear illustration of the fractals feature
of the nuclear structures.
Keywords:
stable isotopes, Gelders exponents, fractals, multifractals.
Atomic
nuclei even relatively light elements are complex systems consisting of
nucleons with many degrees of freedom and participating in different
interactions [1] .
Unified
strict theory of such systems is still not built, so it seems reasonable use of
the phenomenological approaches to the study of various properties of atomic
nuclei.
In
modern physics is actively and successfully uses the methods of fractal
analysis of various systems [2-4].
In this
paper we study the fractal properties of the nuclei of stable isotopes of
elements.
Connection
between the number of neutrons (N) and protons (Z) in the nuclei of stable
isotopes has a nonlocal nature of the nuclei of one element (![]() ) have several isotopes (
) have several isotopes (![]() ), and kernel - isotones with the given number of neutrons (
), and kernel - isotones with the given number of neutrons (![]() ) may be owned by different elements (
) may be owned by different elements (![]() ).
).
Nonlocality
of mathematically reflected in the fractional value exponents Gelders [5,6]. It
is almost evident, for example, if x<<1:
![]() , (1)
, (1)
while
![]() (endless series). (2)
(endless series). (2)
Therefore
integer derivatives are local values, and the fractional - nonlocal (integral),
i.e. not defined in point, and only in a variable values region.
Accordingly,
on the plane (Z, N) has a region of stability, not a line graph stability.
In this
paper we calculate the indicators holder Gelders (Herst) (![]() ):
):
![]() , (3)
, (3)
![]() , (4)
, (4)
![]() . (5)
. (5)
Where ![]() - the change in the number of neutrons, Δ Z - number of protons, ∆ A- change the mass
number (A = N + Z).
- the change in the number of neutrons, Δ Z - number of protons, ∆ A- change the mass
number (A = N + Z).
We consider
consistently neighboring even-Z values, because only even the charge on the
nucleus have several stable isotopes.
And for
those of neighbouring even nuclei, we compare the most light isotopes from ![]() and most heavy - with
and most heavy - with
![]() :
:
![]() (6)
(6)
![]() (7)
(7)
![]() (8)
(8)
![]() (9)
(9)
Δ Z = 2 (all compared pairs of
adjacent elements).
It is
easy to show that
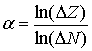 (10)
(10)
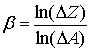 (11)
(11)
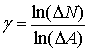 (12)
(12)
It is
easy to see that ![]() , but for completeness, we give the values of all three
indices.
, but for completeness, we give the values of all three
indices.
For
each pair of adjacent elements we have two sets of values (max and min).
We
begin with neon ![]() , settings
, settings ![]() , which determine the oxygen-
, which determine the oxygen-![]() and end lead
and end lead ![]() . We use data [7, 8].
. We use data [7, 8].
Just
have 36x2 = 72 set of values ![]() .
.
Quite
surprising that there are only 4 different set of values : ( 1.0, 0.5, 0.5 ); (
0.5, 0.774, 0.387); ( 0.387, 0.861, 0.333 ); ( ∞, 1.0, ∞).
Moreover,
the uncertainty ∞ are available in 5 cases, and they correspond to the
magical N cores ![]() .
.
Another
( the only hand ) anomaly ( 1.0 , 0.387, 0.387 ) was observed in the magic
nucleus ![]() , i.e. magical N kernel stable isotopes match a kind of
“critical” nuclei.
, i.e. magical N kernel stable isotopes match a kind of
“critical” nuclei.
The
magic number N = 126 in a stable region to show themselves not “time”.
Sequential
sets of values (![]() ) means something like self-similarity of nuclear structures,
i.e. fractal nature of nuclei (more precisely - multifractal) [9].
) means something like self-similarity of nuclear structures,
i.e. fractal nature of nuclei (more precisely - multifractal) [9].
Recently
extensively studied cluster models of atomic nuclei [10, 11].
The
clustering properties of nuclei, apparently, also characterize the fractal
nature of cores, but, perhaps, in a somewhat different aspect.
It is
known that the definition of fractals and fractal dimensions, allows a certain
variability [12].
Summing
up, we can say that the structure of the nuclei of stable isotopes of elements
demonstrates multifractal nature. The phenomenon of scaling /self-similarity, fractal
/ long been well known in the physics of high energies / z - scaling / [12].
As you
can see, this manifests itself in nuclear physics medium energies. Perhaps the
main role is played not the value of the energy, and the intensity of the
interaction constant of the strong interaction.
REFERENCES.
1. Y.P.
Gangrsky, I. Zhemenik. B.N. Markov, V. Mishinskiy. Relations outputs isotopes
of iodine and xenon in the photofission fragments of heavy nuclei. Preprint
JINR. P15-2010-16.
2. E.
Federer. Fractals. M World. 1991.[J. Federer/ Fractals. New. York and London:
Plenum Press, 1988]
3. B.
Mandelbrot. The fractal geometry of nature. M. 2002. [B. Mandelbrot. The
Fractal Geometry of Nature. Freeman. San Francisco. 1982]
4. B.M.
Smirnov. Physics of fractal clusters. M. Science. 1991. ñ.135.
5. R.T
Sabitov, V.V. Uchaikin. Fractional differential approach to the description of
the dispersion transfer in a semiconductor. Phys. ò.179 no.10. 2009. C. 1079-1104.
6. A.
M. Nachuschev. Fractional calculus and its application. M. Fizmatlit. 2003.
p.272.
7.
Physical quantities. Handbook. M. Energoatomizdat. 1991. ñ.1232.
8. J. Emsly.
The elements. M World. 1993. ñ.256. [J. Kasper.
The Elements. Clarendon Press. Oxford. 1991.]
9. A.N.
Pavlov, V.S. Anishchenko. Multifractal analysis of complex signals. Phys. ò.177, ¹8, 2007. ñ.859-876.
10. M.
Freer. The clustered nucleus-cluster structures in stable and unstable nuclei.
Rep. Prog. Phys. 2007. v.70. p.2149-2210.
11.
P.I. Zarubin. Peripheral fragmentation of relativistic nuclei. Preprint JINR.
P1-2010-75.
12. T.
G. Dedovich, Tokarev M.V.. Method of p-adic coatings for fractal analysis of
showers. Preprint JINR. P2-2011-3.