Физика/1. Теоретическая физика.

К.ф.-м. н. Севрюков П. Ф.

Ставропольский государственный педагогический институт, Россия

О дополнительных аналитических первых интегралах задачи о движении спутника трёхосной планеты.

Рассмотрим задачу о движении спутника, принимаемого за материальную точку, в поле тяготения равномерно вращающейся трёхосной планеты.

Гравитационный потенциал планеты во внешней точке с координатами r, φ λ в стандартных обозначениях может быть представлен формулой

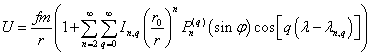(1)

где f – гравитационная постоянная, т и r₀ – масса и средний экваториальный радиус планеты соответственно, - присоединённая функция Лежандра, безразмерные коэффициенты и характеризуют распределение масс внутри планеты и её фигуру.

Гравитационный потенциал планеты может быть представлен в виде суммы аппроксимирующего потенциала W и пертурбационной функции R;

U=W+R. (2)

В качестве аппроксимирующего потенциала W выберем потенциал обобщённой задачи двух неподвижных центров [1,2]. Этот потенциал (его ещё называют потенциалом эйлеровой задачи) W включает в себя вторую и третью полностью, а остальные зональные гармоники гравитационного потенциала частично. Члены потенциала (1), не вошедшие в W, составят пертурбационную функцию.

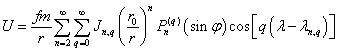, (3)

где для зональных гармоник J_n,q = j_n, а для секториальных и тессеральных J_n,q = I_n,q; параметры j_n представляют собой части J_n,0, не учтённые аппроксимирующим потенциалом.

Уравнения движения невозмущённой эйлеровой задачи интегрируются в квадратурах. Е.П. Аксёновым [1] введены различные системы канонических элементов для этой задачи. Дифференциальные уравнения возмущённой эйлеровой задачи принимают наиболее простую форму, если ввести канонические переменные L, G, H, l, g, h, подобные элементам Делоне [2]. Уравнения возмущённого движения в канонических оскулирующих элементах L, G, H, l, g, h будут иметь вид

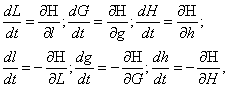(4)

причём

. (5)

Ясно, что в формуле (5) - невозмущённый гамильтониан эйлеровой задачи, R - пертурбационная функция.

Невозмущённый гамильтониан Н₀ запишется как

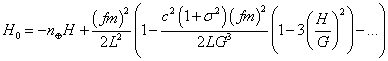…………(6)

В формуле (6) с и σ – вещественные постоянные эйлеровой задачи, - абсолютная скорость вращения планеты.

Воспользуемся известными в теории движения искусственных спутников функциями наклона и эксцентриситета [1]. Функции эксцентриситета выразятся через коэффициенты Ганзена

. (7)

Функции наклона зададим в виде

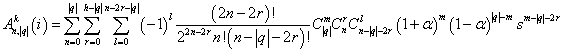, (8)

где α = cosi, s = sini, h = или h = , смотря по тому, чётное, или нечётное п.

Если a, e, i, ω₀, M, Ω – элементы эйлеровой орбиты, являющиеся аналогами большой полуоси, эксцентриситета, наклона, аргумента перицентра, средней аномалии, долгота восходящего узла кеплеровской орбиты, а S – звёздное время, то пертурбационная функция может быть записана следующим образом:

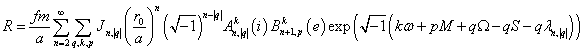(9)

Громоздкие формулы связи между каноническими элементами и элементами эйлеровой орбиты дают возможность получить разложение пертурбационной функции в кратный ряд Фурье по угловым переменным:

, (10)

а затем представить функцию R рядом

, (11)

где μ = r₀c^-110^-8, а Н₀ выражается формулой

. (12)

Движение спутника трёхосной планеты описывается системой уравнений (4), при этом гамильтониан задачи задаётся как

(13)

Для рассматриваемой задачи справедлива теорема Пуанкаре [3]:

- пусть движение спутника описывается системой (4), причём гамильтониан имеет вид (13), тогда если функция H₀ не зависит от угловых переменных l, g, h, гессиан функции H₀ по переменным L, G, H не равен тождественно нулю, функции H_i являются периодическими функциями от l, g, h с периодом 2π, то я система не допускает никаких других независимых аналитических первых интегралов, кроме интеграла Якоби H=сonst при достаточной малости параметра μ.

Нетрудно проверить, что все условия сформулированной теоремы выполняются. В формулировке отсутствует упоминание о том, что в разложении пертурбационной функции в кратный ряд Фурье по угловым переменным коэффициентов, которые не обращаются в нуль, становится вековым, должно существовать бесконечное множество. Однако в доказательстве теоремы учтён этот факт.

Итак, при аппроксимации гравитационного потенциала трёхосной планеты потенциалом обобщённой задачи двух неподвижных центров задача о возмущённом движении спутника трёхосной, равномерно вращающейся планеты не имеет при достаточной малости параметра дополнительного аналитического аналитического первого интеграла, не являющегося следствием интеграла Якоби.

Ранее задача о движении материальной точки в поле тяготения равномерно вращающегося твёрдого тела с трёхосным центральным эллипсоидом инерции рассматривалась А.Х. Борхамом [4]. Им доказано, что уравнения возмущённого движения материальной точки не могут иметь дополнительного однозначного аналитического первого интеграла, не являющегося следствием интеграла Якоби. В качестве невозмущённой задачи Борхамом выбрана задача двух тел.

Литература.

1. Аксёнов Е.П. Теория движения искусственных спутников Земли. М.: Наука. 1977. 360 с.

2. Дёмин В.Г. Движение искусственного спутника Земли в нецентральном поле тяготения. М.: Наука, 1968. 352 с.

3. Пуанкаре А. Новые методы небесной механики. Т, 1//Пуанкаре А. Избр. Труды Т. 1. М.: Наука, С 8-326.

4. Borham A.H. About the non-existence of additional analytical integral in the problem of satellite’s motion under the gravitational attraction of a triaxial rigid body./ Celect. Mech., 1983, v.29, №4, p. 323-328.