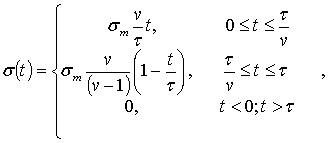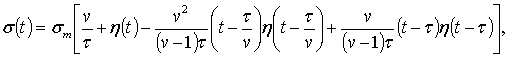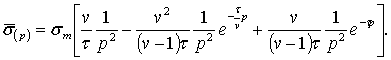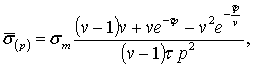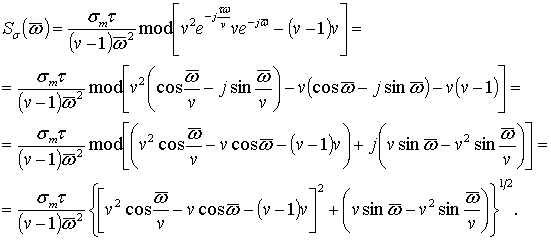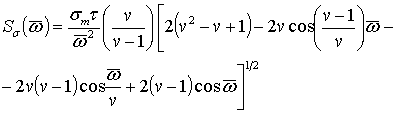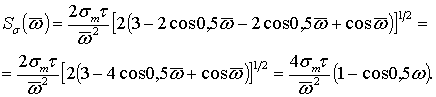Докт. техн. наук, професор Нагорний В.П., канд. техн. наук Денисюк І.І.

Інститут геофізики ім. С.І. Субботіна НАН України

Швейкіна Т.А.

Український науково-дослідний інститут природних газів

ПАРАМЕТРИ ІМПУЛЬСНОГО НАВАНТАЖЕННЯ І ПЕРЕНЕСЕННЯ ЕНЕРГІЇ В СЕРЕДОВИЩІ ПЛАСТА

Питанню зміни параметрів імпульсного навантаження при його розповсюдженні в гірському масиві присвячені роботи [1, 2]. Встановлено, що імпульс низької амплітуди сприяє більш рівномірному розподілу енергії в гірському масиві і більш рівномірному його дробінню [3]. Відомо також, що форма імпульсу спотворюється в процесі розповсюдження його по гірському масиву, оскільки різні частотні складові імпульсного навантаження розповсюджуються по гірському масиву з різною швидкістю [1].

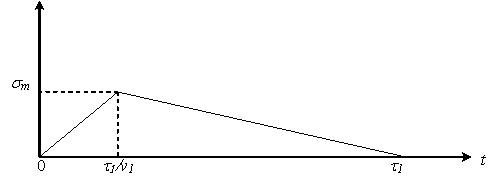
Розглянемо вплив швидкості імпульсного навантаження та тривалості розвантаження на спектральні характеристики приймаючи, що імпульсне навантаження моделюється імпульсом трикутної форми (рис. 1). Такий імпульс описується залежністю:

(1)

де – максимальне значення імпульсного навантаження; – тривалість імпульсної дії; – час наростання імпульсного навантаження до максимального значення ( – довільне число більше одиниці).

Для побудови амплітудно-частотного спектру функції (1) знайдемо її зображення по Лапласу, в подальшому від знайденого зображення перейдемо до амплітудно-частотного спектру.

Рис. 1. Імпульс трикутної форми тривалістю

Користуючись узагальненою одиничною функцією, оригінал можна представити у вигляді:

(2)

де – узагальнена одинична функція:

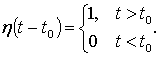
Зображення Лапласа функції (2) згідно [4] має вигляд:

(3)

Після спрощень вираз (3) запишеться:

(4)

де – комплексний параметр.

Для знаходження амплітудно-частотного спектру імпульсної дії (2) покладемо і знайдемо модуль комплексної величини :

(5)

У виразі (5) введемо безрозмірну кругову частоту , в результаті одержимо

(6)

Після алгебраїчних перетворень вираз (6) набуває вигляду:

(7)

При (імпульс має форму рівнобедреного трикутника) із (7) після спрощень одержимо

(8)

Вираз (8) співпадає з одержаним в роботі [4] амплітудно-частотним спектром для імпульсу в формі рівнобедреного трикутника.

З використанням залежності (7) дослідимо амплітудно-частотний спектр імпульсу трикутної форми в залежності від параметра , що характеризує швидкість імпульсного навантаження. Результати досліджень приведені в табл. 1 та на рис. 2.

Таблиця 1

Результати розрахунків амплітудно-частотного спектра при зміні швидкості імпульсного навантаження

Безрозмірна частота	Амплітуда частотного спектра при різних значеннях параметра
	= 2	= 100	= 500
0	1	1	1
1	0,980	0,968	0,943
2	0,920	0,894	0,891
3	0,826	0,776	0,773
4	0,708	0,632	0,629
5	0,576	0,484	0,480
6	0,442	0,352	0,349
8	0,206	0,222	0,222
10	0,057	0,214	0,214
12	0,002	0,175	0,174
14	0,010	0,133	0,133
16	0,036	0,128	0,128
18	0,047	0,116	0,116
20	0,036	0,096	0,095
22	0,016	0,091	0,091
24	0,002	0,087	0,086
26	0,001	0,075	0,074

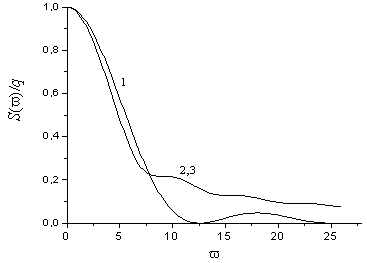
Рис. 2. Спектри імпульсів при різних значеннях параметра :

1,2,3 – =2; 100; 500, відповідно

Розрахунки виконувались за формулами:

при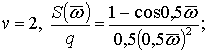

при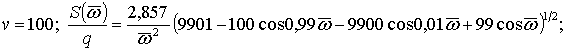

при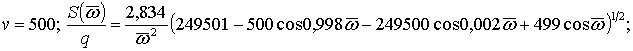

де – величина імпульсу трикутної форми.

Аналіз даних табл. 1 та рис. 2 показує, що при малому часі наростання максимального значення імпульсу спектр зсувається в область більш високих частот. А так, як високі частоти при проходженні по гірській породі затухають значно швидше, ніж низькі [1], для перенесення енергії імпульсного навантаження в геофізичному середовищі на більш значні відстані необхідно, щоб початковий імпульс мав в своєму складі більше низьких частот, що досягається зменшенням крутизни наростання початкового імпульсу. Відмічений факт може бути використаний для створення такої імпульсної дії на породи-колектори, що дозволить підвищити ефективність обробки масиву у привибійній зоні продуктивного пласта, що позитивно вплине на дебіт видобувної свердловини.

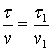Розглянемо вплив розвантаження при імпульсній дії на гірський масив при постійній швидкості навантаження (час наростання імпульсної дії до максимуму однаковий) на амплітудно-частотний спектр. На рис. 3 зображений модельний імпульс, тривалість дії якого , що перевищує на рис. 1. Із умови знаходимо параметр (при умові, що – відомі).

Рис. 3. Імпульс трикутної форми тривалістю

Таблиця 2

Результати розрахунків амплітудно-частотних спектрів при зміні тривалості процесу розвантаження і незмінній швидкості навантаження

Безрозмірна частота	Амплітуда частотного спектра при різних значеннях параметрів і
	= 100 мс; = 500	= 160 мс; =800
0	1	1
1	0,943	0,987
2	0,891	0,895
3	0,773	0,774
4	0,629	0,629
Продовження табл. 2
5	0,480	0,480
6	0,349	0,348
8	0,222	0,222
10	0,214	0,214
12	0,174	0,174
14	0,133	0,133
16	0,128	0,128
18	0,116	0,116
20	0,095	0,095
22	0,091	0,091
24	0,086	0,086
26	0,075	0,075

В табл. 2 приведені результати обчислень амплітудно-частотних спектрів для імпульсів з різним часом розвантаження: тривалість першого імпульсу , тривалість другого імпульсу . Із аналізу даних табл. 2 очевидно, що час розвантаження майже не впливає на частотний склад імпульсів. Різниця помітна лише на частотах .

Таким чином, відповідальною за передачу енергії імпульсної дії у віддалені від джерела навантаження точки гірського масиву є крутість наростання імпульсної дії до максимального значення, в той час як тривалість процесу розвантаження на спектральні характеристики імпульсу впливає незначно.

Література:

1. Друкованый М.Ф., Комир В.М., Кузнецов В.М. Действие взрыва в горных породах. – Киев: Наук. думка, 1973. – 184 с.

2. Основы теории и методы взрывного дробления горных пород / Э.И. Ефремов, В.С. Кравцов, Н.И. Мячина и др. – К.: Наук. думка, 1979. – 224 с.

3. Казаков Н.Н. Взрывная отбойка руд скважинными зарядами. – М.: Недра, 1975. – 192 с.

4. Харкевич А.А. Спектры и анализ. – М.: Физматгиз, 1962. – 236 с.