Л.М. Буниатян, А.Т. Уликян, Д.У. Егиазарян, М.А. Чтчян

Государственный инженерный университет Армении, г. Ереван

СИСТЕМА УПРАВЛЕНИЯ ИСКУССТВЕННОЙ РУКИ НА ОСНОВЕ

ГЛОБАЛЬНОГО КОМПЕНСАТОРА

Роботизированные системы медицинского и других назначений относятся к многомерным системам автоматического регулирования. Они характеризуются сложными нелинейными характеристиками и законами управления, а также особыми требованиями к динамической точности, безопасности и надежности [1]. Поэтому применение современных методов теории систем управления и разработка новых эффективных методов исследования и проектирования робототехнических устройств и систем в сфере медицинских приложений является важной и сложной задачей.

В работе рассматривается система управления искусственной руки (ИР) с шестью степенями свободы, динамика которой описывается сложными нелинейными взаимосвязанными уравнениями. Предлагается подход к системе управления ИР, основанный на применении известного в робототехники метода обратной динамики [2]. Это позволяет существенно упростить практическую реализацию системы, с сохранением качественных характеристик в приемлемых границах.

Уравнения движения ИР в общем виде записываются в следующей векторной форме:

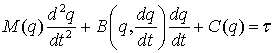, (1)

где есть N - мерный вектор обобщенных координат (угловых вращений) с компонентами ; - симметричная положительно-определенная матрица моментов инерции; - матрица центробежных и Кориолисовых ускорений; - вектор гравитационных сил; - вектор приложенных внешних моментов [2].

В качестве конкретного примера рассмотрена математическая модель антропоморфического робота-манипулятора, нелинейные уравнения движения и численные значения параметров которого даны в [3]. На основании теоретических результатов в работах [4, 5] получены частотные и корневые характеристики и требуемый глобальный компенсатор системы управления ИР с шестью степенью свободы. Вычисление глобального компенсатора осуществлялось с помощью соответствующей программы на языке MATLAB на основе линеаризации нелинейных уравнений движения в различных точках пространства состояний системы и выбора “наихудших” рабочих точек [5]. В этом смысле глобальный компенсатор гарантирует удовлетворение требуемых частотных критериев качества системы на всем пространстве состояний. Это позволяет существенно упростить процедуру практической реализации системы, поскольку здесь отсутствует необходимость использзования так называемого метода планирования коэффициентов усиления (Gain Scheduling).

Расчеты дали следующую передаточную функцию глобального компенсатора:

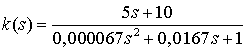. (2)

Анализ устойчивости системы управления ИР проведен при помощи обобщенного критерия Найквиста. Частотные характеристики системы управления ИР без использования и с использованием глобального компенсатора (2) изображены на рис. 1 и рис. 2, откуда видно, что нескорректированная система неустойчива (рис. 1), а при применении глобального компенсатора (1) замкнутая система устойчива (рис. 2).

Чтобы обосновать правомочность применения глобального компенсатора к линеаризованным уравнениям движения ИР, а также для исследования динамики спроектированной системы управления, с помощью пакета Simulink была разработана нелинейная модель системы. На рис. 3 приведена блок-схема нелинейной модели системы управления ИР с шестью степенью свободы.

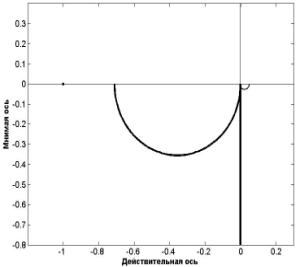
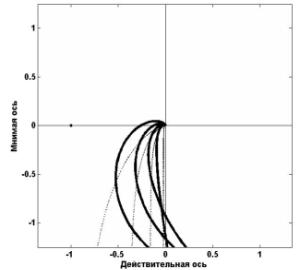
Рис. 1. Диаграммы Найквиста Рис. 2. Частотные характеристики системы исходной системы. с использованием глобального компенсатора.

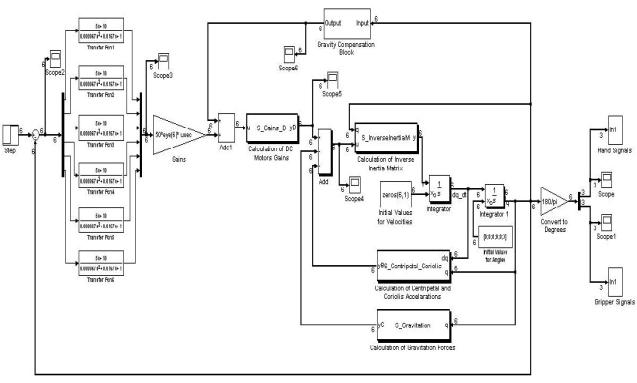
Рис. 3. Нелинейная модель системы управления искусственной

верхней конечности с шестью степенью свободы.

На рис. 4 даны графики изменения сигналов ошибки нелинейной модели системы управления ИР с глобальным компенсатором (2), откуда видно, что динамические процессы в системе имеют приемлемые качественные характеристики.

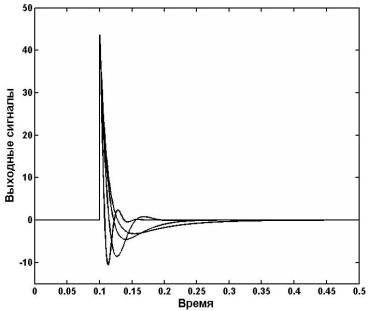
Рис. 4. Графики изменения сигналов ошибки нелинейной модели с

использованием глобального компенсатора

СПИСОК ЛИТЕРАТУРЫ

1. Gasparyan O.N. Linear and Nonlinear Multivariable Feedback Control: A Classical Approach. - John Wiley & Sons, UK, 2008. - 356 p.

2. Spong M., Hutchinson S., Vidyasagar M. Robot Modeling and Control. - Wiley, Hoboken, NJ 2006. - 419 p.

3. Armstrong B., Khatib O. and Burdick J. The explicit dynamic model and inertial parameters of the PUMA 560 arm // Proc. 1986 IEEE Conf. Robot. Autom. - San Francisco, Apr. 7–10, 1986. – P. 510–518.

4. Гаспарян О.Н., Буниатян Л.М. О линеаризации уравнений движения искусственной руки с учетом динамики исполнительных двигателей // Информационные Технологии и Управление, 2011, № 3, с. 280-287.

5. Гаспарян О.Н., Егиазарян Г.Г., Буниатян Л.М. Проектирование системы управления искусственной руки методом характеристических передаточных функций // Информационные Технологии и Управление, 2011, № 4, с. 15-22.