Алюков А.С.

Южно-Уральский государственный университет, Челябинск, Россия

Построение системы управления робототехнической колесной платформой

Новое поколение робототехнических систем характеризуется повышенной мобильностью, активным взаимодействием с внешней средой, расширенными способностями приспособления к сложному, неопределенному и подвижному окружению. Высокие качественные характеристики и подвижность так называемых активных роботов используется для выполнения целого ряда нетривиальных операций, таких как обход препятствий, проникновение в труднодоступные зоны, выбор удачного подхода к внешним объектам и прецизионное движение по сложным криволинейным трассам с сохранением требуемой ориентации в пространству. Мобильность активных роботов, приспосабливаемость к внешней среде и сравнительная автономность делает их использование весьма привлекательным для самых разнообразных сфер человеческой деятельность, включая автоматизированное производство, космос и подводные исследования, оборону, медицину и т.д.

Основной задачей подвижных роботов является так называемая траекторная задача – перемещение в рабочем пространстве по предписанной траектории (трассе). Трасса может быть задана с помощью светоотражающей полосы, кабельной линии, светового луча, определена контуром внешних предметов или введена в систему управления аналитически [1]. При движении робота вдоль подвижных объектов описание трассы изменяется во времени, что порождает нестационарную задачу управления траекторным движением. При этом во всех случаях полагается, что робот оснащен адекватной измерительной системой, позволяющей определить текущее положение робота на плоскости и/или значения отклонения от заданной траектории [2]. В условиях, когда аналитическое описание заранее не известно, возникает необходимость использования специальных стратегий управления траекторным движением с использованием принципов адаптации и самообучения.

Объект управления представляет собой 4-колесную автономную платформу с 2 ведущими передними колесами. Модель платформы представлена на рис. 1. Платформа предназначена для сбора аудио- и видеоинформации. В дальнейшем также планируется оснастить платформу манипулятором.

Рис. 1. Модель колесной платформы

Главной целью работы является математическое описание и создание имитационного комплекса автономной колесной платформы, а также реализация разработанных алгоритмов управления на языке программирования высокого уровня.

Как объект управления колесная платформа является сложной существенно нелинейной динамической системой. Задача, решаемая системой управления колесной платформы, заключается в создании управляющих воздействий, обеспечивающих перемещение центра масс или другой важной точки (полюса) платформы в рабочем пространстве с учетом целого ряда ограничивающих условий, представленных в виде функциональных соотношений различных переменных системы. В траекторных задачах наиболее важные и очевидные соотношения даются аналитическим описанием заданной траектории движения (трассы) S [1].

Рассматриваемая колесная платформа имеет два ведущих колеса. Ведомые (пассивные) колеса можно исключить из рассмотрения. Схема платформы с принятыми обозначениями изображена на рис. 2.

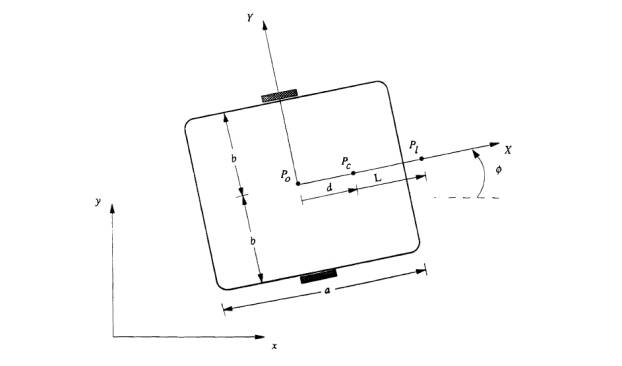
Рис. 2. Схема платформы

Здесь:

x, y – абсолютная земная система координат;

X,Y – связанная система координат;

геометрический центр платформы с координатами (;

центр масс платформы с коориднатами

референтная точка платформы с координатами ;

b – расстояние от ведущего колеса до оси симметрии;

r – радиус ведущих колес;

масса платформы без учета массы ведущих колес;

масса каждого ведущего колеса;

момент инерции платформы без учета ведущих колес относительно вертикальной оси, проходящей через центр масс;

момент инерции каждого ведущего колеса относительно оси колес;

момент инерции каждого ведущего колеса относительно диаметра колеса;

a – длина платформы;

d – расстояние по оси X от точки до точки .

Исключая из рассмотрения пассивные колеса, движение платформы описывается с помощью 5 обобщенных координат: 3 переменные описывают положение и ориентацию платформы в пространстве; 2 переменные определяют угловое положение ведущих колес.

Пусть где координаты точки центра масс в земной системе координат, φ – угол ориентации платформы (как на рис. 2); углы поворота правого и левого ведущих колес соответственно.

Полагая, что ведущие колеса катятся без проскальзывания, для системы можно записать 3 уравнения связей:

(1)

(2)

(3)

Система уравнений движения платформы состоит из 5 уравнений и имеет следующий вид [3]:

(4)

где ,

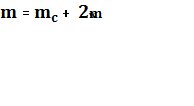моменты, создаваемые двигателями на правом и левом колесе соответственно; неопределенные множители Лагранжа.

Уравнения (1), (2), (3) можно записать в матричном виде ,

где .

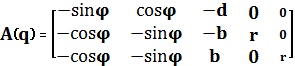Систему уравнений (4) можно записать в матричном виде

(5)

В данной записи

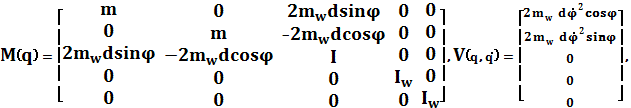
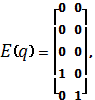
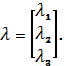
Сложность работы с уравнением (5) объясняется наличием в нем неопределенных множителей Лагранжа. В [3] показан способ избавления от данных множителей. В соответствии с ним, необходимо найти матрицу S(q), которая удовлетворяет уравнению

В данном случае матрица S(q) имеет вид

Далее, необходимо выбрать вектор, состоящий из 2 элементов , так что

(6)

Тогда, продифференцировав уравнение (6), подставив выражение для в (4) и умножив обе части (4) на , мы получаем матричное уравнение движения, не содержащее неопределенных множителей Лагранжа.

В случае рассматриваемой конструкции в качестве вектора ν можно выбрать скорости изменения углового положения левого и правого ведущих колес ν=.

В результате выполнения работы была получена система траекторного управления для автономной колесной платформы. Разработка включает в себя использование новейших методов теории нелинейного управления. Динамическая модель объекта и система управления были смоделированы в программной среде Matlab/Simulink. Моделирование показало хороший результат отработки различных заданий траектории.

Литература:

1. Бурдаков С.Ф., Мирошник И.В., Стельмаков Р.Э. Системы управления движением колесных роботов. – СПб.: Наука, 2001. – 229 с.

2. Алюков А.С. Совершенствование конструкции динамически стабилизируемых робототехнических систем на основе сферического колеса. Материалы VIII Международной научно-практической конференции "Образование и наука в XXI веке". – Том 48. Технологии. – София, Болгария: "Бял ГРАД-БГ" ООД. – 2012. – С. 64-67.

3. Nilanjan Sarka, Xiaoping Yun, R. Vijay Kumar. Control of Mechanical System with Rolling Constraints: Application To Dynamic Control of Mobile Robots. – University of Pennsylvania,1992. – 28 p.