к.т.н. Перминов Б. А.

аспирант Заикин С. Ф.

Ухтинский государственный технический университет, Россия

ИССЛЕДОВАНИЕ СТРУКТУРНОЙ МОДЕЛИ БУРИЛЬНОЙ КОЛОННЫ В ПАКЕТЕ MATH LAB

Расчёт и проектирование систем управления бурением в первую очередь определяется динамическим поведением бурильной колонны. Наиболее распространёнными событиями динамики бурильной колонны являются крутильные и продольные колебания, стопорение и проскальзывание бурового инструмента, закручивание колонны труб и возникновение биений изгибных полуволн вследствие их прижатия к стенкам скважины, изменение угловой скорости породоразрушающего инструмента в результате крутильных автоколебаний бурильной колонны в забое скважины и т.д.

Попытки определения оптимальных параметров процесса углубления скважины, при которых этот процесс определяется устойчивым режимом, предпринимались неоднократно. В частности в работах Юнина Е. К., Хегая В. К. [1,2] рассматриваются значения оптимальных параметров угловой скорости бурового инструмента и приложенного к нему давления в расчётных зонах их изменения в зависимости от глубины проходки скважины. Однако эти задачи решаются в краевых ограничениях и не предусматривают анализа колонны бурильных труб как объекта автоматического регулирования. Виртуальность такого подхода к анализу динамического поведения бурильной колонны в процессе углубления скважины не позволяет прогнозировать реальную динамику.

Для учёта всех нагрузок, воздействующих на бурильную колонну, возникает необходимость её представления ввиде цепочной структуры с распределёнными параметрами [3]. При представлении бурильной колонны в виде многомассовой структуры с упругими связями можно проследить не только передачу воздействия крутящего момента от устья скважины к забою, но и охватить эту структуру компенсационной обратной связью, которая автоматически учитывает и диссипативные силы сопротивления вращению бурильной колонны. Однако описать динамику такой структуры, содержащей n элементов практически невозможно. Поэтому в качестве реальной структуры цепи с распределёнными параметрами можно взять её двух массовый эквивалент с допущением, что одна масса сосредоточена на устье скважины, а вторая на её забойном участке. При сокращении упругих связей такое допущение справедливо.

Уравнения движения такой структуры имеют вид:

                      (1)

                       (2)

                        (3)

                                                 (4)

                                                 (5)

+           (6)

         или

                                                           (7)

Здесь С12 – коэффициент упругости; β12 – коэффициент вязкого трения.

На основании выражений 1-7 составим структурную схему двухмассовой модели. (Риc. 1).

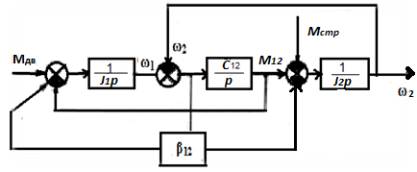
Рисунок 1 – Эквивалентная структурная схема колонны на основе двух массовой модели

Провести исследование представленной структуры оказывается затруднительным вследствие наличия перекрёстных связей, поэтому используя правила преобразования структурных схем, проведём преобразование [4], в результате которого структура модели бурильной колонны сведена к виду на рис. 2.

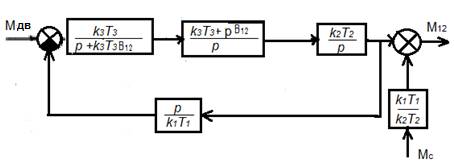
Рисунок 2 – Структурная модель с учётом преобразования

перекрёстных связей

Здесь M12 – момент, приложенный к буровому инструменту,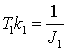, , 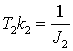T3k3 = C12, где T1, T2, T3 – постоянные времени интеграторов прямого канала передачи; k1, k2, k3 – статические коэффициенты передачи интегрирующих звеньев; J1 – момент инерции бурильной колонны, приведённый к валу привода, J2 – момент инерции утяжеленного низа бурильной колонны, приведённый к валу привода.

Разомкнутая модель структуры имеет вид, представленный на рис. 3.

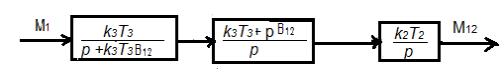
Рисунок 3 – Разомкнутая структура модели бурильной колонны

Передаточная функция разомкнутой структуры равна

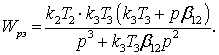                                   (8)

Иными словами, передаточная функция определяет  бурильную колонну как структурно неустойчивое астатическое звено третьего порядка.

Проведём исследование структурной модели в пакете Math Lab с учётом конкретных значений параметров бурения и привода ротора. Для моделирования были взяты данные с разведочной скважины №123 Западно-Тиманского месторождения.

Значения основных параметров колонны бурильных труб приведены в таблицах 1 и 2. Глубина бурения 2500м, т.е. lбк = 2500 м.

Таблица 1. Верхняя часть бурильной колонны.

Наружный диаметр, D

Внутренний

диаметр, d

Длинна

 трубы

Длинна участка

Масса ед. длины трубы

0,127 м

0,108 м

12 м

2400 м

33 кг/м

 

Таблица 2. Нижняя (утяжеленная) часть бурильной колонны.

Наружный диаметр, D

Внутренний

диаметр, d

Длинна

 трубы

Длинна участка

Масса ед. длины трубы

0,165 м

0,07 м

12 м

100 м

133 кг/м

 

Считаем, что при установившемся уравновешенном режиме бурения Mс  ≈ Mкр.

Рассчитаем коэффициент жесткости бурильной колонны:

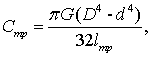                                               (9)

где G = 7,7 1010 Па – упругий модуль сдвига.

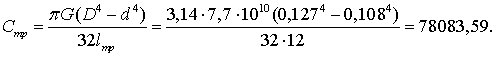
Будем считать, что крутильная податливость (величина, обратная жесткости) будет равна изгибной. Тогда эквивалентная податливость отдельной трубы будет равна сумме крутильной и изгибной податливости. Величина эквивалентной жесткости трубы при таком условии составляет:

                                                   (10)

Суммарный коэффициент жесткости:

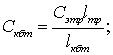                                                   (11)

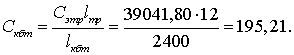
Для построения структурной модели колонны бурильных труб необходимо осуществить приведение момента инерции и коэффициента жесткости к валу привода - выходной вал редуктора. Будем считать связь абсолютно жесткой, i = 6,3.

Приведенная жесткость

                                              (12)

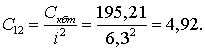
Исходя из экспериментальных данных с буровой, примем коэффициент вязкого трения β12=0,426.

Вычислим моменты инерции верхней и нижней частей бурильной колонны. Момент инерции бурильной трубы:

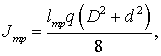                                                   (13)

где    lтр – длина бурильной трубы;

q – масса единицы длины трубы;

D, d – внешний и внутренний диаметр трубы.

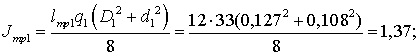
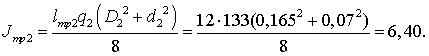
Суммарный момент инерции колонны труб определяется выражением:

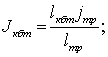                                              (14)

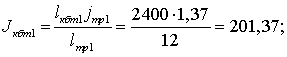
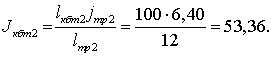
Тогда, приведенный момент инерции колонны бурильных труб к валу двигателя:

;                                                (15)

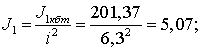
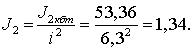
Результаты расчетов представлены в таблице 3.

Таблица 3. Результаты расчетов.

J1

J2

C12

Β12

5,07 кгм2

1,34 кгм2

4,92 Нм

0,426

 

Структурная схема исследования приведена на рис. 4.

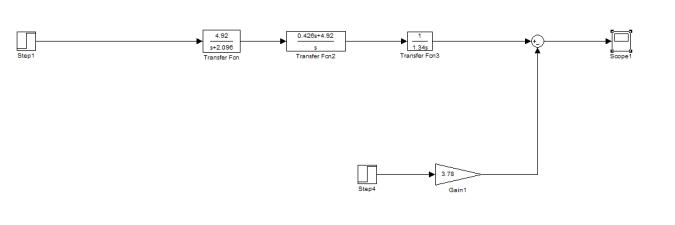
Рисунок 4 – Структурная схема исследования

Без введения корректирующего дифференцирующего звена связи при подаче возмущения значение момента на выходе структуры неограниченно растет, что подтверждает утверждение о структурной неустойчивости колонны бурильных труб, как объекта автоматического управления.

Результаты моделирования при Mс =11200 Нм и Mкр = 11300 Нм представлены на рис. 5. По вертикальной оси отложен крутящий момент в Нм, по горизонтальной оси время в секундах.

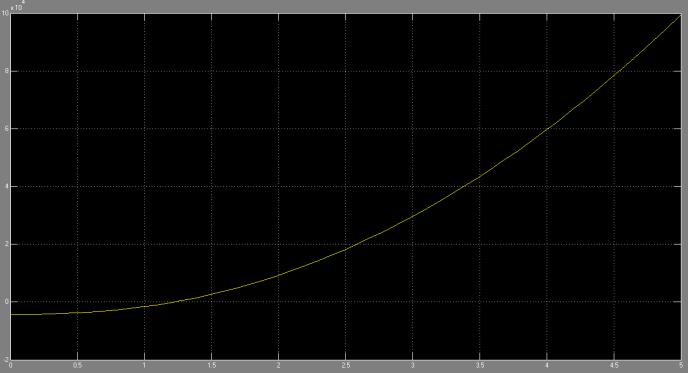
Рисунок 5 – Осциллограмма крутящего момента без

корректирующих звеньев

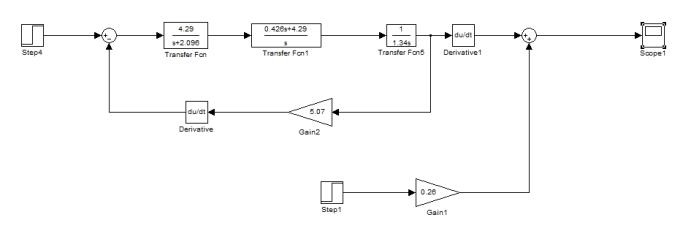
Рисунок 6 – Структурная схема исследования с корректирующим дифференциальным звеном

Как показало моделирование, для ограничения роста момента, к модели, предложенной в статье [4], необходимо добавить дифференцирующее звено, как показано на рис. 6. График зависимости момента М12 от времени представлен на рис. 7.

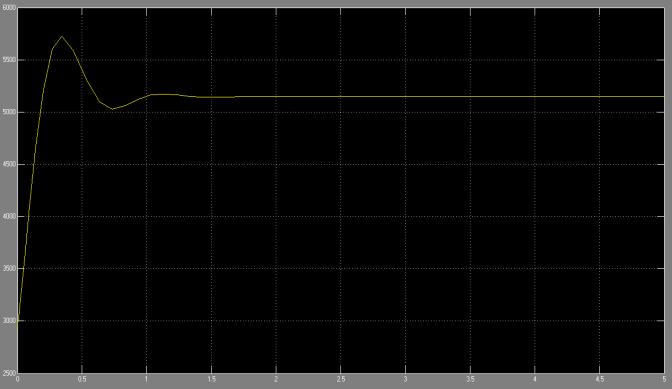
Рисунок 7 – Осциллограмма крутящего момента с

корректирующими звеньями

На рисунках 8 и 9 приведены кривые изменения крутящего момента (переходный процесс) для различных глубин бурения. Глубина бурения определяется соотношением моментов инерции J1 и J2. Утяжеление забойной части бурильной колонны приводит к снижению частоты крутильных автоколебаний, но при этом резко возрастает амплитуда автоколебаний, что приводит к снижению устойчивости процесса бурения и снижению скорости проходки скважины вследствие скручивания бурильной колонны.

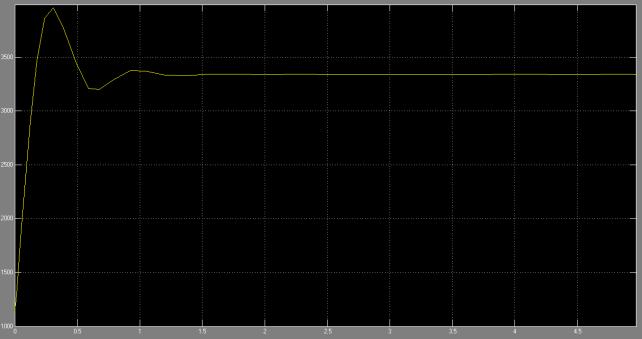
Рисунок 8 – Осциллограмма крутящего момента при J2/J1=0,1

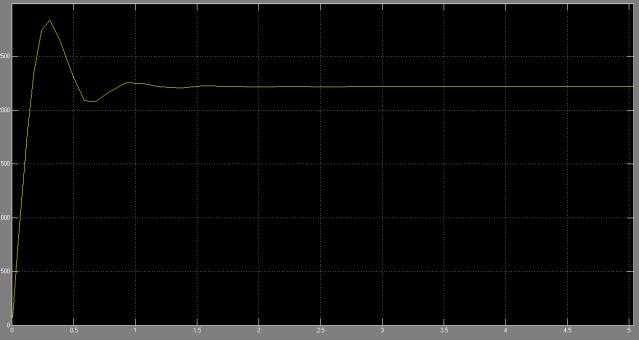
Рисунок 9 – Осциллограмма крутящего момепнта при J2/J1=0,01

Выводы:

1. Передаточная функция разомкнутой структуры модели бурильной колонны определяется интегратором третьего порядка, что характеризует колонну бурильных труб как структурно неустойчивый объект управления.

2. Являясь структурно неустойчивым звеном, бурильная колонна как объект автоматического регулирования, при управлении процессом углубления скважины требует введение коррекции её динамических характеристик.

3. Утяжеление забойной части бурильной колонны приводит к резкому возрастанию амплитуды автоколебаний, снижению устойчивости процесса бурения, и как следствие, к большему потреблению мощности привода, снижению его коэффициента полезного действия, и снижению скорости проходки скважины. вследствие скручивания бурильной колонны.

Литература:

1. Юнин Е. К., Хегай В. К. Динамика глубокого бурения. М.: Недра, 2004. – 286 с.

2. Юнин Е. К., Хегай В. К. Основы механики глубокого бурения. Курс лекций. – М.: ООО «Издательский дом Недра», 2010. – 163с.: ил.

3. Быков И. Ю., Заикин С. Ф., Перминов Б. А. Колонна бурильных труб в процессе углубления скважины, как объект автоматического регулирования // Строительство нефтяных и газовых скважин на суше и на море. – 2012. – №10. – С. 13 – 17.

4. Быков И. Ю., Заикин С. Ф., Перминов Б. А., Перминов В. Б., Полетаев С. В., Ягубов З. Х Исследование структурной модели бурильной колонны. Научно-методический электронный журнал "Концепт", 2014. Т. 20. – С. 2316 – 2320.