Шанкибаев Б.Н.

Республика Казахстан,

Центрально-Азиатский университет

Новый подход к решению задач

целочисленного программирования

Известно, что задача отыскания оптимального целочисленного решения задачи линейного программирования является довольно сложной.

В данной работе рассмотрен так называемый «метод сокращения невязок», представленный в работах [1 - 3].

Изложим указанный метод на примере решения «задачи о ранце».

Рассматривается следующая задача: найти минимальное значение функции

(1)

при ограничениях:

(2)

Здесь предполагается, что .

Алгоритм «метода сокращения невязок» для решения «задачи о ранце» в окончательном варианте опубликован в работе [4].

Введём следующие термины и обозначения.

Пусть некоторая линейная комбинация значений , . Обозначим через - коэффициент при переменной в комбинации . Назовём вектор допустимой комбинацией, если компоненты удовлетворяют условиям:

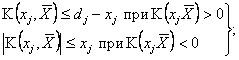₍₃₎

при и ; (4)

при ; (5)

при и ; (6)

при и . (7)

Здесь параметры , , определяются по ходу алгоритма и являются переменной величиной.

Алгоритм решения задачи о ранце.

Шаг 0. Полагаем: .

Каждому вектору , , присваивается метка (признак допустимости).

Шаг 1. Среди множества векторов , метка которых , выбирается вектор с наименьшим отношением .

Если множество таких векторов пусто, переходим на шаг 9. Принимается .

Шаг 2. Полагаем , , . Если , переходим на шаг 7. При переходим на шаг 4.

Шаг 3. При выполнении условий (3) по новой комбинации по каждому вектору , для которого , определяется новый вектор с параметрами (8)

и по каждому вектору , для которого , определяется новый вектор : (9)

Переходим на шаг 5.

Шаг 4. При выполнении условий (3) по каждому вектору , для которого , определяется новый вектор с параметрами (8), и по каждому вектору , для которого , определяется новый вектор с параметрами (9).

Шаг 5. Если , то выполняется шаг 6.

Присваивается метка вектору , если имеет место:

. (10)

Присваивается метка вектору , если имеет место:

. (11)

Переходим на шаг 1.

Шаг 6. Полагаем . Вектору присваивается или метка , если , (12)

или метка , если выполнено (11).

Шаг 7. Полагаем , если только значение изменилось. При переходим на шаг 9.

Шаг 8. Среди множества векторов с метками выбирается вектор с наименьшим отношением . Если множество таких векторов пусто, переходим на шаг 9, иначе на шаг 2.

Шаг 9. Полагаем: . Конец решения.

Алгоритм окончен.

Следующие четыре леммы позволяют сократить количество допустимых компонент, определяемых на шагах 3 и 4 алгоритма.

Лемма 1. Для любых неотрицательных чисел и , для которых выполнены условия

,

имеет место неравенство

.

Итак, на основании леммы 1, при проведении шага 2 по вектору , у которого , нет надобности находить новые компоненты вектора со значением по векторам , для которых

.

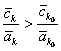Лемма 2. Для любых неотрицательных чисел и , для которых выполнены

имеет место неравенство

.

Итак, на основании леммы 2, при недопустимости вектора , у которого и наличии компоненты , у которой , при условии допустимости, необходимо строить новую компоненту с меткой .

Лемма 3. При неотрицательных элементах и при

,

имеет место неравенство

.

Следствие 1. При наименьшая комбинация вида

при достигается при наибольшем отношении .

Лемма 4. При неотрицательных элементах и при

,

имеет место неравенство

Следствие 2. При наименьшая комбинация вида

при достигается при наименьшем отношении .

Общая схема доказательства оптимальности и конечности алгоритма сокращения невязок.

Доказательство складывается из следующих предложений.

1. По ходу алгоритма строятся все простейшие допустимые комбинации, имеющие место после каждой итерации алгоритма.

Допустимую комбинацию называем простейшей, если она не может быть представлена как сумма хотя бы двух простейших допустимых комбинаций с одинаковыми знаками .

2. Каждая новая комбинация строится как простая линейная комбинация (плюс или минус) двух допустимых комбинаций, образованных после предыдущей итерации алгоритма.

3. Область допустимости, в виду неуклонного уменьшения и требований (4), (6), (9), сужается после очередного выполнения условия . Это гарантирует сходимость алгоритма.

Справедливость предположений «2» и «3» непосредственно вытекает из действий алгоритма (формулы (8), (9), (10)).

Убедимся в справедливости предположения «1».

Действительно, в исходной позиции все компоненты вектора составляют полный набор и являются простейшими. Допустим, что после первой итерации значение . Тогда дополнительными простейшими комбинациями окажутся комбинации, компоненты которых будут соответствовать значениям

Эти комбинации вместе с исходными комбинациями будут составлять полный набор. Если допустить, что на следующей итерации рабочей комбинацией выбрана комбинация, соответствующая компоненте , то дополнительными простейшими комбинациями будут комбинации, соответствующие компонентам:

,

которые окажутся допустимыми. В этих комбинациях берётся знак «+», если соответствующие им параметры разного знака и знак «-», если знаки их одинаковы. Из числа комбинаций выбрасываются идентичные, т.е. те, которые повторяются с кратными коэффициентами. Например, если и одного знака, то комбинация с компонентой

не берётся, так как она уже есть в наборе.

Таким образом, и после этой итерации допустимые комбинации составят полный набор.

Используя метод математической индукции, легко убедится в справедливости этого утверждения после каждой итерации алгоритма.

Кажущее увеличение числа комбинаций не будет большим, так как многие из них окажутся недопустимыми. С другой стороны, область допустимости ограничена сверху и эта граница всё время понижается, и количество комбинаций с выходами в область допустимых неуклонно уменьшается. Процесс заканчивается, когда множество допустимых комбинаций с меткой окажется пустым, или окажется, что .

Очевидны следующие два утверждения.

4. После выполнения каждой итерации алгоритма получается оптимальное решение условной задачи, которая отличается от исходной только заменой на .

5. Оптимальная комбинация, т.е. комбинация приводящая к оптимальному решению, находится среди простейших допустимых комбинаций.

Доказательство «4». Действительно, после первой итерации предложение справедливо. Используем метод математической индукции, т.е. пусть предложение справедливо после -той итерации. Так как после каждой итерации строится полный набор простейших допустимых комбинаций, то на основании выбора решающей комбинации очевидно, что и после -й итерации предложение справедливо.

Доказательство «5». Ясно, что можно предположить, что множество допустимых комбинаций с меткой не пусто. Так как в противном случае это означает, что мы уже прошли через оптимальное решение.

Если предположить, что «5» не выполняется, то:

а) есть допустимая комбинация, приводящая к значению целевой функции, меньшей чем оптимальное значение;

б) есть допустимая комбинация, приводящая к значению целевой функции, большей чем оптимальное значение.

Случай а) противоречит тому, что исследуемая комбинация оптимальная. Случай б) противоречит предположению «4».

Литература

1. Шанкибаев Б.Н. Условия оптимальности и алгоритмы решения целочисленных распределительных задач // Диссертация на соискание ученой степени кандидата физико-математических наук. М., ЦЭМИ АН СССР, 1972.

2. Шанкибаев Б.Н. Целочисленная распределительная задача //Труды 6-й школы по математическому программированию, М., 1975, с. 259-289.

3. Шанкибаев Б.Н. Об одном методе решения задачи о ранце //Материалы 3-й Всесоюзной школы «Дискретная оптимизация и компьютеры», М., 1987, с. 146-147.

4. Шанкибаев Б.Н. Математическое программирование. Монография. Алматы, «Эверо», 2004, 268 с.