Карачун В.В., Мельник В.М.
Національний технічний університет
України «КПІ»
ЧИСЕЛЬНИЙ АНАЛІЗ ПЕРЕХІДНОГО ПРОЦЕСУ В СТРУНІ
Розв’язок хвильового рівняння
![]() наводиться в багатьох джерелах
з теорії коливань і рівнянь математичної фізики. Разом з тим, чисельний метод,
що реалізується на комп'ютері, відкриває можливість за допомогою однієї програми вирішувати широке коло задач при різних комбінаціях початкових
та граничних умов, а також для різноманітних форм збурюючих чинників.
наводиться в багатьох джерелах
з теорії коливань і рівнянь математичної фізики. Разом з тим, чисельний метод,
що реалізується на комп'ютері, відкриває можливість за допомогою однієї програми вирішувати широке коло задач при різних комбінаціях початкових
та граничних умов, а також для різноманітних форм збурюючих чинників.
Розглянемо підготовку задачі
до розв’язання її на ЕОМ.
Перейдемо від неперервних
змінних до дискретних -
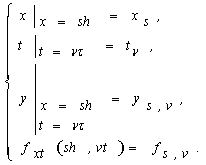 (1)
(1)
Замінимо частинні
похідні відповідними співвідношеннями, наприклад, таким чином:
 (2)
(2)
Якщо рівняння (2)
роз’язати відносно ![]() , то отримаємо
розрахункове співвідношення для так званої явної схеми інтегрування
, то отримаємо
розрахункове співвідношення для так званої явної схеми інтегрування
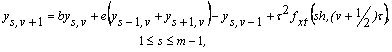 (3)
(3)
де ![]() ;
; ![]() ;
; ![]() .
.
Перш ніж
програмувати формулу (3), визначимося з формою представлення стану струни в довільний поточний момент
часу ![]() . Функцію
. Функцію ![]() будемо представляти у вигляді масиву Yt такої структури
будемо представляти у вигляді масиву Yt такої структури
|
|
-1 |
0 |
1 |
2 |
... |
m |
||||||||
|
Yt |
m |
|
|
|
... |
|
|
|
|||||||
де m - число
розрахункових відрізків, на які
поділяється струна, ![]() (
(![]() - довжина струни,
- довжина струни, ![]() - крок вздовж
координати
- крок вздовж
координати ![]() , як вже відзначалося
раніше, вираз (3)).
, як вже відзначалося
раніше, вираз (3)).
Початковий стан струни (за ![]() ) визначимо відповідною підпрограмою-функцією Yn. Але, крім цього ще необхідно задати швидкості точок струни (підпрограма
Dyn). Скористаємося щойно згаданими
функціями для обчислення значень
) визначимо відповідною підпрограмою-функцією Yn. Але, крім цього ще необхідно задати швидкості точок струни (підпрограма
Dyn). Скористаємося щойно згаданими
функціями для обчислення значень ![]() за умови
за умови ![]() . Для цього запишемо ряд Тейлора -
. Для цього запишемо ряд Тейлора -
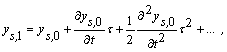 (4)
(4)
обмежившись в ньому
трьома першими доданками. Тут ![]() означає
означає 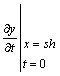 , а
, а ![]() відповідає
відповідає 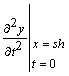 .
.
Значення другої
похідної у формулі (4) визначаємо за умови ![]() :
:
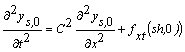 . (5)
. (5)
Підставляємо (5) в (4)
-
![]() . (6)
. (6)
Формула (6)
покладена в основу підпрограми Init,
яка формує масиви ![]() (для
(для ![]() ) і Yt (для
) і Yt (для ![]() ), а також задає
), а також задає
![]() .
.
procedure Init;
var g,s:integer;
begin
for s:=0 to m do Yp[s]:=Yn(s*Hx);
for s:=1 to m-1 do
Yt[s]:=Yp[s]+Dyn(s*Hx)*Tau+E/2*(Yp[s-1]-2*Yp[s]+Yp[s+1])+
Tau2/2*Fxt(s,0);
g:=round(Xg(0)/Hx);
if Mg>0 then Yt[g]:=Yp[g]+Dyg*Tau+
sqr(Tau)/2*(Mh*fxt(g,0)+Fg(0)+
Ts/Hx*(Yp[g-1]-2*Yp[g]+Yp[g+1]))/(Mg+Mh);
case Ngl of
1:Yt[0]:=Yl(Tau);
2:if g>0 then Yt[0]:=Yp[0]+Dym0*Tau+
sqr(Tau)/2*(Ts*(Yp[1]-Yp[0])/Hx+
fxt(0,0)*Mh/2+Fl(0))/(M0+Mh/2)
else Yt[0]:=Yp[0]+(Dyn(0)*Mh/2+
Dym0*M0+Dyg*Mg)/(M0+Mh/2+Mg)+
(Ts*(Yp[1]-Yp[0])/Hx+fxt(0,0)*Mh/2+
Fl(0)+Fg(0))*sqr(Tau)/2/(M0+Mh/2+Mg);
3: if g>0 then Yt[0]:=Yp[0]+Tau*(Dyn(0)+Mh/2+
Dym0*M0)/(M0+Mh/2)+
sqr(Tau)/2/(M0+Mh/2)*(Ts*(Yp[1]-Yp[0])/Hx+
C0*(Ylk(0)-Yp[0]))
else Yt[0]:=Yp[0]+Tau*(Dyn(0)*Mh/2+
Dym0+M0+Dyg*Mg)/(M0+Mg/2+Mg)+
sqr(Tau)/2/(M0+Mh/2+Mg)*(Ts*Yp[1]-
Yp[0]+C0*(Ylk(0)-Yp[0])+fxt(0,0)*Mh/2+Fg(0))
end;
case Ngr of
1: Yt[m]:=Yr(Tau);
2: if g<m then Yt[m]:=Yp[m]+Tau*(Mh/2*Dyn(m*Hx)+
Mm*DyMm)/(Mh/2+Mm)+
sqr(Tau)/2/(Mh/2+Mm)*(Ts*(Yp[m-1]-
Yp[m])/Hx+Fr(0)+Fxt(m*Hx,0)*Mh/2)
else Yt[m]:=Yp[m]+Tau*(Mh/2*Dyn(M*Hx)+
Mm*DyMm+Mg*Dyg)/(Mh/2+Mm+Mg)+
sqr(Tau)/2/(Mm+Mh/2+Mg)*(Ts*(Yp[m-1]-
Yp[m])/Hx+Fr(0)+Fg(0)+Fxt(m*Hx,0)*Mh/2);
3:if g<m then Yt[m]:=Yp[m]+Tau*(Mm*DYMm+
Mh/2*Dyn(M*Hx))/(Mm+Mh/2)+
sqr(Tau)/2/(Mm+Mh/2)*(Ts*(Yp[m-1]-
Yp[m])/Hx+C1*(Yrk(0)-Yp[m])+
fxt(m*Hx,0)*Mh/2+Fr(0))
else Yt[m]:=Yp[m]+Tau*(Mm*DyMm+Mh/2*Dyn(M*Hx)+
Mg*Dyg)/(Mm+Mg+Mh/2)+
sqr(Tau)/2/(Mm+Mg+Mh/2)*(Ts*(Yp[m-1]-
Yp[m])/Hx+C1*(Yrk(0)-Yp[m])+
fxt(m*Hx,0)*Mh/2+Fr(0)+Fg(0))
end;
T:=Tau
end;
Тут Type CoefR=array[-1..200]of real;
Коефіцієнти Tau, Tau2, Е, що використовуються в
процедурі Init, як і ряд інших
коефіцієнтів, що будуть залучені далі, обчислюються
процедурою CoefB (буде наведена
нижче).
Звернемося тепер до
формули (3), що реалізує явну схему. Вона «обслуговує» внутрішні вузли сітки,
яка покриває область ![]() , в яких відсутня маса
, в яких відсутня маса ![]() . Якщо ж маса
. Якщо ж маса ![]() в момент часу,
що розглядається, знаходиться у вузлі з номером
в момент часу,
що розглядається, знаходиться у вузлі з номером ![]() тоді для цього
вузла повинна виконуватися умова
тоді для цього
вузла повинна виконуватися умова
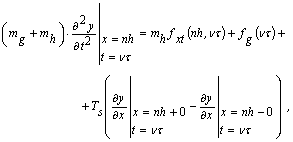 (7)
(7)
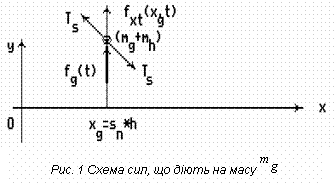
де ![]() - маса відрізку
струни довжини
- маса відрізку
струни довжини ![]() .
.
Перейдемо в умові (7)
до дискретних змінних
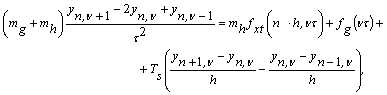
звідки

або після зведення подібних -
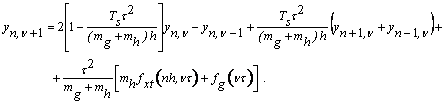
Після введення коефіцієнтів ![]()
![]() (8)
(8)
де 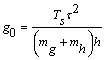 ,
, ![]() ,
, 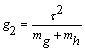 .
.
Зовнішні вузли сітки
з номерами ![]() і
і ![]() «обслуговуються»
граничними умовами. Розглянемо граничні
умови послідовно:
«обслуговуються»
граничними умовами. Розглянемо граничні
умови послідовно:
![]() . (9)
. (9)
![]() ,
,
звідки 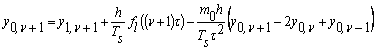
або

Ввівши
коефіцієнти ![]() , приводимо
, приводимо ![]() до вигляду
до вигляду
![]() , (10)
, (10)
де ![]() ;
; ![]() ;
; ![]() .
.
Співвідношення
(10) слушне за умови, коли ковзаюча вздовж
струни маса в даний момент часу не виявляється на лівому кінці струни. В іншому
випадку ця маса приєднується до ![]() , а сила, діюча на неї, додається до
, а сила, діюча на неї, додається до ![]() і тоді:
і тоді:
![]() , (11)
, (11)
де 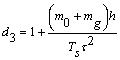 ;
; ![]() ,
, ![]() .
.
Гранична
умова у випадку, коли маса ![]() відсутня, або знаходиться не на лівому кінці струни, дає при переході в дискретну форму наступне -
відсутня, або знаходиться не на лівому кінці струни, дає при переході в дискретну форму наступне -
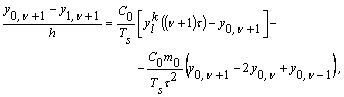
звідки
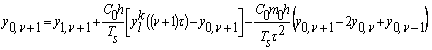 .
.
Після зведення подібних, маємо:
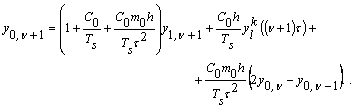
Введемо
коефіцієнти ![]() . Тоді отримаємо -
. Тоді отримаємо -
![]() , (12)
, (12)
де ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Якщо ж маса знаходиться на лівому кінці струни, тоді замість співвідношення (12)
маємо:
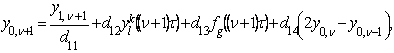 (13)
(13)
де 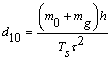 ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Переходячи до
правого кінця, будемо мати:
![]() (14)
(14)
Гранична умова якщо
що маса ![]() не знаходиться на правому кінці струни, в
дискретній формі дає -
не знаходиться на правому кінці струни, в
дискретній формі дає -
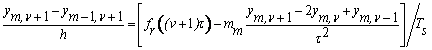 ,
,
звідки
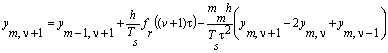 .
.
Зводимо подібні
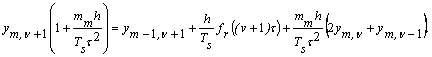
Введемо коефіцієнти ![]()
![]() :
:
![]() (15)
(15)
де ![]() ;
; ![]() ;
; ![]() .
.
Якщо ж в момент часу,
що розглядається, маса ![]() знаходиться на правому кінці струни, тоді -
знаходиться на правому кінці струни, тоді -
![]() (16)
(16)
де 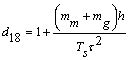 ;
; ![]() ;
; ![]() .
.
І нарешті, гранична
умова за відсутності маси ![]() на правому кінці
на правому кінці

дає
можливість відзначити:
![]() Зводимо
подібні
Зводимо
подібні
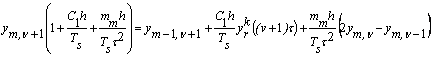
Застосуємо
коефіцієнти ![]() :
:
![]() , (17)
, (17)
де ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Якщо маса ![]() знаходиться на правому кінці струни, тоді -
знаходиться на правому кінці струни, тоді -
![]() (18)
(18)
де 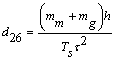 ;
; ![]() ;
; ![]() ;
;
![]() ;
;![]() .
.
Співвідношення (3),
(8)…(17) покладені в основу підпрограми Stept, що реалізує крок за часом за
явною схемою.
Procedure Stept;
Var
s, N:integer;
Y:CoefR;
Begin
for s:=1 to m-1 do
у[s]:=b*Yt[s]+е*(Yt[s-1]+Yt[s+1])-Yp[s]+Tau2*fxt(s*Hx, Т+Tau/2);
N:=round
(Xg(Т)/Hx);
if (N>0)and(N<m) then
Y[N]:=G1*Yt[N]-Yp[N]+G0*(Yt[n-1]+
Yt[n+1])+G2*(Fxt(N*Hx, Т)+Fg(Т));
Т:=Т+Tau;
сase Ngl of
1:
Y[0]:=Yl(Т);
2: if N>0
thenY[0]:=Y[1]/D0+D1*Fl(Т)+D2*(2*Yt[0]-Yp[0])
else
Y[0]:=Y[1]/D3+D4*(Fl(Т)+Fg(Т))+D5*(2*Yt[0]-Yp[0]);
3: if N>0
then Y[0]:=Y[1]/D7+D8*Ylk(Т)+D9
*(2*Yt[0]-Yp[0])
else Y[0]:=Y[1]/D11+D12*Ylk(Т)+
D13*Fg(Т)+D14*(2*Yt[0]-Yp[0]);
end;
case Ngr of
1: Y[m]:=Yr(Т);
2: if
N<m then
Y[m]:=Y[m-1]/D15+D16*Fr(Т)+D17*(2* Yt[m]-Yp[m])
else
Y[m]:=Y[m-1]/D18+D19* (Fr(Т)+
Fg(Т))+D20*(2*Yt[m]-Yp[m]);
3: if
N<m then Y[m]:=Y[m-1]/D23+D24*Yrk(Т)+D25*(2*Yt[m]-Yp[m])
else Y[m]:=Y[m-1]/D27+D28*Yrk(Т)+D29*Fg(Т)+D30*(2*Yt[m]-Yp[m]);
end;
Y[-
1]:=m; Yp:=Yt; Yt:=Y
end;