Айпанов Ш.А.

Казахский национальный университет им. аль-Фараби, Алматы, Казахстан

ОПТИМАЛЬНЫЙ СПУСК КОСМИЧЕСКОГО АППАРАТА

В АТМОСФЕРЕ

Рассматривается задача мягкой посадки космического аппарата (КА) в заданную точку на поверхности планеты за кратчайшее время. Предполагается, что двигатель развивает постоянную тягу, а управление движением КА осуществляется путем изменения направления вектора тяги. Необходимо отметить, что торможение КА производится не только с помощью двигательной установки, для минимизации расхода топлива надо также эффективно использовать воздействие аэродинамической силы сопротивления. Схема спуска показана на рис. 1.

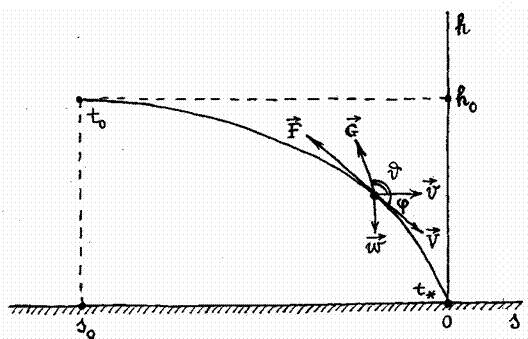
Рис. 1. Схема спуска КА в атмосфере планеты

Уравнения движения КА (с учетом изменения силы притяжения и плотности атмосферы в зависимости от высоты над поверхностью планеты) имеют вид [1]

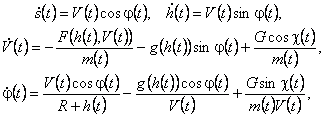(1)

где – координата КА относительно точки посадки, – высота над поверхностью планеты, – скорость КА, – угол наклона траектории к горизонту (), – управляемая переменная, равная углу между – вектором скорости КА и – вектором тяги, – радиус планеты, – тяга двигателя (). Процесс рассматривается в интервале , где за начальный момент времени принят , а конечный момент заранее не известен, надо найти наименьшее возможное его значение.

Масса КА уменьшается по мере расхода топлива по следующему закону где – начальная масса КА, – расход топлива в единицу времени (). Ускорение силы тяжести зависит от высоты над поверхностью планеты и вычисляется по формуле где – гравитационная постоянная планеты. Аэродинамическая сила сопротивления равна где – коэффициент аэродинамического сопротивления, – характерная площадь, – плотность атмосферы. Предполагается, что плотность атмосферы в зависимости от высоты над поверхностью планеты уменьшается по экспоненциальному закону , где – плотность атмосферы непосредственно над поверхностью планеты, – показатель, характеризующий относительную скорость изменения плотности атмосферы.

Поскольку в конечный момент времени для переменной – угла наклона траектории к горизонту, как правило, какие-либо условия не ставятся, произведем замену переменных. Введем следующие обозначения: – вертикальная компонента скорости КА, – горизонтальная компонента скорости КА, – новая управляемая переменная, равная углу между – горизонтальной составляющей скорости КА и – вектором тяги. С использованием соотношений

систему дифференциальных уравнений (1) можно переписать в виде

(2)

где

Решим задачу при следующих значениях параметров:

Здесь значения и взяты из модели атмосферы Марса, приведенной в [2]. Пусть начальные условия имеют вид

(3)

Конечные условия выберем в виде

(4)

Отметим, что начальное условие не задано, т.е. левый конец траектории системы является подвижным, тогда как правый конец закреплен.

Таким образом, требуется решить задачу оптимального быстродействия (ЗОБ)

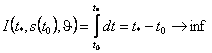(5)

при дифференциальных связях (2) и краевых условиях (3), (4).

В расчетах, приведенных в [1], отсутствуют конечные условия (4) и решается задача приближенного синтеза оптимального управления для системы со свободными правыми концами траекторий, т. е. хотя и минимизируется скорость КА в момент отключения двигателя, но все же не гарантируется точное равенство ее нулю. В отличие от этой работы здесь ставится задача совершения мягкой посадки ( при ) в заданной точке на поверхности планеты (). Для решения этой задачи можно применить метод квазилинеаризации [3].

Обозначим через оптимальную траекторию, через оптимальное управление в исходной нелинейной ЗОБ (2)-(5). Используя принцип максимума Понтрягина, паре поставим в соответствие сопряженный вектор . Из необходимых условий оптимальности можно вывести формулы для определения искомого оптимального управления:

Отметим здесь некоторые особенности применения метода квазилинеаризации, обусловленные подвижностью левого конца траектории системы. Обозначим через решение двухточечной краевой задачи (ДТКЗ), получаемой на -ом шаге квазилинеаризации, где векторы

, .

На -ой итерации получается ДТКЗ для системы из восьми линейных дифференциальных уравнений следующего вида:

(6)

где – некоторые матрицы, – некоторые векторы, получаемые в процессе квазилинеаризации; начальное множество

;

конечная точка . ДТКЗ (6) соответствует некоторой линейно-квадратичной ЗОУ с подвижным левым концом и закрепленным правым концом траектории системы. Поэтому при применении принципа максимума возникает дополнительное условие трансверсальности [5], которое в данном случае имеет вид .

Используя далее метод, предложенный автором в [4], ДТКЗ (6) можно свести к задаче Коши, в которой начальные условия будут иметь вид

Если рассматривать второе соотношение как систему линейных алгебраических уравнений относительно неизвестных , то начальные условия полностью определяются.

Варьируя величину , вычисляя методом квазилинеаризации соответствующий вектор и используя его как начальное значение сопряженного вектора в ДТКЗ принципа максимума, можно найти такое значение , при котором достигается выполнение конечных условий (4) с наименьшей относительной погрешностью.

Для реализации вышеизложенного алгоритма был разработан комплекс программ на алгоритмическом языке FORTRAN. Решение ЗОБ (2)-(5), полученное с использованием этих программ, представлено в табл. 1. Условия трансверсальности на левом и правом концах траектории также соблюдены:

Таким образом, определены – оптимальная траектория спуска КА и – оптимальная программа управления направлением вектора тяги.

Табл. 1. Оптимальные траектории и управление

в задаче спуска КА в атмосфере планеты Марс

t
с	км	км	км / с	км / с			градусы
0.00000	-40.79787	45.00000	-4.24264	4.24264	-0.95513	-0.29618	252.71756
0.73338	-37.70033	41.87013	-4.29179	4.20293	-0.93840	-0.34554	249.72932
1.46676	-34.63619	38.70686	-4.33317	4.15087	-0.90992	-0.41478	245.43624
2.20014	-31.61618	35.51738	-4.36234	4.08160	-0.85651	-0.51613	238.86551
2.93352	-28.65534	32.31307	-4.37203	3.98818	-0.74445	-0.66768	228.04497
3.66690	-25.77460	29.11252	-4.34919	3.86162	-0.49181	-0.87070	209.38337
4.40028	-23.00082	25.94726	-4.27151	3.69674	-0.01848	-0.99983	180.96803
5.13366	-20.35906	22.86538	-4.12087	3.50461	0.45254	-0.89174	153.17063
5.86704	-17.86368	19.91881	-3.90542	3.29844	0.70281	-0.71138	135.41569
6.60042	-15.52450	17.14887	-3.64152	3.07813	0.81216	-0.58343	125.75581
7.33380	-13.35277	14.58635	-3.34169	2.84173	0.86082	-0.50891	120.65248
8.06718	-11.35978	12.25329	-3.01785	2.59146	0.88202	-0.47120	118.17229
8.80056	-9.55365	10.16257	-2.68306	2.33339	0.88879	-0.45832	117.33800
9.53394	-7.93720	8.31731	-2.35059	2.07554	0.88663	-0.46249	117.60740
10.26732	-6.50734	6.71139	-2.03202	1.82573	0.87818	-0.47833	118.63641
11.00070	-5.25582	5.33135	-1.73572	1.59002	0.86499	-0.50178	120.17902
11.73408	-4.17083	4.15888	-1.46641	1.37197	0.84819	-0.52969	122.04665
12.46746	-3.23886	3.17352	-1.22547	1.17274	0.82875	-0.55962	124.09241
13.20084	-2.44626	2.35473	-1.01182	0.99163	0.80757	-0.58977	126.20478
13.93422	-1.78042	1.68338	-0.82284	0.82667	0.78544	-0.61894	128.30361
14.66760	-1.23044	1.14263	-0.65508	0.67516	0.76300	-0.64639	130.33631
15.40098	-0.78759	0.71828	-0.50477	0.53401	0.74073	-0.67181	132.27374
16.13436	-0.44547	0.39893	-0.36805	0.39985	0.71887	-0.69515	134.10676
16.86774	-0.20027	0.17605	-0.24106	0.26906	0.69747	-0.71661	135.84414
17.60112	-0.05101	0.04394	-0.11983	0.13748	0.67632	-0.73661	137.51321
18.33450	-0.00005	-0.00006	0.00000	0.00000	0.65481	-0.75579	139.16534
конечные условия	0.00000	0.00000	0.00000	0.00000	–	–	–

ЛИТЕРАТУРА

1. Кротов В.Ф., Гурман В.И. Методы и задачи оптимального управления. – М.: Наука, 1973.

2. Мороз В. И., Кержарович В. В., Краснопольский В. А. Инженерная модель атмосферы Марса для проекта «Марс-94» (Ма-90) // Космические исследования, 1991, т. 29, вып.1, с. 3-84.

3. Беллман Р., Калаба Р. Квазилинеаризация и нелинейные краевые задачи. – М.: Мир, 1968.

4. Айсагалиев С.А., Айпанов Ш.А., Злобина Е.Б. Прикладные задачи оптимального управления. – Алматы: Қазақ университетi, 2005.

5. Васильев Ф.П. Численные методы решения экстремальных задач. – М.: Наука, 1988.