УДК 519.6

Аманбаев Т.Р.

Южно-Казахстанский государственный университет им. М. Ауезова

РЕШЕНИЕ ЗАДАЧИ ОБ ОДНОМ КОНИЧЕСКОМ ТЕЧЕНИИ ВЯЗКОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ

Движение вязкой несжимаемой жидкости описывается с помощью системы, состоящей из уравнения Навье-Стокса и уравнения неразрывности [1]

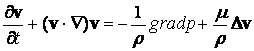, (1)

Здесь ρ, p, v, μ – плотность, давление, вектор скорости и коэффициент динамической вязкости среды. Рассмотрим стационарное течение внутри кругового конуса, возникающее за счет истечения жидкости (с расходом Q) из его вершины (диффузорное течение, Q>0 ). Все нижеприведенные рассуждения справедливы и для случая, когда в вершине конуса происходит сток жидкости (конфузорное течение, Q<0). Выбираем сферическую систему координат с полярной осью вдоль линии симметрии конуса в направлении скорости потока. Вершину конуса выбираем в качестве начала координат. Рассмотрим случай, когда движение жидкости будет чисто радиальным и осесимметричным, т.е. (θ – полярный угол сферической системы). Тогда уравнения (1) в выбранной системе координат запишутся в виде ()

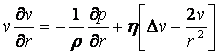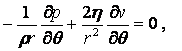
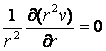, (2) (3)

Будем рассматривать движение жидкости в достаточном удалении от источника, когда скорость среды мала. Тогда нелинейным членом в левой части уравнения (2) можно пренебречь. Таким образом, далее рассматривается так называемое ползущее («медленное») течение внутри конуса (течение вдали от вершины конуса). Из последнего уравнения видно, что есть функция только θ. Введя функцию (где k=const) получаем из (3)

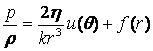(4)

Переписывая лапласиан от v через функцию u и принимая для удобства k равным η из (2) с учетом (4) получим уравнение: .

Отсюда видно, что как левая, так и правая части, зависящие соответственно только от θ и только от r, являются, каждая в отдельности, постоянной величиной, которую обозначим как -С . Итак, имеем систему

(5)

Рассмотрим более подробно первое уравнение с краевыми условиями: , ( - угол раствора конуса (в радианах)). С помощью замены это уравнение можно привести к однородному виду

, (6)

Краевые условия примут вид . Уравнение (6) имеет тривиальное решение, тождественно равное нулю. Но оно не удовлетворяет граничному условию на правом конце интервала, поэтому из рассмотрения исключается. Уравнение (6) заменой (при условии ) приводится к уравнению Лежандра

(7)

где n=2. С учетом краевых условий его решение после перехода к переменной можно записать в виде [2]

,

Окончательно для функции u имеем (постоянная С определяется из условия, что через любое сечение r=const проходит (в 1 сек.) одинаковый объем жидкости Q)

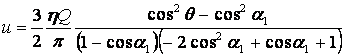(8)

При этом решение для v запишется в виде

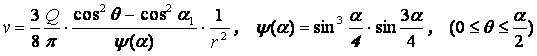
В частности, при углах раствора конуса, равных π/2 и π из (8) следует

α=π/2 : 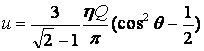; α=π:

Последний случай соответствует течению, возникающему в полупространстве от точечного источника (стока), находящегося на ограничивающей это полупространство плоскости. Анализ решения (8) показал, что при углах раствора конуса бóльших π (так называемые «обратные» конусы) появляются участки, где скорость меняет знак (но так, что Q=const>0). Это обстоятельство позволяет утверждать, что вдали от вершины ползущее («медленное») симметричное чисто диффузорное (везде расходящееся) или чисто конфузорное (везде сходящееся) течение жидкости возможно только для углов раствора конуса, не бóльших π. Некоторые примеры течения при α≤π проиллюстрированы на рисунке в виде распределения приведенной скорости в меридиональной плоскости конуса.

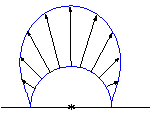
α=π/3 α=π/2 α=π

Литература

1. Ландау Л.Д., Лифшиц Е.М. Гидродинамика. М.: Наука, 1988.

2. Зайцев В.Ф., Полянин А.Д. Справочник по обыкновенным дифференциальным уравнениям. М.: Физматлит, 2001.