Математика / 5. Математическое моделирование

Сабо И.И.

Запорожский национальный университет, Украина

ИСПОЛЬЗОВАНИЕ МЕТОДА НАЧАЛЬНЫХ ФУНКЦИЙ ПРИ РЕШЕНИИ ЗАДАЧИ ОБ ИЗГИБЕ ТОЛСТОЙ ПЛИТЫ

В данной работе строится решение двумерной задачи теории упругости об изгибе толстой плиты в условиях плоской деформации при помощи символического метода начальных функций и решения гармонического уравнения для прямоугольника. Замена символических функций, удовлетворяющих гармоническому уравнению, соответствующими решениями гармонических функций позволяет получить решение данной задачи.

Символическое решение для полосы может быть получено из символического решения Власова В.З. для начальных функций, которое представляет собой суммы произведений дифференциальных операторов и соответствующих начальных функций [1, с. 355].

Дифференциальные операторы могут быть представлены либо в виде бесконечных операционных рядов, либо в виде символических формул (для плоско-деформируемого состояния) [1, с. 392].

В данной работе производится замена в символическом решении для полосы дифференциальных операторов решениями гармонического уравнения. Это позволяет получить решение задачи в рядах.

Найдем символическое решение для полосы, удовлетворяющее следующим граничным условиям:

, (1)

, (2)

, (3)

. (4)

Для вывода символического решения подставим символическое решение Власова В.З. в граничные условия (1) – (4). Далее формально будем работать с дифференциальными операторами как с тригонометрическими функциями. Решив полученную систему из четырех уравнений относительно четырех начальных функций, получим выражение начальных функций через функцию перемещения на границе .

Подставив полученные выражения в символическое решение для начальных функций, получим символическое решение для полосы удовлетворяющее граничным условиям (1) – (4):

, (5)

, (6)

, (7)

, (8)

. (9)

_{Полученные соотношения удовлетворяют уравнениям равновесия, уравнениям, выражающим связь между напряжениями и перемещениями, а также бигармоническому уравнению.}

Полученное символическое решение для полосы (5) – (9) содержит гармонические функции [2, с. 192]. Это позволяет нам подставлять точные решения гармонического уравнения для определенных областей, в зависимости от условия задачи.

_{Теперь рассмотрим практическое применение полученного символического решения на примере задачи об изгибе плиты.}

Рассмотрим задачу об изгибе плиты в условиях плоской деформации имеющей граничные условия (1) – (4) [1, с. 395].

Для решения данной задачи следует в символическое решение для полосы (5) – (9) подставить точное решение гармонического уравнения для прямоугольника.

Известно, что если гармоническая функция задана на области: , , а также заданы граничные условия: , , , , то её решением будет следующее выражение [3, с. 417]:

.

Коэффициенты , , , определяются формулами:

,

,

,

,

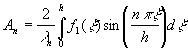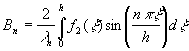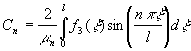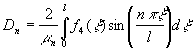где , .

Рассмотрим гармоническую функцию :

,

,

,

,

.

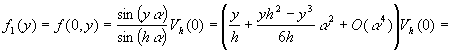
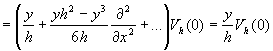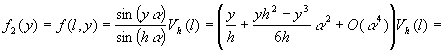
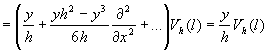Ее решением будет следующее выражение:

,

где

,

,

,

.

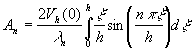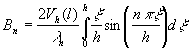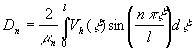Находим точное решение для функции , как сопряженной к функции . Выразив остальные гармонические функции как произведения содержащие либо и применив дифференциальные операторы к рядам, находим точное решение для напряжений и перемещений. Полученное таким образом решение совпадает с решением Власова В.З. [1, с. 407].

Применение метода начальных функций и замена гармонических функций соответствующими решениями позволяет получать выражения для напряжений и перемещений. Эффективность алгоритма показана на примере решения задачи об изгибе толстой плиты. Заменив гармонические функции, представленные в символическом виде, соответствующими решениями гармонического уравнения для прямоугольника, мы получили решение задачи в тригонометрических рядах.

Литература:

1. Власов В.З. Балки, плиты и оболочки на упругом основании / В.З. Власов, Н.Н. Леонтьев. – М.: Физматгиз, 1960. – 491 с.

2. Зельдович Я.Б. Элементы прикладной математики / Я.Б. Зельдович, А.Д. Мышкис. – М.: Наука, 1967. – 648 с.

3. Полянин А.Д. Справочник по линейным уравнениям математической физики / А.Д. Полянин. – М.: Физматлит, 2001. – 576 с.