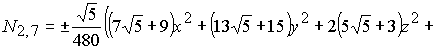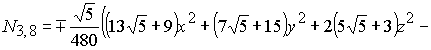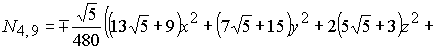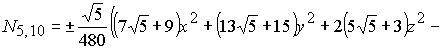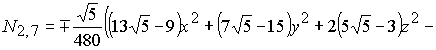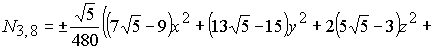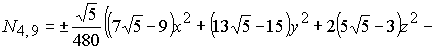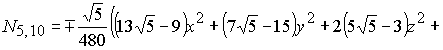Математика / 4. Прикладная математика

Зычкова Е.Э., Мотайло А.П., Тулученко Г.Я., Хомченко А.Н.

Херсонский национальный технический университет, Украина

Базисы икосаэдра на основе комбинаций
поверхностей вращения и плоскостей

Постановка проблемы. Алгебраический подход к построению интерполяционных базисов для фиксированной группы узлов и выбранного типа базисных функций приводит к единственному решению задачи или констатации факта отсутствия решения, т.е. невозможности построения базиса, удовлетворяющего указанным требованиям [1].

Геометрический поход в этом же случае часто позволяет находить множество (конечное или бесконечное) решений, что открывает возможности для решения задачи в оптимизационной постановке: определить базис с наилучшими аппроксимационными свойствами [2].

Анализ предшествующих публикаций. В рамках геометрического подхода авторами изучаются возможности построения интерполяционных базисов для системы узлов в вершинах икосаэдра на основе поверхностей вращения. В работе [3] построен и исследован базис икосаэдра на основе гармонической поверхности вращения третьего порядка, а в работе [4] – на основе комбинации уравнений однополостного гиперболоида и плоскости.

Цель публикации. Рассмотреть новые (по сравнению с работами [3-4]) сочетания вершин икосаэдра, которые являются инцидентными поверхностям вращения и плоскостям. Построить базисные функции для этих случаев и исследовать аппроксимационные свойства новых базисов.

Основная часть. Для сохранения единого подхода к изложению материала продолжим рассмотрение построения базиса икосаэдра на примере базисной функции для узла (рис. 1).

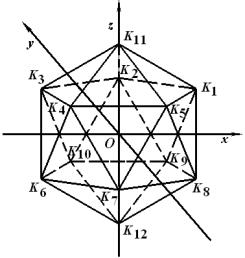
. Рис. 1. Икосаэдр

В работе [3] поверхность нулевого уровня базисной функции является гармонической поверхностью вращения третьего порядка и проходит через все вершины икосаэдра, кроме . В работе [4] поверхность нулевого уровня базисной функции состоит из однополостного гиперболоида,

который проходит через две группы вершин и , и плоскости, перпендикулярной оси вращения гиперболоида и проходящей через вершину .

Рассмотрим два других случая сочетания вершин:

1) поверхность нулевого уровня базисной функции проходит через вершины и , а плоскость через вершины ;

2) поверхность нулевого уровня базисной функции проходит через вершины и , а плоскость через вершины .

Таким образом, уравнение базисной функции в системе координат как на рис. 1 будет иметь вид:

,

(1)

где 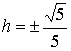; коэффициенты находятся из системы (2) или (3):

;

(2)

,

(3)

каждая из которых описывает условия (соответствующие рассмотренным выше случаям 1) и 2)) удовлетворения функцией (1) интерполяционной гипотезе Лагранжа.

Первый множитель в формуле (1) является уравнением поверхности вращения. Второй множитель является уравнением плоскости. Он обращается в ноль для группы узлов (в этом случае ) и для группы узлов (в этом случае ).

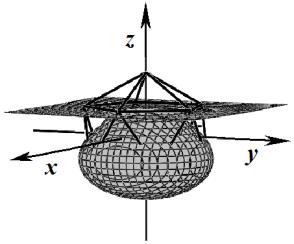
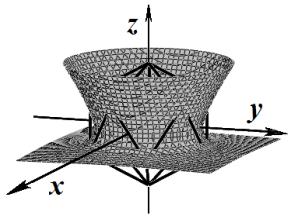
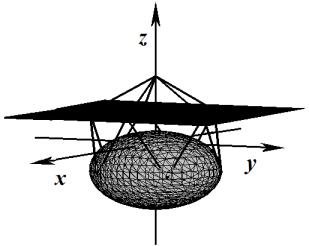
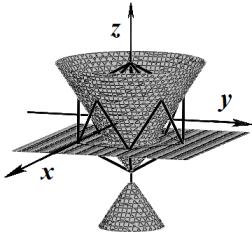
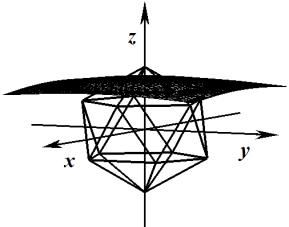
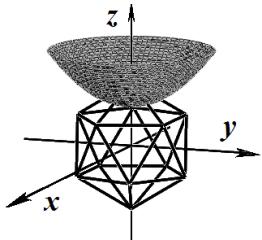
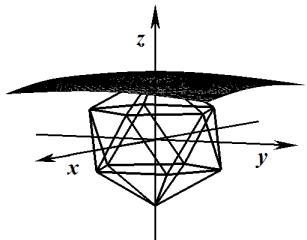
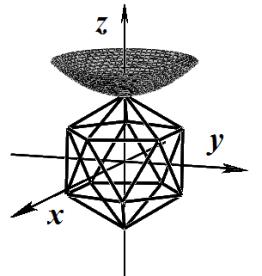
В результате решения систем (2-3) для функции (1) получаем два базиса икосаэдра (4) и (5). Графики поверхностей уровня для нескольких значений базисной функции представлены в табл. 1.

Таблица 1

Поверхности уровня базисной функции

Базис (4)	Базис (5)

Продолжение табл. 1

		(4)

		(5)

Выводы и перспективы дальнейших исследований. Все, рассмотренные авторами, базисы, учитывая предшествующие публикации [3-4], имеют матрицу Грама с одним и тем же числом обусловленности в норме метрики . В тоже время значения определителей матриц Грама для этих базисов различны. Их распределение представлено на рис. 2.

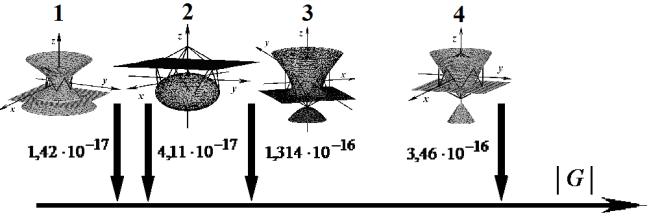
Рис. 2. Значения определителей матриц Грама для разных базисов икосаэдра:

1 — базис на основе комбинаций уравнений однополостного гиперболоида и плоскости [4]; 2 — базис (4); 3 — базис на основе гармонических поверхностей вращения третьего порядка [3]; 4 — базис (5).

Очевидно, что все рассмотренные базисы имеют практически равный положительный прогноз своих аппроксимационных качеств. Вопрос о приоритете должен решаться, исходя из условий конкретной задачи.

Литература

1. Березин И.С. Методы вычислений. Т. 1 / И.С. Березин, Н.П. Жидков. — М.: Наука, 1966. — 632 с.

2. Астионенко И.А. Серендиповы элементы: ретроспектива и современные концепции / И.А. Астионенко, А.Н. Хомченко // Проблемы информационных технологий. — 2009. — №1 (005). — С. 140—144.

3. Зычкова Е.Э. Гармонический базис икосаэдра на основе поверхностей вращения [Электронный ресурс] / Е.Э. Зычкова, А.П. Мотайло,
Г.Я. Тулученко, А.Н. Хомченко // Материалы VII Международной научно-практической конференции "Наука: теория и практика". Серия: Математика: Прикладная математика (7-15 августа 2011 г.). — Пшемысль, Польша: Sp. z o.o. "Nauka I studia", 2011. — Т. 9. Технические науки. Математика. Физика. Строительство и архитектура. Физкультура и спорт. — С. 67—73. — Режим доступа: http://www.rusnauka.com/Page_ru.htm.

4. Зычкова Е.Э. Геометрический подход к построению базиса икосаэдра: комбинация однополостного гиперболоида и плоскости [Электронный ресурс] / Е.Э. Зычкова, А.П. Мотайло, Г.Я. Тулученко, А.Н. Хомченко // Материалы VII Международной научно-практической конференции "Восточное партнерство". Серия: Математика: Прикладная математика (7-15 сентября 2011 г.). — Пшемысль, Польша: Sp. z o.o. "Nauka I studia", 2011. — Т. 10. Технические науки. Математика. Физика. Строительство и архитектура. Физкультура и спорт. — Режим доступа: http://www.rusnauka.com/Page_ru.htm.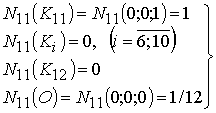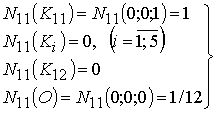