Математика/5. Математичне моделювання

Довгунь А.Я., д.ф.-м.н. Ясинський В.К.

Буковинська державна фінансова академія,

Чернівецький національний університет імені Юрія Федьковича,

Про Існування розв’язків стохастичних диференціальних рівнянь з післядією та інтегральними контракторами

Розглянемо на ймовірнісному базисі випадковий процес ,, зі значеннями в , -вимірний вінерів процес та центровану пуассонову міру з параметром . При справджуються наступні рівності

та

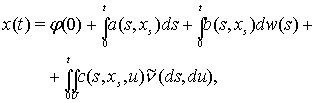(1)

при .

Тут ; ; , – матриця розмірності над простором ; , , – вимірні за сукупністю змінних; ; простір Скорохода неперервних справа функцій на відрізку , що мають лівосторонні границі [4], [5].

Тоді назвемо сильним розв'язком СДФР

(2)

з початковою умовою

(3)

У просторі для визначимо норму

. (4)

Нехай , , є обмеженими неперервними функціоналами. Для введемо випадковий процес

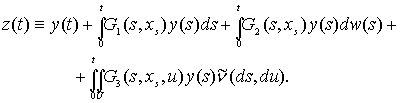(5)

Припустимо, що існує додатна стала така, що для всіх виконуються нерівності

(6)

(7)

(8)

майже скрізь відносно норми (2.4).

Означення 1. Якщо умови (6), (7) та (8) виконуються, то говорять, що коефіцієнти рівняння (2) мають обмежені інтегральні контрактори [6].

Означення 2. Обмежений випадковий контрактор є правильним, якщо рівняння (5) має розв'язок в для довільних i з .

Означення 3. Говорять, що функціонал є стохастично замкнений, якщо для довільних , з та , з таких, що , при i в , де для всіх майже скрізь.

Теорема 1. Якщо коефіцієнти в (2) є стохастично замкненими, мають обмежений випадковий інтегральний контрактор і для довільного існують інтеграли ; ; , то існує розв'язок задачі Коші (2), (5), (3).

Теорема 2. (про єдиність розв'язків СДФР). Нехай виконуються умови теореми 1 і обмежений випадковий контрактор для СДФР (2) є правильним. Тоді розв'язок задачі (2), (3), (5) є єдиним з точністю до стохастичної еквівалентності.

Зауваження 1. Якщо функціонали , , є ліпшицевими за другим аргументом, то вони є стохастично замкненими і мають правильний обмежений випадковий інтегральний контрактор з , [7].

Література:

1. Жакод Ж. Предельные теоремы для случайных процессов : в 2 т. / Ж. Жакод, А.Н. Ширяев. - М.: Физматгиз, 1994. – Т. 1. - 544 с.

2. Жакод Ж. Предельные теоремы для случайных процессов : в 2 т. / Ж. Жакод, А.Н. Ширяев. - М.: Физматгиз, 1994. – Т. 2. - 473 с.

3. Королюк В. С. Ймовірність, статистика та випадкові процеси. Теорія та комп’ютерна практика : у 3 т. Т. 3 : Випадкові процеси. Теорія та комп’ютерна практика / В. С. Королюк, Є. Ф. Царков, В. К. Ясинський. – Чернівці : Золоті литаври, 2009. – 798 с.

4. Гихман И. И. Стохастические дифференциальные уравнения и их применения / И. И. Гихман, А. В. Скороход. – К. : Наук. думка, 1982. – 612 с.

5. Биллингсли П. Сходимость вероятностных мер / П. Биллингсли. – М. : Наука, 1977. – 352 с.

6. Kuc H.H. On integral contractors / H.H. Kuc // Journal of Integral Equations. - 1979. - P.35 - 46.

7. Jankovich Sv. On stochastic differential-difference equations and their random integral contractors / Sv. Jankovich // Научные труды. - Том 562. - Математика. - Рига: Латвийский университет, 1991. - С. 74 - 84.