Технические науки/4. Транспорт

Д.т.н. Баламирзоев А.Г., инженер Баламирзоев Р.А.

Махачкалинский филиал МАДИ

Численные методы решения задач транспортного равновесия

Моделирование и исследование транспортных потоков часто проводится с помощью теории конкурентного бескоалиционного равновесия, описывающего достаточно адекватный механизм функционирования автомобильных улично-дорожных сетей (УДС). Рассматриваемые модели позволяют получить прогнозные оценки по загрузке элементов транспортной сети. Подобные задачи интересны в частности тем, что являются одним из инструментов для объективной оценки эффективности проектов по модификации УДС с точки зрения разгрузки наиболее проблемных участков дорог и уменьшения общих затрат на передвижение пользователей сети.

Эквивалентность задачи транспортного равновесия вариационному неравенству, а в частном случае оптимизационной задаче, позволяет адаптировать численные методы решения последних для поиска равновесных потоков.

К настоящему времени можно выделить два основных подхода к построению алгоритмических схем. В первом случае задачу транспортного равновесия моделируют только через потоковые переменные по дугам и, соответственно, поиск равновесия ведется по дугам сети (дуговые алгоритмы). Во втором - основной переменной задачи является поток по пути, соответственно, итерирование ведется по допустимым маршрутам (маршрутные алгоритмы). И в первом, и во втором случаях основная трудность при численных расчетах состоит в большой размерности решаемых задач, особенно на реальных транспортных сетях.

Богатый практический опыт накоплен для частного случая, когда транспортное равновесие ищется как решение оптимизационной задачи

.

Наиболее распространенным дуговым алгоритмом является метод Франка Вульфа [9], несмотря па то, что этот алгоритм имеет довольно медленную сходимость, существенно замедляющуюся при приближении к равновесию и весьма чувствительному к размерности задачи. Причиной такого поведения является как практически неизбежно вырождающийся характер вспомогательной задачи линейного программирования, так и неравномерная сходимость потоков к равновесным значениям или так называемый эффект «застревающих потоков» [5,7, 10] в процессе решения формируется некоторый набор дуг, по которым потоки сильно отличаются от равновесных, и такая ситуация не меняется при последующем итерировании.

Маршрутные алгоритмы распределяют корреспонденции непосредственно по множеству альтернативных путей, причем это множество, как правило, формируется в процессе решения [6, 12]. Перераспределение потоков не по дугам, а сразу по маршрутам, позволяет своевременно уйти от «застревающих потоков», поэтому алгоритмы данного класса не обладают отмеченным недостатком метода Франка Вульфа и сходятся равномерно, однако и здесь есть свои проблемы. Основная идея алгоритмов состоит в последовательной балансировке потоков между альтернативными маршрутами для каждой пары источник - сток. Поскольку перераспределение одного потока между маршрутами изменяет транспортные затраты во всей сети и тем самым влияет на распределение других корреспонденции, то возникает необходимость многократного просмотра всех потоко-образующих пар и повторения перераспределения потоков. Отсутствие необходимости априорного задания всех допустимых маршрутов для каждой пары источник - сток, с одной стороны, делает алгоритмы поиска равновесия по путям привлекательными для использования, с другой, - как показала вычислительная практика [5, 6], такие алгоритмы сводят к минимуму количество используемых путей, то есть теряется возможность равномерного расщепления корреспонденции по множеству привлекательных маршрутов.

Поиск транспортного равновесия как решения вариационного неравенства

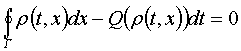(1)

исследован в основном теоретически, несмотря на то, что более адекватное моделирование транспортных потоков все-таки требует рассмотрения общего случая непотенциальной и/или неаддитивной функции затрат G(x) = (G_p(x) : р Î Р). В целом алгоритмический аппарат для вариационных неравенств разработай достаточно хорошо, о чем свидетельствуют монографии [8, 11], но большое количество переменных и сложное описание вектор-функции G(x) на практике делают задачу (1) труднорешаемой.

Среди существующих методов решения вариационных неравенств отдельно можно выделить проективные методы, отличающиеся простотой своих итерационных схем:

(2)

где проекция точки у на множество X. Для простых множеств (гиперплоскость, полупространство, шар, брус и т.п.) операция проектирования вычисляется аналитически, в общем случае требуется решать задачу квадратичного программирования, что значительно усложняет общий процесс. При выборе шага , , проективный метод сходится к равновесному распределению при весьма общих предположениях о свойствах задачи, однако на практике такой выбор ведет к очень медленной скорости сходимости.

Для декомпозиции и ускорения сходимости процесса (2) предполагается применить подходы, основанные на теории фейеровских процессов с малыми возмущениями [1, 2] с использованием адаптивной регулировки шага [3]. Основная идея этого подхода заключается в следующем. Допустимое множество X из (1) можно представить в виде пересечения конечного числа гиперплоскостей H_w и неотрицательного ортанта Н⁺:

,

где , . Объединим супермножества H_w и Н⁺ в семейство множеств H={H⁺,H_w:wÎW}= { H_l:l=1,2,… ½ W½+1}. Операция проектирования pH_l(^.) для любого элемента H_l вычисляется аналитически. Поэтому для численных расчетов транспортных потоков использовалась следующая модификация процесса (18), получившая название метода последовательных проекций [4]:

v_k=( p_Hl)/l_k (19)

H_lÎH, H_l, l_k>0, k=0, 1, 2, …

Значительного ускорения сходимости процесса (19) к равновесному решению удается достичь за счет адаптивного выбора шагового множителя l_k. Обозначим V(k_tm) = conv{v^k,v^k+1, ..., v^m} выпуклую оболочку векторов v^k,v^k+1, ..., v^m через B = {x : ||x|| ≤ 1} - единичный шар. Для заданной последовательности q®+0 при t®∞ определим последовательность индексов {k_t}. Шаговые множители l_k определялись по следующим правилам.

1. При t = 0 полагается k_t =0, l₀ > 0 - произвольное, q Î (0,1).

2. Для данных t и k определяется индекс k_t+1, такой, что

0 Ï V(k_t,s) + q_tB, l_s=l_{k t}, k_t≤s≤k_t+1, 0ÎV(k_t,k_t+1)+q_tB.

3. Положить .

4. Увеличить номер итерации t = t + 1 и повторить вычисление (19) для текущего значения l_k.

Другими словами, по условию п. 2 первый переход к шагу k_t+1 после k_t осуществляется тогда, когда при этом шаговый множитель уменьшается в q < 1 раз (п. 3).

Литература:

1. Луканин В.Н., Буслаев А. П., Трофимов Ю. В., Яшина М.В. Автотранспортные потоки и окружающая среда. М.: ИНФРА-М, Ч. 1, 2. 1998, 2001.
2. Кеrпеr В. S. Introduction to modem traffic flow theory and control. The long road to three - phase traffic theory. Springer, 2009.
3. Лакc П. Д. Гиперболические дифференциальные уравнения в частных производных. М.-Ижевск: НИЦ «РХД», IIKIL 2010.
4. Олейник О. А. Об одном классе разрывных решений квазилинейных уравнений первого порядка // Научные доклада высшей школы. Физико-математические науки. 1958. № 3. С. 91-98.
5. Гасников А. В. Сравнение определений обобщенного решения задачи Коши для квазилинейного уравнения. М.: ВЦ РАН, 2006.
6. Овсянников Л. В. Групповой анализ дифференциальных уравнений. М: Наука, 1993.
7. Кружков С. Н. Нелинейные уравнения с частными производными (Лекции). Ч. 2. Уравнения первого порядка. М.: Изд-во МГУ, 1970.
8. Эванс Л. К. Методы слабой сходимости для нелинейных уравнений с частными производными. Новосибирск: Тамара Рожковская (Белая серия в математике и физике; Т. 2), 2006.
9. Holden H., Risebro N. H. Front tracking for hyperbolic conservation laws. Springer. 2007.
10. Dafermos С. М. Hyperbolic conservation laws in continuum physics. Springer. 2010.
11. Ладыженская О. А., Солонников В. А., Уральцева Н. Н. Линейные и квазилинейные уравнения параболического типа. М.: Наука. 1967.
12. Субботин А. И. Обобщенные решения уравнений в частных производных. Перспективы динамической оптимизации. М.-Ижевск: НИЦ «РХД», ИКИ, 2003.