Явтушенко
Александр Викторович
Запорожский национальный технический университет,
Украина
Кинематический
анализ исполнительного восьмизвенного
механизма вытяжного пресса
Для выполнения операций глубокой вытяжки используются механические прессы со специальным исполнительным механизмом, обеспечивающим в период рабочего хода движение ползуна со скоростью, близкой к постоянной [1–4]. В современных конструкциях специализированных прессов наибольшее применение находят многозвенные рычажные механизмы, состоящие из нескольких простейших. Одним из таких механизмов является исполнительный восьмизвенный механизм, используемый в прессах фирм ”Hitachi ” (Япония), ”Schuler” (ФРГ) и др. Анализ структурной схемы механизма показывает необходимость всестороннего кинематического и динамического анализа с целью определения рациональной комбинации параметров, обеспечивающих удовлетворение технологических требований и определения области рационального использования.
Целью настоящей статьи является определение аналитических зависимостей для определения кинематических характеристик механизма, которые должны составить основу для последующего кинематического анализа и оптимизационного параметрического синтеза.
Главный исполнительный механизм вытяжного пресса представляет собой сочетание трех механизмов (рис. 1), первый из которых представляет собой обычный четырехзвенник кривошипного исполнения. К ведомому звену этого механизма (шарнир С) присоединена трехшарнирная двухзвенная диада, состоящая из рычагов CD и DE. Шарнир E звена DE расположен на ведущем кривошипе первого механизма. Таким образом, второй механизм представляет собой также четырехзвенник O2CDEO1 и имеет две степени подвижности W при 4 подвижных звеньях и 5 кинематических парах V класса
![]() .
.
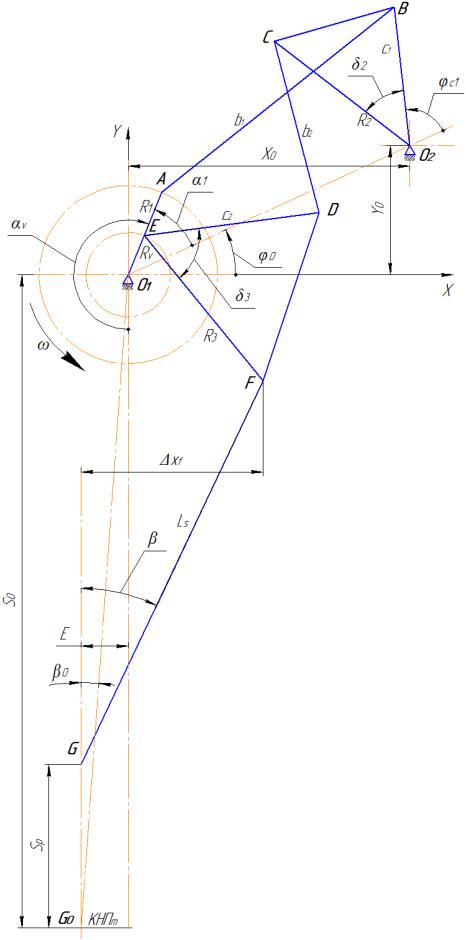
Рис. 1 – Расчетная схема механизма
Лишняя степень подвижности устраняется тем, что движение звена O1E задано для первого механизма и определено координатой α1.
Диада рычагов CD и DE через трехплечий рычаг DEF соединена с третьим механизмом, состоящим из шатуна FG и ползуна G, являющегося рабочим органом механизма. Кинематический эффект рассматриваемого механизма обеспечивается тем, что шарнир F совершает движение по специальной траектории и при определенных положениях механизма на рабочем участке поворота ведущего кривошипа O1A обеспечивается движение ползуна со скоростью, близкой к постоянной.
Координатой входного звена является угол поворота α1, отсчитываемый от положительного направления оси О1X1 против часовой стрелки. Координатой выходного звена является перемещение ползуна Sp, отсчитываемое от крайнего нижнего положения против движения ползуна. Вспомогательная ось О1X1 повернута относительно основной оси О1X на угол φ0. При анализе кинематики механических прессов угол отсчета поворота главного вала принимается от линии перемещения ползуна против движения кривошипа. В таком случае расчетный угол поворота кривошипа О1А определяется по формуле
![]() .
.
Кинематический анализ составного механизма рассматривается последовательно для каждого составляющего механизма. Все размеры звеньев механизма, в том числе и угловые, показанные на рис. 1, считаем заданными.
Анализ первого четырехзвенника рассмотрен в работе [5]. В системе координат X1О1Y1, когда ось X1 направлена по линии центров O1O2, угловые положения звеньев AB и O2B определяются зависимостями (рис. 2)
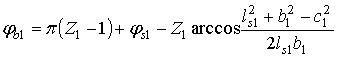 , (1)
, (1)
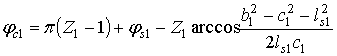 . (2)
. (2)
где Z1 – вариант сборки
механизма, в данном случае ![]() ;
;
φs1 – угол наклона отрезка АO2
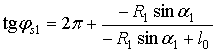 ;
;
ls1 – переменная длина отрезка АO2
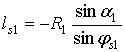 ;
;
l0 – расстояние между центрами O1 и O2.
При известном угловом положении звена O2B координата звена O2C определяется углом δ2
двухплечего рычага BO2C ![]() . Тогда координаты шарнира С в системе координат X1О1Y1
будут (рис. 2)
. Тогда координаты шарнира С в системе координат X1О1Y1
будут (рис. 2)
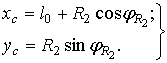 (3)
(3)
В той же системе координат положение точки шарнира Е определяется как
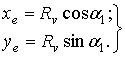 (4)
(4)
Из треугольника CDE при известных координатах шарниров C и E и известных размерах рычагов CD и DE находим
![]() .
.
По теореме косинусов определяются значения углов γ и ψ
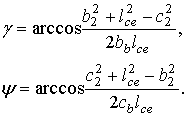
Тогда значения углов φc2 и φb2, определяющих положения звеньев CD и DE будут
![]() ;
;
![]() .
.
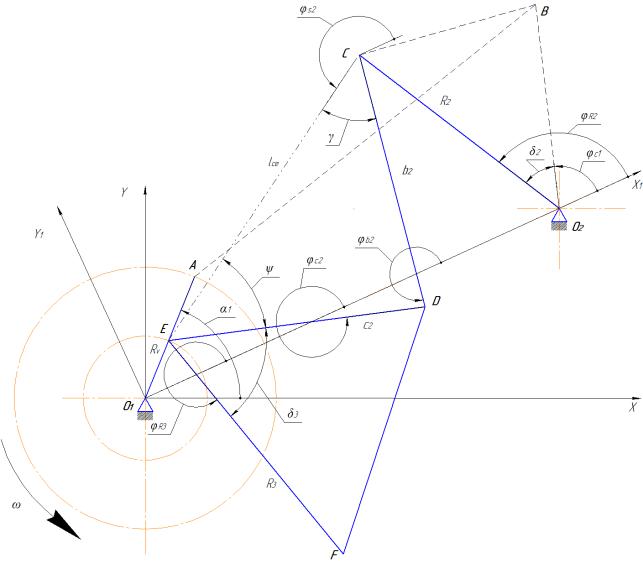
Рис. 2 – Расчетная схема 2-го механизма
Здесь φS2 – угол наклона линии AC относительно оси X1
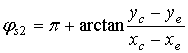 .
.
Таким образом, координаты точек шарниров D и F будут
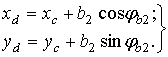
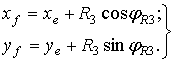 (5)
(5)
Угол φR3 для
рычага EF определяется как ![]() .
.
При известных координатах точки шарнира F функция положения третьего механизма определяется в основной системе координат XO1Y, принятой при анализе кинематики механических прессов. Направление перемещения ползуна Sp определяется от его крайнего нижнего положения (точка G0), а угол поворота αv ведущего кривошипа – от вертикальной оси, проходящей через центр шарнира О1 против его движения
![]() . (6)
. (6)
Координаты точки F представляються в основной системе координат
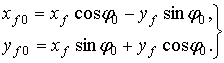 (7)
(7)
Система уравнений (7) представляет собой параметрическое уравнение шатунной кривой, описываемой точкой F.
Угол наклона β шатуна определяется как
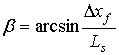 , (8)
, (8)
где ∆xf – смещение точки F по оси O1X
![]() .
.
Дезаксиал Е принимается с соответствующим знаком. При смещении линии движения ползуна в направлении вращения главного вала дезаксиал принимается положительным, в противном случае, как показано на рис. 1 – отрицательным.
Перемещение ползуна, являющееся функцией положения механизма, определяется как
![]() , (9)
, (9)
где S0 – расстояние точки крайнего нижнего положения от оси O1X
![]() ;
;
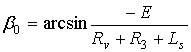 .
.
Передаточные функции механизма представляют собой первую и вторую производные функции положения (9) по координате α1 ведущего звена
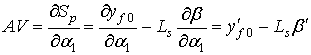 . (10)
. (10)
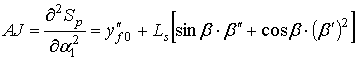 . (11)
. (11)
Здесь и далее штрихами обозначены соответственно первая и вторая производные переменных по координате α1.
Производные переменных по координате α1 определяются дифференцированием соответствующих
выражений в уравнениях (7), (5) и (4) с учетом того, что ![]() , находим
, находим
![]()
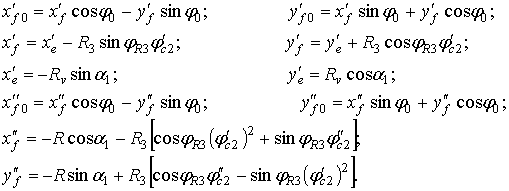
Для определения первой передаточной функции ![]() второго механизма
рассмотрим векторный многоугольник O1EDCO2, показанный на рис. 3.
Векторное условие замкнутости механизма
записывается в виде
второго механизма
рассмотрим векторный многоугольник O1EDCO2, показанный на рис. 3.
Векторное условие замкнутости механизма
записывается в виде
![]() .
.
Проекция многоугольника на ось O1X1 будет
![]() .
.
Дифференцируя полученное уравнение, находим
![]() . (12)
. (12)
Вычитая угол φb2 из всех углов в полученном выражении, что
равнозначно повороту осей координат на угол -φb2, и учитывая, что
![]() находим
находим
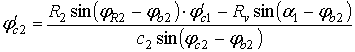 .
.
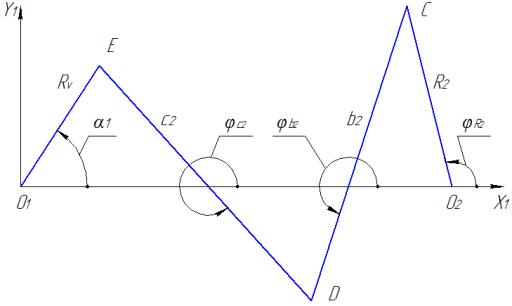
Рис. 3 – Векторный многоугольник 2-го механизма
Аналогично, вычитая угол
φс2,
находим зависимость для определения переменной ![]() , необходимой для определения второй передаточной функции
механизма
, необходимой для определения второй передаточной функции
механизма
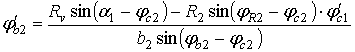 .
.
Производные ![]() и
и ![]() , представляющие собой первые передаточные функции первого
механизма определяются аналогичным образом [5]
, представляющие собой первые передаточные функции первого
механизма определяются аналогичным образом [5]
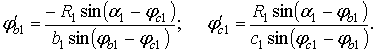
Вторая передаточная функция ![]() второго механизма
определяется после повторного дифференцирования выражения (12) и вычитания угла
φb2
второго механизма
определяется после повторного дифференцирования выражения (12) и вычитания угла
φb2
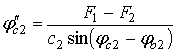 ,
,
где
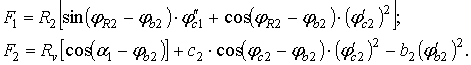
Первая производная угла β определяется дифференцированием выражения (8). Первое дифференцирование дает
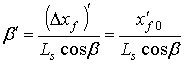 .
.
Дифференцируя дважды выражение (8), получим
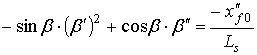 ,
,
откуда находим
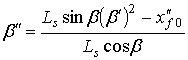 .
.
Производные угла β определяются после двукратного дифференцирования выражения (8) по координате α1
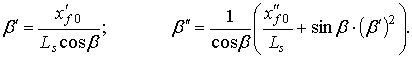
Зависимости (9), (10) и (11) однозначно определяют
кинематические характеристики механизма в зависимости от его геометрических
параметров, дают возможность оценки его свойств и служат теоретической основой
для оптимизационного параметрического синтеза.
Фактические значения скорости Vp и ускорения Jp ползуна находятся из зависимостей, определяющих
понятие передаточных функций. Если скорость кривошипа ![]() принять
постоянной, то тогда получим
принять
постоянной, то тогда получим
![]() (13)
(13)
![]() (14)
(14)
В качестве примера на рисунке 4 показаны результаты расчета кинематических параметров восьмизвенного механизма вытяжного пресса номинальным усилием 8 МН. Угловая скорость ω кривошипа принята равной 1 рад/с.
Для сравнения на рисунке приведена первая передаточная функция дезаксиального кривошипно-ползунного механизма (показаны штриховыми линиями и обозначенными индексом ”k”) имеющего такой же максимальный ход ползуна (810 мм) и такой же дезаксиал (-200 мм), что и механизм рассматриваемого пресса. Из рисунка следует, что при принятых параметрах механизма обеспечивается основное функциональное назначение механизма, как исполнительного органа пресса для глубокой вытяжки – на участке рабочего хода обеспечивается практически постоянная скорость движения ползуна. Если принять, что рабочий ход ползуна составляет примерно 200 мм, то из рисунка следует, что скорость начала рабочего хода рассматриваемого механизма (примерно 160 мм/с) более чем в два раза меньше скорости ползуна кривошипно-ползунного механизма (примерно 380 мм/с) и сохраняется практически неизменной на 2/3 участка рабочего хода. Скорость обратного хода ползуна незначительно превышает скорость ползуна кривошипно-ползунного механизма. Отрицательным явлением является увеличение ускорения ползуна при обратном ходе, однако учитывая, что величина максимального ускорения не превышает 800…900 мм/с2, при качественном изготовлении механизма это обстоятельство не является недостатком механизма.
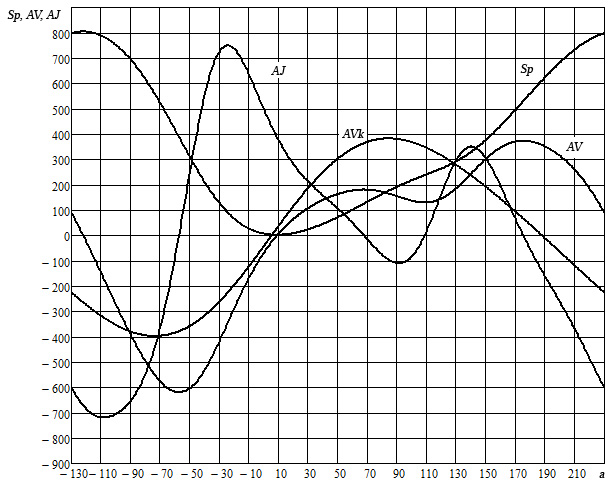
Рис. 4 – Кинематические характеристики вытяжного пресса
номинальным усилием 8 МН
Из анализа характера изменения скорости ползуна следует
важное преимущество анализируемого механизма. Из условия равенства мгновенной
мощности на ведущем и ведомом звене
идеального механизма следует, что величина движущего крутящего момента Мкр пропорциональна первой передаточной функции
механизма ![]() и усилию деформации Рд
и усилию деформации Рд
![]() .
.
Отсюда следует, что при одном и том же усилии деформации, действующим на ползун, величина необходимого крутящего момента пропорциональна скорости ползуна. Тогда в рассматриваемом механизме крутящий момент будет в несколько раз меньше, чем в кривошипно-ползунном механизме, следовательно, соответствующим образом уменьшаются нагрузки на детали и узлы привода, что способствует снижению металлоемкости и стоимости пресса в целом.
Выводы
1. Восьмизвенный исполнительный механизм вытяжного пресса соответствует функциональному назначению и полностью удовлетворяет технологические требования в отношении скорости перемещения ползуна в период рабочего хода.
2. Представленные аналитические зависимости определяют все кинематические характеристики механизма в зависимости от его параметров, дают возможность анализа влияния параметров и служат основой для последующего параметрического синтеза механизма.
3. Рассматриваемый механизм обеспечивает снижение скорости в период рабочего хода по сравнению с кривошипно-ползунным механизмом более чем в два раза. При оптимальном выборе параметров обеспечивается уменьшение скорости начала рабочего хода с последующим ее незначительным возрастанием в процессе деформации.
4. Сопоставление рассматриваемого механизма с механизмами других структурных схем, например, с шестизвенными механизмами прессов фирм ”Aida ” (Япония), ”Clearing” (США) и др., показывает, что при примерно одинаковом характере изменения скорости ползуна в период рабочего хода он имеет более сложную конструкцию, следовательно, менее технологичен и более металлоемкий.
Список использованной литературы
1. Живов Л.И. Кузнечно-штамповочное оборудование: Учебник для вузов / Л.И. Живов, А.Г. Овчинников, Е.Н. Складчиков / Под ред. Л.И. Живова. – М.: Изд-во МГТУ, 2006. – 560 с.
2. Бочаров Ю.А. Кузнечно-штамповочное оборудование: Учебник для вузов / Ю.А. Бочаров. – М.: Издательский центр «Академия», 2008. – 480 с.
3. Свистунов В.Е. Кузнечно-штамповочное оборудование. Кривошипные прессы / В.Е. Свистунов. – М.: МГИУ, 2008. – 704 с.
4. Műller S. Gesichtspunkte
fűr die Gestaltung von Kurbel- und Tiefziehpressen // Maschinenbautechnik,
21, 1972, № 4. p. 170-174.
5. Явтушенко А.В. Кинематика многозвенного прижимного механизма механических прессов / А.В. Явтушенко, А.В. Явтушенко, Т.А. Васильченко // Современная техника и технологии. – Март 2014. - № 3 [Электронный ресурс]. URL:http://technology.snauka.ru/2014/03/3324 (дата обращения: 17.03.2014).