Алюков А.С.

Южно-Уральский государственный университет, Челябинск, Россия

Моделирование динамики колесной платформы

в компьютерной среде Matlab/Simulink

Новое поколение робототехнических систем характеризуется повышенной мобильностью, активным взаимодействием с внешней средой, расширенными способностями приспособления к сложному, неопределенному и подвижному окружению. Высокие качественные характеристики и подвижность так называемых активных роботов используется для выполнения целого ряда нетривиальных операций, таких как обход препятствий, проникновение в труднодоступные зоны, выбор удачного подхода к внешним объектам и прецизионное движение по сложным криволинейным трассам с сохранением требуемой ориентации в пространству [1-3]. Мобильность активных роботов, приспосабливаемость к внешней среде и сравнительная автономность делает их использование весьма привлекательным для самых разнообразных сфер человеческой деятельность, включая автоматизированное производство, космос и подводные исследования, оборону, медицину и т.д.

Рассматриваемая колесная платформа имеет два ведущих колеса. Ведомые (пассивные) колеса можно исключить из рассмотрения. Схема платформы с принятыми обозначениями изображена на рис.1.

Здесь:

x, y – абсолютная земная система координат;

X,Y – связанная система координат;

геометрический центр платформы с координатами (;

центр масс платформы с коориднатами

референтная точка платформы с координатами ;

b – расстояние от ведущего колеса до оси симметрии;

r – радиус ведущих колес;

масса платформы без учета массы ведущих колес;

масса каждого ведущего колеса;

момент инерции платформы без учета ведущих колес относительно вертикальной оси, проходящей через центр масс;

момент инерции каждого ведущего колеса относительно оси колес;

момент инерции каждого ведущего колеса относительно диаметра колеса;

a – длина платформы;

d – расстояние по оси X от точки до точки .

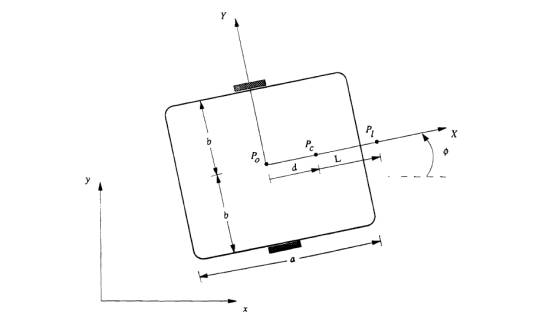
Рис.1. Схема колесной платформы

Разработка и анализ регуляторов для модели в пространстве состояний изучена и описана во многих литературных источниках. Для записи уравнения состояния необходимо определиться с выбором вектора состояния – вектора, элементами которого являются переменные состояния. Для рассматриваемой системы можно записать вектор состояния как

Используя данные переменные состояния, уравнение движения платформы можно записать так

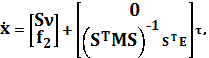(1)

где .

Система уравнений состояния (1), описывающая движение колесной платформы, была смоделирована в среде Matlab/Simulink. Модель платформы в Simulink представляет собой блок Dynamics. Вид данного блока приведен на рис.2.

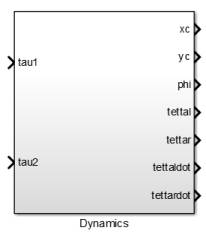
Рис.2. Модель колесной платформы в Simulink

Блок имеет два входа – tau1 и tau2. Данные входы – моменты, создаваемые электродвигателями на левом и правом ведущем колесе соответственно. Выходами блока являются 7 переменных состояния. Структура блока приведена в Приложении таком-то. Вычисление значений матриц S, M, V, E реализовано с использованием m-функций. На вход блоков подаются аргументы, необходимые для вычисления значений матрицы. Выходом каждой функции является блок Goto с соответствующим именем. Вид данных блоков в среде Simulink представлен на рис.3.

В данной работе нелинейная динамическая система в итоге приводится к так называемому цепному квазиканоническому виду. Для этого, предварительно, необходимо получить аффинную систему уравнений:

(2)

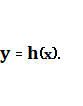(3)

Система «вход-состояние-выход» вида (2), (3) называется аффинной или линейной по управлению. Таким образом, возникает задача привести математическую модель объекта к виду (2) и выбрать уравнения выхода (3).

Рис.3. Функции для вычисления матриц S, M, E, V

Если для системы (1) в качестве управляющего воздействия τ выбрать

(4)

где символ + обозначает псевдоинверсию, уравнение (1) приводится к виду (2). Здесь

Выражение (4) может упрощаться в конкретных случаях. Для рассматриваемой конструкции двухколесной платформы выражение принимает вид

Литература:

1. Бурдаков С.Ф., Мирошник И.В., Стельмаков Р.Э. Системы управления движением колесных роботов. – СПб.: Наука, 2001. – 229 с.

2. Алюков А.С. Совершенствование конструкции динамически стабилизируемых робототехнических систем на основе сферического колеса. Материалы VIII Международной научно-практической конференции "Образование и наука в XXI веке". – Том 48. Технологии. – София, Болгария: "Бял ГРАД-БГ" ООД. – 2012. – С. 64-67.

3. Nilanjan Sarka, Xiaoping Yun, R. Vijay Kumar. Control of Mechanical System with Rolling Constraints: Application To Dynamic Control of Mobile Robots. – University of Pennsylvania,1992. – 28 p.