Кайнарбеков А.К., Танирбергенов А.К.

Гуманитарный университет транспорта и права им. Д.А.Кунаева,

г Алматы, Республика Казахстан

ШАГАЮЩЕЕ КОЛЕСО «СКОЛЬЗЯЩИЙ КАБЛУК»

Второе предложение также направлено на то, чтобы добиться плавности хода и устранения ударного приземления спиц шагающего колеса, не прибегая к усложнению его конструкции. Смысл идеи заключается в следующем: падение спицы колеса спустить по наклонной плоскости, путем установки на пятку каблука, скользящего вдоль спицы.

Возникла необходимость теоретического анализа работы этого колеса.

Были построены в масштабе схема колеса и повернутого на небольшой угол φ₁ положение спицы 2. На чертеже повернутое положение колеса показано тонкими линиями (рис. 1а и 1в).

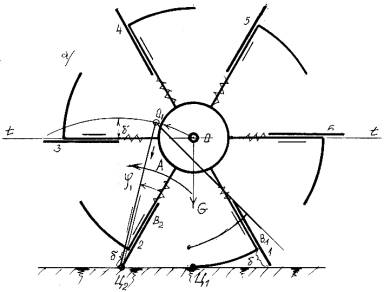
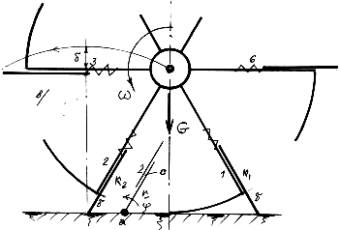
Рисунок 1. Шагающее колесо на скользящем каблуке

Это предложение требует проверки, но есть надежда на успех его осуществления.

Был изготовлен макет предлагаемого шагающего колеса (рисунок 2а и рис. 2б), который показал хорошие результаты: достигнута плавность хода и устранено ударное приземление наступающей на поверхность дороги спицы.

Рисунок 1

Это было видно визуально как на макете, так и на построенных схемах положений колеса. Следовательно, при переходе центра масс на другую спицу колесо остается на одной опоре Ц₂. Тогда спица 2 (рисунок 1в), удерживая вес колеса G, падает вдоль своего каблука как бы по наклонной плоскости. В этот момент механизм спицы обладает двумя степенями подвижности:

W=3n – 2p₁ = 3∙2 – 2∙2 = 2,

где n=2 – число подвижных звеньев (ступица 2 с корпусом и каблук К),

р₁=2 – число кинематических пар 5 класса (одноподвижные шарниры а и с).

Эти схемы показали, что переход центра масс к наступающей спице 2 происходит мгновенно, так как при повороте даже на малый угол φ₁ с опоры отрывается задняя спица 1.

Одной подвижностью управляет привод колеса, а другой управляет проекция силы веса. Это означает, что перемещение ступицы колеса не однозначно зависит от угла поворота спиц φ₁. Спуск колеса по наклонному скользящему каблуку зависит не только от φ₁, но и от других факторов. Время спуска зависит от величины значения силы веса G, а также от коэффициента силы трения f_с между материалами спицы и каблука. Становится ясным, что в данном случае не может быть достигнута прямолинейность траектории центра ступицы О колеса.

Рисунок 2б

После этого анализа можно утверждать, что для выполнения требования о плавности хода шагающего колеса необходимо, чтобы в процессе выполнения одного шага колеса перевод центра тяжести происходил стоя на двух спицах. При этом указанный процесс шагания осуществляется на двух скользящих каблуках (впредь будем называть их штангами).

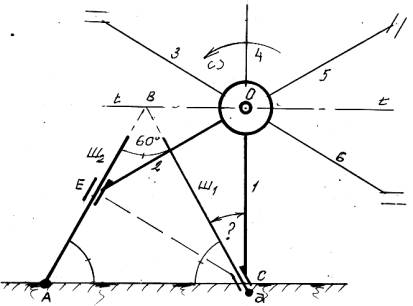
Рисунок 3. К синтезу схемы ШК «скользящий каблук»

Теперь надо точно определить угол наклона штанг к направлению спиц и убрать ступни спиц колеса (рисунок 3). Учтем, что две смежные спицы образуют механизм, степень подвижности которого равна

W=3n – 2p₁ = 3∙3 – 2∙4 = 1,

где n=3 – (штанги Щ₁ и Щ₂ и корпус ступицы), р₁=4 – (две опорные точки штанг А и а и направляющие Е и С корпуса ступицы, скользящие вдоль штанг).

Это значит положение центра ступицы О при перекатывании зависит только от угла поворота спиц.

ЛИТЕРАТУРА

1. Муратов А. М., Кайнарбеков А. К., Сазанбаева Р. И., Антонова Ж.Ж. Синтез схемы шагающего колеса. - Алматы: 2007г.

2. Муратов А. М., Сазанбаева Р.И., Мусин Т.О. Синтез строения замкнутых кинематических цепей без избыточной связи. // Вестник. КазАТК., №5, 2001г.

3. Муратов А.М., Кайнарбеков А.К. Синтез схемы исполнительного механизма 4-го класса.// «Промышленный транспорт Казахстана» -. Алматы: КУПС, № 5, 2007г.

4. Муратов А. М. Докторская диссертация. «Синтез многофункциональных механизмов высоких классов» - Алма-Ата: 1986г. С.230.