Математика/4. Прикладная математика

Аспирант Бобков А.С. , к.б.н. Артеменко М.В.

Юго-западный государственный университет

ЭКСТРАПОЛЯЦИЯ СОСТОЯНИЯ ОБЪЕКТОВ НА ОСНОВЕ МЕТОДА ГРУППОВОГО УЧЕТА АРГУМЕНТОВ

Задача прогнозирования поведения исследуемого объекта во времени и пространстве заключается к экстраполяции регистрируемых значений определенных характеризующих наблюдаемых параметров на заданный промежуток времени. Для имитационного эксперимента идентифицируются модели, отражающие изменения во времени значений упомянутых факторов в виде формализованного функционала от определенного набора аргументов. Существует проблема выбора метода синтеза адекватных моделей в условиях коротких временных рядов большого множества параметров и принадлежности их значений некоторым нечетким множествам и различным законам распределения. Для ее разрешения предлагается применять нечеткие алгоритмы структурно-параметрической идентификации экстраполяционных моделей на основе метода группового учета аргументов (МГУА), родоначальником которого является Ивахненко А.Г. [1].

Алгоритмы МГУА позволяют идентифицировать зависимость любой структурной сложности в условиях статистически незначимой выборке полученной в результате мониторингования, когда число неизвестных параметров модели больше количества «точек» (измеренного вектора значений факторов в зафиксированный момент времени в зафиксированной точке факторного пространства).

Поскольку полином Колмогорова-Габора в качестве экстраполянта, представляется в виде ,то применяются многорядные алгоритмы МГУА по методике, изложенной в [2]. Заметим, однако, что в данном случае возникает вероятность пропуска приемлемой модели в процессе селекции (хотя и существенно сокращается время вычислительного процесса).

Для случая, когда экстраполируемая функция зависит от множества факторов , т. е. (где определяет уровень запаздывания фактора), в работе [3] предлагается применять алгоритмы МГУА с последовательным выделением временных трендов.

Методология построения подобных алгоритмов заключается в следующем. Допустим, необходима структурно-параметрическая идентификация модели . На первом шаге алгоритма осуществляется ранжирование множества по корреляционному отношению к эктраполяционной функции . Определяется тренд 1-го порядка , в котором: - переменная наиболее корректируется с . Функции идентифицируются алгоритмами МГУА. Для определения тренда второго порядка определяется разность и аналогичный отрезок идентифицирует тренд второго порядка . Синтез модели продолжается до достижения приемлемого значения определенного критерия.

Применение концепции самоорганизационного моделирования в алгоритмах МГУА позволяет достигнуть необходимой точности прогностической модели, однако возникают альтернативы выбора критерия «остановки» работы алгоритма поскольку, в случае применения относительных критериев работа алгоритма может продолжаться бесконечно долго.

В связи с указанными проблемами идентификации моделей предлагается применять нечеткий метод группового учета аргументов.

В этом случае структурно-парметрический синтез алгебраических моделей осуществляется путем применения линейных интервальных регрессионных моделей вида (2).

(2),

где - характеризующая состояние объекта значение фактора (или значения функции частных моделей предыдущих рядов селекции), - интервалы, определяющие нечеткими числами с треугольными функциями принадлежностями согласно, например, формуле (3).

(3),

где - центр, - ширина интервала.

Значения Y в этом случае рассчитывается по формуле (4).

(4),

интервалы определяются неравенствами 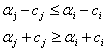(5).

(5).

Поскольку, регистрируемые (наблюдаемые) значения множества включаются в определенный оценочный интервал с минимальной «шириной», то задача поиска параметров (коэффициентов модели) может быть решена с помощью классических алгоритмов линейного программирования.

Литература

1. Бояринов Ю.Г., Стоянова О.В., Дли М.И. Нейро-нечеткий метод группового учета аргументов для поддержки принятия решений по управлению региональными социально-экономическими системами. -М.:Физматлит,2005,-168 с.

2. Ивахненко А.Г., Степашко В.С. Помехоустойчивость моделирования.- Киев: "Наук. думка", 1985. - 216 с.

3. Proceedings of International Workshop on Inductive Modelling (IWIM 2007). - Prague: Czech Technical University, 2007. - 329 p.