С. А. Оганисян, Л. М.
Буниатян
Государственный
инженерный университет Армении
Проектирование системы управления
робота-манипулятора типа SCARA на основе
теории количественной обратной связи
В статье предлагается методика проектирования
системы управления робота-манипулятора (РМ) типа SCARA [1] с двумя степенями
свободы на основе теории количественной
обратной связи (КОС) [2, 3] и метода характеристических передаточных функций
(ХПФ) [4], примененного к линеаризованным уравнениям движения РМ.
РМ типа SCARA (рис. 1) является одним
из видов роботов, который широко используется в промышленности для сборки
изделий, пайки и так далее. Для простоты, в работе рассматриваются только первые
два вращательных звена РМ, как это показано на рис. 2.
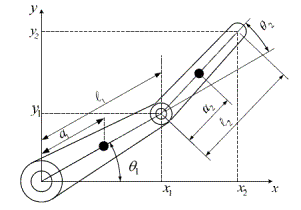
Рис. 1 Робот SCARA Рис. 2 Модель робота SCARA
Для проектирования двумерной взаимосвязаннной системы
управления РМ воспользуемся теорией КОС. Последняя основана на частотных
представлениях и позволяет обеспечить требуемые показатели качества и запасы
устойчивости замкнутой системы при наличии параметрических неопределенностей в
объекте регулирования. Теория КОС широко применяется при проектировании систем
с одним входом и выходом (одномерных систем) и основана на использовании
диаграмм Никольса [3].
Рассмотрим систему управления РМ на рис. 2,
матричная структурная схема которой представлена на рис. 3.
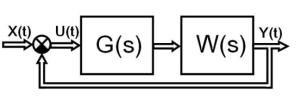
Рис. 3 Обшая структурная схема РМ
На рис. 3: 
, 
и 
- двумерные векторы входа, ошибки и выхода, 
- 
передаточная матрица
регулятора, 
- 
передаточная матрица линеаризованного объекта
регулирования (робота-манипулятора).
Будем считать, что матрица 
неопределена и
имеет вид:
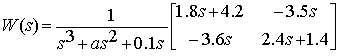, (1)
где
неопределенный параметр 
принадлежит области 
Применив метод ХПФ [4], передаточную матрицу 
(1) можно представить
в следующем каноническом виде:
, (2)
где через
обозначены ХПФ разомкнутой системы, а
модальная матрица 
составлена из линейно-независимых собственных
векторов матрицы 
.
С помощью ХПФ 
-мерная система может быть представлена как совокупность 
независимых одномерных
систем, к которым можно применить теорию КОС с использованием диаграмм Никольса.
Ставится следующая задача: выбрать регулятор 
так, чтобы взаимосвязанная замкнутая система
управления РМ была устойчивой, а её показатель колебательности по отношению к вектору
выхода не превышал значение 
.
Для решения данной задачи следует построить на
диаграмме Никольса запретную окружность для заданнного значения 
и характеристические годографы разомкнутой
системы при граничных значения 
и 
. Для устойчивости системы необходимо, чтобы годографы не
охватывали критическую точку (-180, 0) и находились вне запретной окружности 
. На рис. 4 на плоскости
диаграммы Никольса построены характеристические годографы 
матрицы 
(2) и запретная окружность при 
. Так как годографы 
охватывают точку
(-180, 0), то это значит, что система неустойчива и, естественно, требуемое значение 
не удовлетворяется.
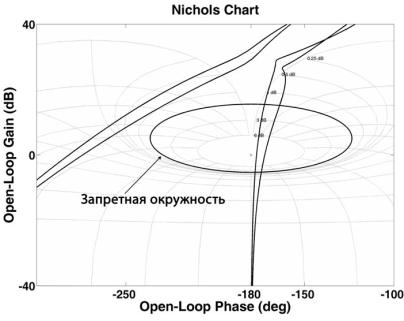
Рис. 4 Характеристические годографы исходной системы и
запретная
окружность на плоскости диаграммы Никольса
Для обеспечения устойчивости и показателей
качества вводим в систему регулятор 
,
передаточная матрица которого имеет следующий вид:
. (3)
На рис. 5 показаны характеристические годографы скорректированной
системы и запретная окружность для 
. Как видно из рис. 5, годографы находятся вне зоны окружности. Это значит, что
взаимосвязанная система управления РМ устойчива и удовлетворяется значение 
.
Выводы. С помощью приведенной
методики, основанной на совместном использовании теории КОС и метода ХПФ, была
спроектирована система управления РМ, где выбранный регулятор обеспечивает
устойчивость и качественные характеристики замкнутой системы. Рассмотренный подход
применим к многомерным системам любой размерности.
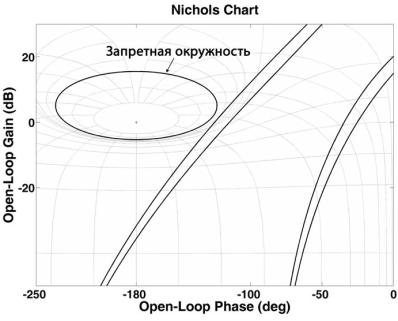
Рис. 5 Характеристические годографы скорректированной системы
и
запретная окружность 
на плоскости диаграммы
Никольса
Литература
1. Khongsomboun, K., Benjanarasuth, T., Komine, N.: IMC-Based PID
Controllers Design for a Two-Links SCARA Robot. IEEE Region 10 Conference, 1030
– 1034, TENCON (2011).
2. Isaac Horowitz, Invited paper Survey of quantitative feedback theory
(QFT), INT.J, CONTROL, 1991, vol. 53, No. 2, 255-291.
3. Constantine H. Houpis, Steven J. Rasmussen, Quantitative feedback theory: fundamentals and applications,
1999 by Marcel Dekker, Inc.
4. Гаспарян О.Н., Теория многосвязных систем автоматического
регулирования, ГИУА, Изд.-во “Асогик”, Ереван, 2010.