Технические науки / 4. Транспорт

Неженцев А.Б., Аветисян С.М., Гонтарь Д.В.

Восточноукраинский национальный университет им. В.Даля

Динамические нагрузки при передвижении мостовых кранов с частотным управлением

Уже не возникает сомнений в том, что наиболее перспективным по динамическим и энергетическим характеристикам крановым электроприводом является частотно-управляемый электропривод. В настоящее время на рынке предлагается много частотных преобразователей с различными схемными решениями и законами частотного управления асинхронными электродвигателями. На их базе разрабатываются системы автоматического управления крановыми электроприводами с высокими показателями плавности, энергоэффективности и диапазоном регулирования скорости.

Вместе с тем, анализ переходных процессов мостовых кранов с частотным управлением электроприводов передвижения показал, что в зависимости от изменения таких факторов как время работы частотного преобразователя (T_P), шаг изменения частоты (h_ч), диапазон регулирования частоты напряжения статора (f₁) параметры процесса разгона крана (горизонтальные динамические нагрузки на металлоконструкцию крана S_м и груз S_к, а также время разгона крана t_р) могут как значительно снижаться, так и существенно возрастать.

Цель работы - построение уравнений регрессии, аппроксимирующих максимальные динамические нагрузки S_м и S_к, а также время разгона t_р мостового крана г/п 10 т при частотно-регулируемом пуске.

Мостовой кран рассматривался в виде трехмассовой динамической модели, движение которой описывается нелинейными дифференциальными уравнениями второго порядка [1]. При этом приведенная к ходовым колесам сила электропривода передвижения крана с частотным управлением (с учетом зависимости момента двигателя М от фазного напряжения статора , частоты f и скольжения s) задавалась по выражению, приведенному в работе [2].

Уровни и интервалы варьирования факторов T_P, h_ч, f₁ для мостового крана грузоподъемностью 10 т приведены в табл. 1.

Таблица 1 - Уровни и интервалы варьирования факторов T_P, h_ч, f₁

Уровни факторов	ТР, с	hЧ, Гц	f1, Гц
Код (zi)	z1	z2	z3
Основной уровень (zi = 0)	3,0	1,5	42,5
Интервал варьирования (Dzi)	1,0	1,0	7,5
Верхний уровень (zi = +1)	4,0	2,5	50,0
Нижний уровень (zi = -1)	2,0	0,5	35,0

Уравнения регрессии для параметров S_м, S_к, t_р построены в виде полиномов второго порядка:

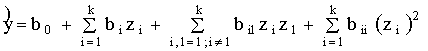, (1)

где - оценка аппроксимируемого параметра; , , - коэффициенты регрессии; k - число факторов.

Для проведения компьютерного эксперимента использовали квази-D-оптимальный план типа [3], представляющим собой план второго порядка, построенный на гиперкубе k-й размерности, имеющим равное число опытов в вершинах куба и центрах (k-1)-мерных граней. В каждой точке плана (при определенном сочетании факторов T_P, h_ч, f₁) решалась система нелинейных дифференциальных уравнений второго порядка [1] численным методом Рунге-Кутта с помощью программы (в среде Delphi) [4]. При этом на каждом шаге интегрирования определялись максимальные значения динамических нагрузок на металлоконструкцию крана S_м и груз S_к, которые принимались за результаты опыта в данной точке плана.

Матрица плана и результаты компьютерного эксперимента для динамических нагрузок S_м в металлоконструкции мостового крана г/п 10 т приведены в табл. 2. В графах 5-7 показаны натуральные значения варьируемых факторов, а в графах 8-10 приведены: результаты компьютерного эксперимента S_м, расчетные (по уравнению регрессии) значения и их разность ΔS_м.

Таблица 2 – Динамические нагрузки S_м в металлоконструкции
мостового крана г/п 10 т при разгоне с частотным управлением

№	z1	z2	z3	ТР, с	hч, Гц	f1, Гц	Sм, кН	, кН	ΔSм, кН
1	2	3	4	5	6	7	8	9	10
1	1	1	1	4	2,5	50	8,297	8,214	0,083
2	-1	1	1	2	2,5	50	6,993	7,064	-0,071
3	1	-1	1	4	0,5	50	5,903	6,001	-0,098
4	-1	-1	1	2	0,5	50	6,355	6,482	-0,127
5	1	1	-1	4	2,5	35	7,765	7,689	0,076
6	-1	1	-1	2	2,5	35	7,416	7,369	0,047
7	1	-1	-1	4	0,5	35	5,569	5,475	0,094
8	-1	-1	-1	2	0,5	35	6,727	6,787	-0,060
9	1	0	0	4	1,5	42,5	7,486	7,641	-0,155
10	-1	0	0	2	1,5	42,5	7,934	7,722	0,212
11	0	1	0	3	2,5	42,5	7,658	7,793	-0,135
12	0	-1	0	3	0,5	42,5	6,586	6,395	0,191
13	0	0	1	3	1,5	50	6,932	6,719	0,213
14	0	0	-1	3	1,5	35	6,452	6,609	-0,157
15	0	0	0	3	1,5	42,5	7,164	7,277	-0,113

По методу наименьших квадратов (реализованного в стандартных программах) были рассчитаны коэффициенты уравнения регрессии для расчета и исследования динамических нагрузок S_м при разгоне мостового крана г/п 10 т с частотным управлением электропривода передвижения:

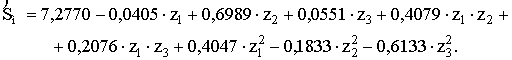(2)

Аналогично были получены уравнения регрессии для расчета динамических нагрузок S_к и времени разгона t_р мостового крана г/п 10 т:

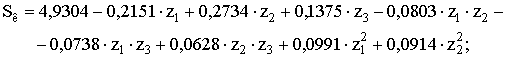(3)

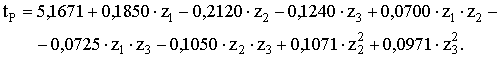(4)

Поскольку адекватность полученных в результате компьютерного эксперимента (дисперсия опыта равна нулю) уравнений регрессии (2 - 4) невозможно проверить по критерию Фишера, то проверка адекватности осуществлялась с помощью коэффициента вариации

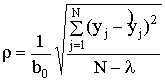, (5)

где N – число опытов; λ – число коэффициентов уравнения регрессии.

Уравнения регрессии (2 - 4) оказались адекватными, так как .

Выводы: Полученные полиномы (2 - 4) пригодны для расчета S_м, S_к и при любых значениях факторов в исследованной области их определения. При этом точность расчета такая же, как и при решении дифференциальных уравнений. Уравнения регрессии позволяют не только исследовать влияние каждого фактора и их взаимодействий на величину максимальных динамических нагрузок S_м, S_к и время разгона мостового крана г/п 10 т с частотным управлением, но и решать задачи выбора наиболее экономичных по динамическим нагрузкам и быстродействию законов частотного управления.

Литература

1. Будиков Л.Я., Нгуен Н.К., Неженцев А.Б. Исследование динамики грузоподъемных кранов // Вестник машиностроения, №4. - М.: Изд-во Машиностроение, 1981, - С. 39-42.

2. Неженцев А.Б., Аветисян С.М. Математическая модель приведенной силы кранового электропривода с частотным управлением // Материали за 7-а международна научна практична конференция, «Образованието и науката на ХХІ век». - Том 17. Технологии. Здание и архитектура. - София: «Бял Град-БГ» ООД, 2011. – С. 58-60.

3. Таблицы планов эксперимента для факторных и полиномиальных моделей / Под ред. В.В. Налимова. – М.: Металлургия, 1982. – 752с.

4. Аветисян С.М., Неженцев А.Б. Программное обеспечение для исследования переходных процессов грузоподъемных кранов (ч. 1: при работе механизмов передвижения) // Підйомно-транспортна техніка, №4(8). - Днепропетровск, 2003. – с. 33-48.