Технические науки 5. Энергетика

Федоров В.К., Пестрикова И.Е., Пестрикова Л.Е., Лопатина Л.Г.,

Панарина И.В., Тарзанова Н.С.

Омский государственный технический университет, Россия

Обоснование возможности возникновения

хаотических режимов в электронных цепях.

Идентификация хаотических и переходных

хаотических колебаний

Бифуркация странного аттрактора может осуществляться как переход типа «хаос-хаос» или «хаос-порядок». Бифуркация странного аттрактора может быть вызвана сменой «устойчивости» нетривиальных гиперболических подмножеств, которые, будучи непритягивающими при значениях параметров ниже точек бифуркации, порождают метастабильный хаос. Метастабильная стохастичность наблюдается конечное время вместе со «стабильным» хаосом исследуемого хаотического режима, а с превышением параметров бифуркационных значений гиперболическое подмножество в окрестности исходного аттрактора становится притягивающим. Фиксируется бифуркационный переход типа «хаос-хаос».

Рассмотрим бифуркацию рождения квазиаттрактора из аттрактора Лоренца, реализующуюся в известной модели Лоренца [1]

, , .

Методом численного эксперимента с использованием строгих результатов установлены границы области существования аттрактора Лоренца на плоскости параметров r и для b = 8/3.

Обратимся к рис.1, где приведены соответствующие бифуркационные кривые. Кривая l₁ отвечает существованию двоякоасимптотической негрубой траектории типа петли седлового состояния равновесия в нуле координат. Кривая l₂ характеризует бифуркацию рождения аттрактора Лоренца. Заштрихованная область значений параметров отвечает условиям существования негрубого аттрактора Лоренца. Бифуркационная кривая l₃ разделяет пространство параметров НЭЦ на области существования аттрактора Лоренца и квазиаттрактора.

Пересечение этой линии вызывает бифуркационный переход «хаос-хаос», при котором аттрактор Лоренца разрушается, уступая место квазиаттрактору. В области квазиаттракторов сохраняется сложная структура разбиения фазового пространства на траектории, включающие и гомоклинические. Однако появляются негрубые гомоклинические траектории седловых циклов и, как следствие, – устойчивые периодические движения с большими периодами и малыми областями притяжения.

Точка бифуркации странного аттрактора – это негрубое состояние нелинейной электронной цепи (НЕЦ) в момент прохождения одного из ЛХП через нулевое значение в критической точке. Например, для некоторого сигнатура спектра ЛХП аттрактора была «+», «0», «-», …, «-».

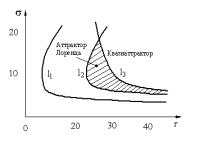
Рис. 1. Бифуркационная диаграмма перехода типа «хаос - хаос» в аттракторе Лоренца [1]

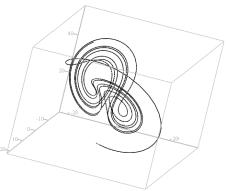
Рис. 2. Трехмерное изображение аттрактора Лоренца,

построенное путем численного моделирования в среде MathCAD

В бифуркационной точке третий показатель спектра обращается в нуль, отражая негрубость режима: «+», «0», «0», «-», …, «-», и с превышением появляется грубый аттрактор с другой сигнатурой спектра ЛХП: «+», «+», «0», «-», …, «-».

Переходы в хаосе сопровождаются изменениями размерности и с физической точки зрения соответствуют вовлечению в колебательный процесс новых степеней свободы. Ввиду резкого замедления скорости сходимости ляпуновских показателей вблизи критической точки достоверно диагностируется лишь грубая ситуация, сопровождаемая «скачком»: «+», «0», «-», …, «-» «+», «+», «0», «-» , …, «-».

Бифуркация указывает, что хаотический режим связан с потерей устойчивости [2]. Описание условий бифуркации подразумевает точный способ описания точки бифуркации, в которой изменение параметра приводит к потере устойчивости. В точке бифуркации существование и единственность решений не обеспечивается, и происходит изменение числа решений.

В основном были классифицированы следующие задачи неустойчивости состояний в дифференциально-алгебраической модели НЭЦ [3]:

(1) Тип I – рабочий режим, при котором переменные состояния и параметры НЭЦ ограничены в пределах приемлемых условий работы,

(2) Тип IIA – алгебраическая бифуркация, возникающая из-за наличия функциональной зависимости, связанной с уравнениями баланса мощностей в НЭЦ,

(3) Тип IIS – статическая бифуркация, возникающая вследствие сингулярности эквивалентной матрицы Якоби НЭЦ, при условии несингулярности матрицы Якоби электрической сети,

(4) Тип IID – динамическая бифуркация, возникающая в результате неустойчивых колебаний,

(5) Тип III – проблема каскадной устойчивости из-за неточной согласованности регулировок НЭЦ.

Бифуркации седловой точки – особый, но, несмотря на это, общий случай статической бифуркации, когда эквивалентная матрица Якоби НЭЦ имеет простое нулевое собственное значение; бифуркация Хопфа – особый, но, несмотря на это, общий случай динамической бифуркации, когда эта матрица имеет пару чисто мнимых собственных значений

Обнаружение хаоса может быть реализовано путем введения показателей Ляпунова. Показатели Ляпунова хаотической траектории имеют, по крайней мере, одну положительную величину λ. Так, самый большой показатель Ляпунова λ₁ должен быть положительным. Эта характеристика отличает хаос от других типов установившихся режимов.

Используя множество показателей Ляпунова, мы можем рассмотреть переходный хаос более тщательным образом.

На данном интервале характеристические показатели Ляпунова, определены как: .

Переходные колебания, как упоминалось, образует переходный хаос на всем интервале тогда и только тогда, когда оно имеет по крайней мере одну положительную величину . Из определения , следует, что, если колебание хаотическое, оно должно быть переходным хаотическим колебанием. Однако обратная формулировка, в общем случае, не является истинной.

Переходные хаотические колебания имеют характеристики широкополосного энергетического спектра и непредсказуемости на интервале , так как эти свойства – прямые следствия наличия положительных значений показателей Ляпунова, которые объясняют чрезвычайную чувствительность к начальным условиям.

Преимущество использования показателей Ляпунова заключается в том, что в случае динамической неустойчивости удобно вычислить показатели Ляпунова для малого интервала , чтобы изучить природу переходного колебания.

Литература:

1. Курдюмов, С. П. Синэнергетика – теория самоорганизации / С. П. Курдюмов, Г. Г. Малинецкий. – М.: Знание, 1983. – 63 с.

2. Розенвассер, Е. Н. Колебания нелинейных систем. – М.: Наука, 1969. – 576 с.

3. Харкевич, А. А. Спектры и анализ. – М.: Гостехиздат. – 1957. – 334 с.