Сухина Микола Сергійович

Національний технічний університет України

“Київський політехнічний інститут імені Ігоря Сікорського”

Аналіз канонічного алгоритму Хаффмана стиснення веб-даних

Анотація: в даній статті розглядаються математичні основи канонічного алгоритму Хаффмана, виконується кодування послідовності символів та на основі отриманих результатів проводиться оцінка ефективності даного алгоритму.

Ключові слова: веб-додаток, інтернет, веб-сторінка, алгоритм Хаффмана, стиснення даних, оптимізація, підвищення швидкодії роботи веб-додатку.

Вступ

В наш час інтернет розвивається швидкими темпами, а разом із ним і веб-додатки. Сьогодні майже кожне підприємство, фірма чи державний заклад мають свій власний веб-сайт, на якому розміщують різну інформацію. Більшість людей здійснюють купівлю різних пристроїв та інших речей онлайн, використовуючи свої віртуальні гаманці чи здійснюючи переказ коштів з кредитних карток.   Існують онлайн карти, які дозволяють прокласти маршрут в будь-яке потрібне нам місце. При цьому ми можемо вибрати вид транспорту, отримати розклад руху маршруток та час, який необхідний, щоб дістатися до потрібного нам місця. Інтернет став невід’ємною частиною нашого життя.

Разом із швидкими темпами розвитку інтернету розвиваються і вимоги до веб-додатків. Вони отримують красивий дизайн з яскравими високоякісними картинками та навіть відео, яке відображається на задньому фоні сайту. У веб-додатках намагаються створити якомога більше динамічних елементів, що забезпечують зміну контенту сайту без перезавантаження веб-сторінки. Все це виконується для залучення користувачі до використання того чи іншого веб-додатку. В результаті на веб-сайтах розміщується велика кількість інформації, яка знижує швидкодію їх роботи, тому важливу увагу приділяють їх оптимізації.

Для підвищення швидкодії роботи веб-додатку виконують наступні дії:

·        мінімізація css та javascript файлів, яка полягає у видаленні всіх коментарів, переносів рядків та символів табуляції.

·        використання кешу браузера – при переході в певний веб-додаток відбувається завантаження великої кількості файлів, які браузер може зберігати в своєму кеші. При подальшому переході по сторінках даного веб-додатку деякі файли будуть зберігатися в кеші браузера і він не буде витрачати час на їх завантаження.

·        оптимізація зображень, яка полягає у їх стисненні певним методом.

·        стиснення текстових файлів, що дозволяє в 95-98% скоротити час на передачу файла браузеру.

Кожний із наведених шляхів оптимізації має важливе значення в підвищенні швидкодії роботи веб-додатку. Розглянемо метод стиснення даних за алгоритмом Хаффмана, який в наш час у комбінації з іншими алгоритмами активно використовується.

Алгоритм Хаффмана

Даний алгоритм для стиснення даних використовує частоту появи однакових байтів у вхідному блоці даних. Його особливість полягає в тому, що символи вхідного потоку, частота появи яких найбільша, кодуються послідовністю бітів найменшої довжини.

Введемо деякі визначення для розуміння роботи алгоритму.

Нехай заданий алфавіт який складається із кінцевої кількості букв. Кінцеву послідовність символів із 

будемо називати словом в алфавіті , а число n  – довжиною слова . Довжина позначається як .

Нехай заданий алфавіт Через  позначимо слово в алфавіті , а через – множину всіх непустих слів в алфавіті .

Нехай – множина всіх непустих слів в алфавіті  і  - деяка підмножина множини S . Нехай також задано відображення F , яке кожному слову  ставить у відповідність слово

Слово   будемо називати кодом повідомлення , а перехід від слова   до його коду – кодуванням.

Розглянемо відповідність між буквами алфавіту   і деякими словами алфавіту  :

Дана відповідність називається схемою і позначається символом  . Вона визначається наступним чином: кожному слову із ставиться відповідне слово , що називається кодом слова . Слова  називаються елементарними кодами. Даний вид кодування називається алфавітним кодуванням.

Нехай слово має вигляд

Тоді слово називається початком або префіксом слова  , а  - кінцем слова .

Схема  має властивість префікса, якщо для будь-яких i та j слово не є префіксом слова . В такому разі, якщо схема  має властивість префікса, то алфавітне кодування буде взаємно-однозначним.

Припустимо, що заданий алфавіт  і набір імовірностей появи символів . Нехай заданий  алфавіт Тоді можна побудувати цілий ряд ∑ схем  алфавітного кодування, що володіють властивістю взаємної однозначності.

Для кожної схеми можна знайти середню довжину  , яка визначається як математичне очікування довжини елементарного коду:

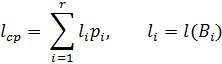
Довжина  показує, в скільки разів збільшиться середня довжина слова при кодуванні за допомогою схеми .

Можна показати, що  досягає величини свого мінімуму  на деякій схемі  і визначається як:

Коди, що визначені схемою  з  називаються кодами з мінімальною надлишковістю або кодами Хаффмана.

Застосування алгоритму Хаффмана

Нехай  задає символи вхідного потоку, а алфавіт                складається всього із нуля та одиниці.

Припустимо, що ми маємо 4 букви в алфавіті  та наступний розподіл імовірносте  

Здійснимо послідовно побудову схеми:

1.   Запишемо всі букви вхідного алфавіту у порядку спадання імовірностей частоти появи букви:

2.     Здійснимо об’єднання двох символів та   з найменшими імовірностями, видалимо з нашого списку дані елементи та на їх місці запишемо  псевдо елемент   .

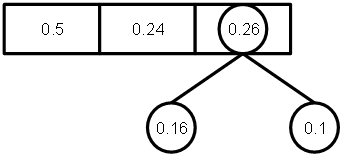
3.     Знову виконуємо крок 2

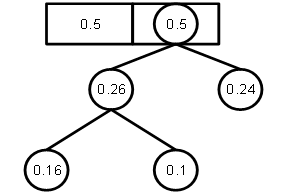
4.     Виконуємо крок 2 і після отримання дерева проходимося по ньому і для кожного переходу добавляємо 0, якщо ми йдемо вліво, і 1 – якщо ми йдемо вправо. В результаті отримаємо наступне бінарне дерево:

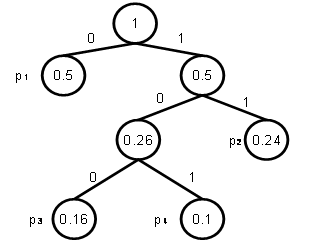
Маємо, для символу з ймовірністю   отримаємо , для   отримаємо ,  отримаємо ,  отримаємо . Отримані результати відповідають наступній схемі:

Дана схема представляє собою код Хаффмана.

Візьмемо послідовність із 100 символів. Кожний символ займає 8 біт, вся послідовність буде займати   біт. Нехай в даній послідовності символ  зустрічається 50 разів, символ  – 24 раз, символ  – 16 раз, символ  – 10 раз. Із застосування алгоритму кодування Хаффмана ми отримаємо послідовність із 176 біт  . Тобто в середньому на один символ витратимо 1.76 біта.

Висновок

У наш час в інтернеті розміщується велика кількість інформації, завдяки чому постає нагальна потреба в стисненні даних для підвищення швидкодії роботи веб-додатків. Стиснення даних за алгоритмом Хаффмана дозволяє значно скоротити розмір файлів. Проаналізувавши результати, можемо переконатися, що, наприклад, послідовність із 100 символів буде займати 800 біт, а з використанням алгоритму Хаффмана всього лише 176 біт. На даний момент одні із кращих алгоритмів – Brotliта Deflate використовують алгоритм Хаффмана у комбінації з алгоритмом LZ77 для стиснення даних.

Література:

1.     Методы сжатия данных. Устройство архиваторов, сжатие изображений и видео/[Ватолин Д., Ратушняк А., Смирнов М., Юкин В.]. –М.: Диалог-Мифи, 2003. – 384с

2.     Brotli — новый алгоритм сжатия веб-данных от Google [Електронний ресурс] – Режим доступу до ресурсу: https://habrahabr.ru/company/ua-hosting/blog/267533/.

3.     Топ-10 советов о том, как увеличить скорость загрузки страницы [Електронний ресурс] – Режим доступу до ресурсу: https://habrahabr.ru/post/137239/.

4.     Алгоритм Хаффмана на пальцах [Електронний ресурс] – Режим доступу до ресурсу: https://habrahabr.ru/post/144200/.