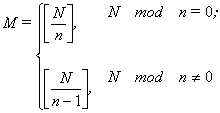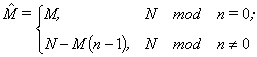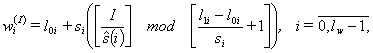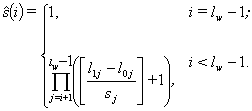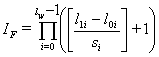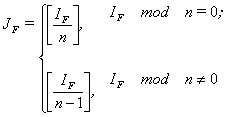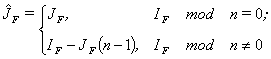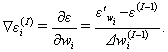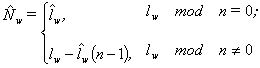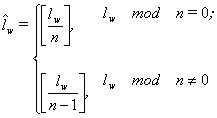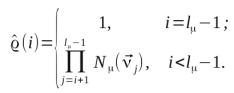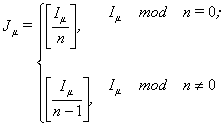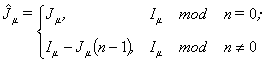P.h.D. Kryuchin O.V.

Tambov State University named after G.R. Derzhavin

The development of parallel algorithms training artificial neural networks

This paper aim is to develop parallel algorithms of the artificial neural network (ANN) training. Main task of it is to minimize target function

, (1)

where is the input pattern row, is the output pattern row, is the ANN output value calculation function, is the weight coefficients vector, is the activation functions vector, is the pattern row number and is the ANN output neurons number. This training consists of three levels (the structure training, the neurons activation functions training and the weight coefficients training) [1].

It is possibly to develop parallel algorithm of the training on each level. And it is possible to develop the parallel training on the level of the target function value calculation. If there are n processors and the pattern consists of N rows then each processor can calculate an inaccuracy by part of pattern (formula

(2)

for processor number k and formula

(3)

for zero (lead) processor). Then zero processor summands it

(4)

So the lead processor sends

	(5)

lines to all non-zero processors, calculates inaccuracy by

	(6)

rows, receives inaccuracies from other processor and calculates result [2].

There are different methods for the weight coefficients training level. Each method uses the unique parallel training. For example the parallel full enumeration method searches all variants of weight coefficients values. So i-th weight coefficient at I-th iteration is calculated by formula

	(7)

where

	(8)

The method does

	(9)

iterations. Here s_i is the i-th weight coefficient scanning step and l_w is the weights number. If there are n processors then each nonzero processors does

	(10)

iterations and the lead processor does

	(11)

iterations [3].

In parallel Monte-Carlo method weight coefficients are initiated by random values. In each iteration all processors generate a point in the weight coefficients point around and calculates inaccuracy for it. Then zero processor chooses the minimum inaccuracy. If this inaccuracy less than current inaccuracy then new coefficients will be set to a network [1, 3].

Gradient methods base on calculating the gradient vector and changing values of weight coefficients in the opposite direction

	(12)

It is the general idea but different gradient methods (for example QuickProp and RPROP) can use other semblable formulas.

In this algorithms the weights vector is divided to n parts and each part locates on different processor [3]. The lead processor calculates

	(13)

weight coefficients and other processors calculate

	(14)

gradient elements and weights.

As we know the universal mathematics neuron consists of two part. These are the adder and the activation function. An adder calculates amount of products input signal values to weight coefficients. So a neuron has several searching parameters (two impulse, activation function coefficient and type of activation function; several types of functions need some other parameters).

The activation function training is searching all these parameters. It needs full scanning all variant. It is symbolize possible values of i-th activation neural function as and size of this vector as . Thus it will be

	(6)

iterations and the i-th neuron activation function value at I-th iteration is calculated by formula

	(7)

where

	(8)

If there are n processors then each nonzero processor executes

	(9)

iterations and lead processor executes

	(10)

iterations.

Usually the first structure is minimal and then new neurons and layers are appended. The lead processor builds structure and sends it to free processor and this processor begins to search activation functions and weight coefficients. After the training finish processor sends structure to zero processor and receives new structure. This process continues until stop constraint will be executed.

So in this work parallel methods training ANN were developed.

Literature

1. Kryuchin O.V., Arzamastsev A.A., Troitzsch K.G. A universal simulator based on artificial neural networks for computer clusters [Электронный ресурс] — Электрон. дан. // Arbeitsberichte aus dem Fachbereich Informatik Nr. 2/2011. Koblenz. 2011. 13 p. — http://www.uni-koblenz.de/~fb4reports/2011/2011_02_Arbeitsberichte.pdf

2. Крючин О.В. Algorithms of artificial neural network teaching using the parallel target function calculation // Вестник Тамбовского Университета. Серия: Естественные и технические науки, - Т. 17, Вып. 3 – С. 981-985.

3. Oleg V. Kryuchin, Alexander A. Arzamastsev, Prof. Dr. Klaus G. Troitzsch (2011): A parallel algorithm for selecting activation functions of an artificial network, Arbeitsberichte aus dem Fachbereich Informatik, 12/2011, Universität Koblenz-Landau, ISSN (Online) 1864-0850 http://www.uni-koblenz.de/~fb4reports/2011/2011_12_Arbeitsberichte.pdf.