P.h.D. Kryuchin O.V.
Tambov State University named after G.R. Derzhavin
Numerical experiments for artificial neural network parallel training
efficiency analysis
We know that artificial neural networks
(ANN) are used in different science branches. But its usage needs long time expense
because neural network models have the large structure and many parameters. The
possible solution is the parallel algorithms and computer clusters usage. It
described in papers [1-4]. The aim of this work is to develop numerical
experiments for check of efficiency of these algorithms.
As we know the main task of neural network
training is to minimize the target function
(1)
where 
is the input pattern row, 
is the output pattern row, 
is the ANN output value calculation function,
is the weight coefficients vector, 
is the activation functions vector, 
is pattern row number and 
is the ANN output neurons number [1].
If serial the training algorithm elapses 
hours then ideal
parallel algorithm time expense is 
calculated by
formula
, (2)
where 
is the processors
number. But it is impossible
because the synergetic effect is able in particular occurrences only. So real
time expense of the parallel training is calculated by formula
. (3)
Here 
is the time
expense for prepare and sending data. So the efficiency coefficient may be calculated by formula
, (4)
where 
, 
are time expense
of serial and parallel algorithms and 
is the processors
number.
The first experiment is
forecasting the mass of caught shrimp. This experiment uses a multilayer
perceptron. Pic. 1 shows the obtained ANN structure and pic. 2 shows the
empirical and predicted values of shrimp mass. The efficiency coefficient values
can be found in table 1.
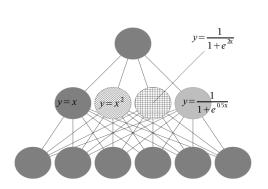
Pic. 1. ANN structure in forecasting of caught shrimp mass.
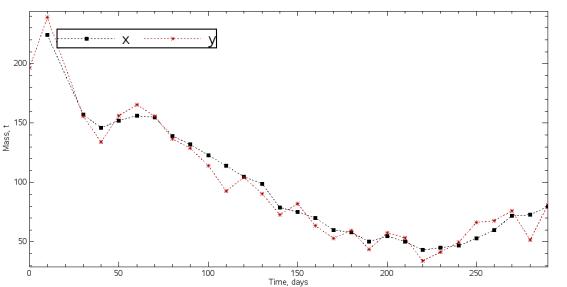
Pic. 2. Practical (x) and forecast (y) values of caught
shrimp mass.
Tab. 1. Efficiency coefficients for forecasting the
caught shrimp mass.
|
|
Cluster TSU |
Cluster TSTU |
Cluster MCC |
|
|
0.9235 |
0.9199 |
0.9297 |
|
|
0.9221 |
0.9157 |
0.9291 |
|
|
0.9204 |
0.9105 |
0.9283 |
|
|
0.8921 |
0.8822 |
0.9091 |
|
|
0.8906 |
0.8793 |
0.9079 |
|
|
0.8891 |
0.8769 |
0.9067 |
The second experiment is forecasting the air temperature
in Tambov (Russia). The values are shown in pic. 4, the structure is shown in
pic. 3, and efficiency coefficients are shown in table 2 [2].
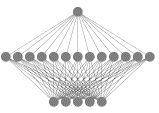
Pic. 3. ANN structure in forecasting of the air temperature.
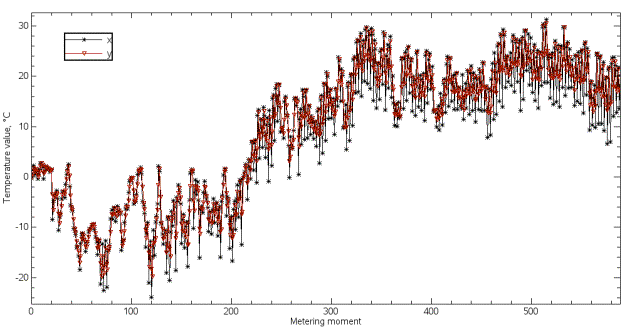
Pic. 4. Empirical (x) and forecast (y) values of
the air temperature.
Tab. 2. Efficiency coefficients for the air
temperature.
|
|
Cluster TSU |
Cluster TSTU |
Cluster MCC |
|
|
0.9312 |
0.9287 |
0.9401 |
|
|
0.9304 |
0.9273 |
0.9393 |
|
|
0.9297 |
0.9259 |
0.9387 |
|
|
0.9124 |
0.8974 |
0.9199 |
|
|
0.9112 |
0.8951 |
0.9182 |
|
|
0.9103 |
0.8936 |
0.9169 |
The third experiment is the forecasting of
exchange rates between Euro and US dollar. This experiment uses a multilayer
perceptron (MLP) and a Volterry network [3]. Values are shown in pic. 5, the
MLP-structure is shown in pic. 6, and coefficients of efficiency are shown in
table 3.
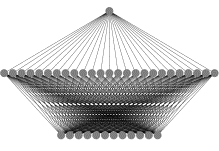
Pic. 5. ANN structure in forecasting of exchange
rates.
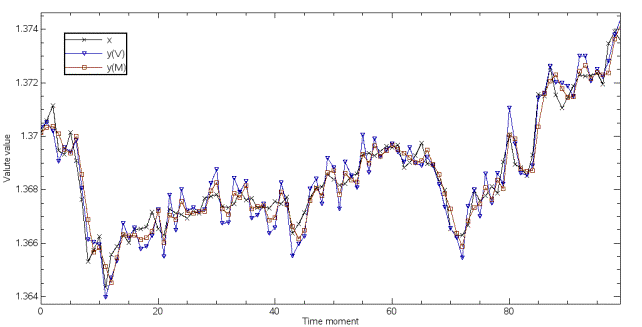
Pic. 6. Empirical exchange rates (x), exchange
rates forecast by multilayer perceptron (y(M)) and by Volterry (y(V)).
Tab. 3. Efficiency coefficients for the air
temperature.
|
|
Cluster TSU |
Cluster TSTU |
Cluster MCC |
|
|
0.9319 |
0.9281 |
0.9438 |
|
|
0.9302 |
0.9271 |
0.9392 |
|
|
0.9293 |
0.9261 |
0.9389 |
|
|
0.9127 |
0.8975 |
0.9202 |
|
|
0.9111 |
0.8949 |
0.9181 |
|
|
0.9101 |
0.8932 |
0.9165 |
The last experiment is social object simulation.
Social object here is the dependence of schoolboys' professional ability on
their personal characteristics [4]. Efficiency coefficients are shown in table 4.
Tab. 4. Coefficient of efficiency values for the
experiment of social object simulation.
|
|
Cluster TSU |
Cluster TSTU |
Cluster MCC |
|
|
0.9212 |
0.9103 |
0.9396 |
|
|
0.9212 |
0.9103 |
0.9391 |
|
|
0.9211 |
0.9098 |
0.9373 |
|
|
0.9129 |
0.8977 |
0.9205 |
|
|
0.9114 |
0.8951 |
0.9188 |
|
|
0.9103 |
0.8935 |
0.9169 |
So the numerical experiments for check the efficiency
of artificial neural network training algorithms were done.
References
1.
Kryuchin O.V.,
Arzamastsev A.A., Troitzsch K.G. A universal simulator based on artificial
neural networks for computer clusters [Ýëåêòðîííûé ðåñóðñ] — Ýëåêòðîí. äàí. //
Arbeitsberichte aus dem Fachbereich Informatik Nr. 2/2011. Koblenz. 2011. 13 p.
— http://www.uni-koblenz.de/~fb4reports/2011/2011_02_Arbeitsberichte.pdf
2.
Êðþ÷èí Î.Â., Êîçàäàåâ À.Ñ., Ñëåòêîâ Ä.Â., Àðçàìàñöåâ À.À. Òåñòèðîâàíèå
ïàðàëëåëüíûõ àëãîðèòìîâ îáó÷åíèÿ èñêóññòâåííûõ íåéðîííûõ ñåòåé íà ïðèìåðå ïðîãíîçèðîâàíèÿ
òåìïåðàòóðû âîçäóõà â ãîðîäå Òàìáîâå // Âåñòí. Òàìá. óí-òà. Ñåð. Åñòåñòâ. è òåõí.
íàóêè. 2011. – Ò. 16, Âûï. 2 – Ñ. 461-467..
3.
Oleg V. Kryuchin,
Alexander A. Arzamastev, Prof. Dr. Klaus G. Troitzsch, Natalia A. Zenkova
(2011): Simulating social objects with an artificial neural network using a
computer cluster, Arbeitsberichte aus dem Fachbereich Informatik, 15/2011,
Universität Koblenz-Landau, ISSN (Online) 1864-0850.
http://www.uni-koblenz.de/~fb4reports/2011/2011_15_Arbeitsberichte.pdf.
4.
Kryuchin O.V.,
Arzamastsev A.A., Troitzsch K.G. The prediction of currency exchange rates
using artificial neural networks [Ýëåêòðîííûé ðåñóðñ] — Ýëåêòðîí. äàí. //
Arbeitsberichte aus dem Fachbereich Informatik Nr. 4/2011. Koblenz. 2011. 12 p.
— http://www.uni-koblenz.de/%7Efb4reports/2011/2011_04_Arbeitsberichte.pdf